- •1. Числ ряды
- •2.Действия над рядами Св-ва
- •3. Необх признак сх
- •6. Ряды с неотр Признаки сравнения
- •7. Признак Даламбера.
- •3) В случае ответа о сходимости или расходимости ряда теорема не дает.
- •9. Интегральный признак Коши.
- •10.Знакпер ряд абс и услвн сх
- •12. Знакчеред ряды Лейбниц
- •14. Функ ряды область сх
- •15. Равн сх фр Вейерштрассе
- •17. Степ ряд Абель
- •25. Решение ду
- •27 Тригон ряд фурье
- •32. Разлож непериод функ
- •33. Тригоно ряд фурье в комп форме
- •34. Интеграл фурье
- •35 Комп форма инт фурье
- •36. Опред фкп
- •37. Предел и непрерывн фкп
- •42. Общая степен
- •43. Условие коши-риманна
- •47. Основн теор коши
- •48. Интегр формула коши
- •49. Фкп в комп области степ ряд
- •50. Ряд тейлора в фкп
- •51. Ряд лорана фкп
- •52. Особые точки
- •53. Вычеты
- •54. Основн теор вычет
- •55. Вычисл вычет интегр
- •57. Теор подобия смещен опереж
- •58. Ди и инт изобр
- •59. Свертка
53. Вычеты
Если ф-ция
аналитическая в какой-то конкр.
окрестности z=a,
она может быть разложена в ряд Лорана:
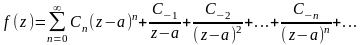 Особую
роль среди коэф-тов играет коэф-т С-1.
Он наз. вычетом ф-ции f(z)
в точке z=a.
Особую
роль среди коэф-тов играет коэф-т С-1.
Он наз. вычетом ф-ции f(z)
в точке z=a.

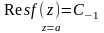 .
.
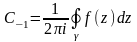 ,
где контур
замкнутый контур, окружающий точку
z=a
и положительно ориентированный. В
качестве
можно взят окр. С центром в точке а
достаточно малого радиуса (чтобы контур
не содержал внутри других особых точек).
,
где контур
замкнутый контур, окружающий точку
z=a
и положительно ориентированный. В
качестве
можно взят окр. С центром в точке а
достаточно малого радиуса (чтобы контур
не содержал внутри других особых точек).
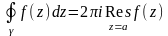 .
.
Вычисление вычетов в полюсе.
Пуст точка z=a
явл. полюсом 1-ого порядка. В этом случае
разложение в ряд Лорана
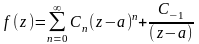 .
Домножим f(z)
на z-a
.
Домножим f(z)
на z-a
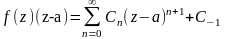 .
Переходя к пределу при
.
Переходя к пределу при
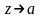 ,
получим, что
,
получим, что
 .
.
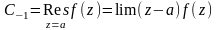

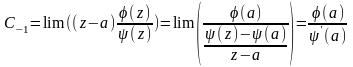
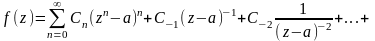
 .
Умножим выражение на (z-a)k
.
Умножим выражение на (z-a)k
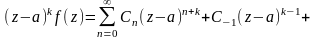
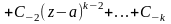 .
Продифференцировать к-1 раз это выражение
и переходя к пределу при
,
получим:
.
Продифференцировать к-1 раз это выражение
и переходя к пределу при
,
получим:
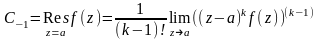 .
.
54. Основн теор вычет
Пусть ф-ция f(z) аналитична в некоторой области за исключением крнечного числа особых точек, то согласно теореме (интегр.) Коши для многосвязной области:
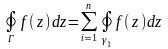 .
С другой стороны, если интеграл расписать
как
.
С другой стороны, если интеграл расписать
как
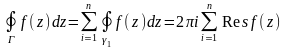
55. Вычисл вычет интегр
Если R(sinx,cosx)
– рациональная функция от sinx,cosx,
непрерывная при
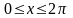 (или
(или
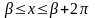 ),
то, сделав подстановку
),
то, сделав подстановку
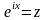 ,
можно показать, что
,
можно показать, что
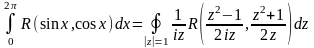
Значение интеграла в правой части этого выражения равно сумме вычетов подынтегральной функции относительно полюсов, лежащих внутри окружности |z|=1, умноженной на 2πi.
2.
Если f(z)
– дробно-рациональная функция,
аналитическая на действительной оси
и в верхней полуплоскости(Imz>0),
за исключением конечного числа особых
точек z1…zn,
лежащих в верхней полуплоскости (т.е.
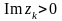 ),
и если
),
и если
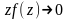 при
при
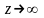 ,
то
,
то
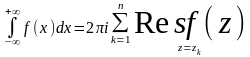 .
.
3.Если
f(z)
-- дробно-рациональная функция,
аналитическая на действительной оси
и в верхней полуплоскости, за исключением
конечного числа особых точек z1…zn,
лежащих в верхней полуплоскости , и
если
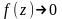 при
,
то для любого
при
,
то для любого
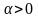
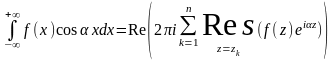 ;
;
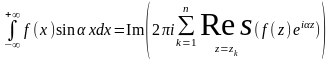 .
.
56. Св-ва оригиналов и изобр
Оригинал
- ф-ция f(t)
удовлетворяющая условиям: 1)f(t)=0
при t<0;
2)сущ. M>0и
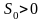 такие, что |f(t)|<=
такие, что |f(t)|<=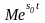 ,где
,где
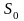 -показатель
роста f(t);
3)f(t)-непрерывная
или кусочно-непрерывная.
-показатель
роста f(t);
3)f(t)-непрерывная
или кусочно-непрерывная.
Изображение-
ф-ция
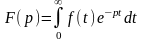 ,
где
,
где
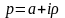 (компл.
число). При t>0
интеграл сходится к полуплоскости, где
(компл.
число). При t>0
интеграл сходится к полуплоскости, где
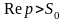 .
.
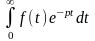 =L[f(t)]
Если f(t)-оригинал,F(p)-изображение
=L[f(t)]
Если f(t)-оригинал,F(p)-изображение
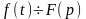 или
или
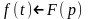
Свойства изображения:
-линейность
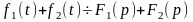
c-const

57. Теор подобия смещен опереж
Если
f(t)-оригинал,
а его изображение F(p)
,
то для любого α
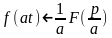 .
.
Док-во:
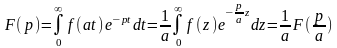 αt=z
αt=z

 ч.т.д
ч.т.д
теор смещения
Если
f(t)-оригинал,
а его изображение F(p)
,
то для любого
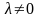
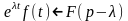 .
.
Док-во:
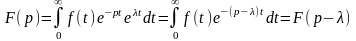 ч.т.д
ч.т.д
2)Метод Даламбера для решения уравнений в частных производных.
U(x,0)=φ(x);
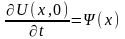
U(0,t)=0; U(l,t)=0
Пусть
решение имеет вид
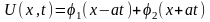 .
Оно удовлетворяет краевым условиям.
.
Оно удовлетворяет краевым условиям.
теор запазд
Если
f(t)-оригинал,
и
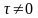 то
то
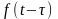 ←
←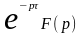
Доказательство:
F(p)=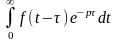
=│t-τ=z t=z+τ dt=dz│=
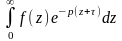 =
=
=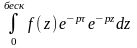 =
=
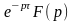 ,
ч.т.д.
,
ч.т.д.
58. Ди и инт изобр
Т.
Если
и
предел
 и
и
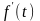 –
ориг., то изображ. оригинала
–
ориг., то изображ. оригинала
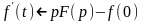 .
.
Док-во:
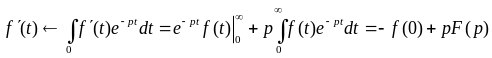
Если
f(t)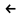 F(p),
то
F(p),
то
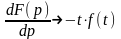
Док-во:
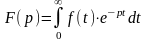 (по определению).
Продифференцируем обе части:
(по определению).
Продифференцируем обе части: