- •1. Числ ряды
- •2.Действия над рядами Св-ва
- •3. Необх признак сх
- •6. Ряды с неотр Признаки сравнения
- •7. Признак Даламбера.
- •3) В случае ответа о сходимости или расходимости ряда теорема не дает.
- •9. Интегральный признак Коши.
- •10.Знакпер ряд абс и услвн сх
- •12. Знакчеред ряды Лейбниц
- •14. Функ ряды область сх
- •15. Равн сх фр Вейерштрассе
- •17. Степ ряд Абель
- •25. Решение ду
- •27 Тригон ряд фурье
- •32. Разлож непериод функ
- •33. Тригоно ряд фурье в комп форме
- •34. Интеграл фурье
- •35 Комп форма инт фурье
- •36. Опред фкп
- •37. Предел и непрерывн фкп
- •42. Общая степен
- •43. Условие коши-риманна
- •47. Основн теор коши
- •48. Интегр формула коши
- •49. Фкп в комп области степ ряд
- •50. Ряд тейлора в фкп
- •51. Ряд лорана фкп
- •52. Особые точки
- •53. Вычеты
- •54. Основн теор вычет
- •55. Вычисл вычет интегр
- •57. Теор подобия смещен опереж
- •58. Ди и инт изобр
- •59. Свертка
10.Знакпер ряд абс и услвн сх
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно сходящимся.
11. св-ва абс сх рядов
1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (теорема Дирихле).
2. Абсолютно
сходящиеся ряды с суммами
 и
и
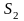 можно почленно складывать (вычитать).
можно почленно складывать (вычитать).
3. Под произведением
двух рядов
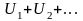 и
и
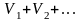 понимают
ряд вида
понимают
ряд вида
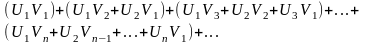 Произведение
двух абсолютно сходящихся рядов с
суммами
и
есть абсолютно сходящийся ряд, сумма
которого равна
Произведение
двух абсолютно сходящихся рядов с
суммами
и
есть абсолютно сходящийся ряд, сумма
которого равна
12. Знакчеред ряды Лейбниц
Если в знакочередующемся
ряду
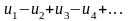 ,
где
,
где
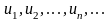 положительны,
члены таковы, что
положительны,
члены таковы, что
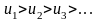 и
и
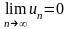 ,
то ряд сходится, его сумма положительна
и не превосходит первого члена.
,
то ряд сходится, его сумма положительна
и не превосходит первого члена.
Доказательство:
Рассмотрим сумму
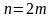 первых членов ряда.
первых членов ряда.
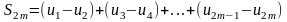 >0,
т.к. все скобки положительны. Запишем
теперь эту же сумму так:
>0,
т.к. все скобки положительны. Запишем
теперь эту же сумму так:
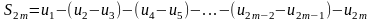 По
условию 1 каждая из скобок положительна.
Поэтому в результате вычитания этих
скобок из
По
условию 1 каждая из скобок положительна.
Поэтому в результате вычитания этих
скобок из
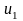 мы получим число, меньшее
.
Таким образом, мы установили, что
мы получим число, меньшее
.
Таким образом, мы установили, что
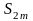 при
возрастании m
возрастает и ограничена сверху. Отсюда
следует, что
имеет
предел S
при
возрастании m
возрастает и ограничена сверху. Отсюда
следует, что
имеет
предел S
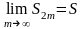 ,
причем
,
причем
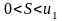 .
Однако сходимость еще не доказана. Мы
доказали только, что последовательность
четных частичных сумм имеет пределом
число S.
Докажем теперь, что нечетные частичные
суммы также стремятся к пределу S.
Рассмотрим для этого сумму
.
Однако сходимость еще не доказана. Мы
доказали только, что последовательность
четных частичных сумм имеет пределом
число S.
Докажем теперь, что нечетные частичные
суммы также стремятся к пределу S.
Рассмотрим для этого сумму
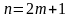 первых членов исходного ряда.
первых членов исходного ряда.
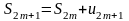 .
Так как по условию 2 теоремы
.
Так как по условию 2 теоремы
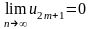 ,
то следовательно
,
то следовательно
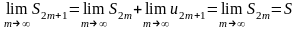 Тем
самым мы доказали, что
как при четном n,
так и при нечетном. Следовательно,
исходный ряд сходится
Тем
самым мы доказали, что
как при четном n,
так и при нечетном. Следовательно,
исходный ряд сходится
14. Функ ряды область сх
Функ. ряд – ряд,члены которого являются функ. одного и того же аргумента.
Ф.р.: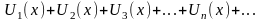
Совокупность значений x, при которых ф.ряд сходится - область сходимости ф.ряда.
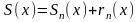 ;
;
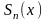 -
n-частичная
сумма ,
-
n-частичная
сумма ,
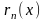 -
остаточный член
-
остаточный член

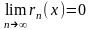 =lim
=lim
Если ряд сходится, то
15. Равн сх фр Вейерштрассе
П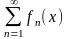 усть
дан функциональный ряд
усть
дан функциональный ряд
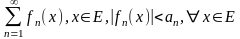 и если
и если
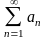 – сходится, то функциональный ряд
сходится равномерно на E.
– сходится, то функциональный ряд
сходится равномерно на E.
Д оказательство:
Т.к. ряд сходится, то по критерию Коши: для
любого
ε>0 существует такой номер N, что
 ε для всех n>N и любых целых p>=0.
Поэтому для всех n>N и
ε для всех n>N и любых целых p>=0.
Поэтому для всех n>N и
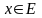
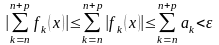 .
Это означает, что ряд
.
Это означает, что ряд
сходится равномерно на множестве Е
16. Св-ва равн сх почлен диф и инт
Если ряд состоящий из непрерывных функций, сходится равномерно на [а, b] к сумме S(x), то интеграл от суммы этого ряда = сумме интегралов от его членов.
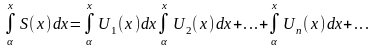 , где α и х є [a,
b]
, где α и х є [a,
b]
Дифференцирование функциональных рядов.
Теорема
Если функциональный ряд (1)
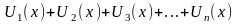 сходится к сумме S(x)
на [a, b], и ряд (2)
сходится к сумме S(x)
на [a, b], и ряд (2)
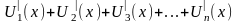 ,
составленный из производных членов
данного ряда равномерно сходится на
[a,
b]
к сумме σ(x),
то сумма ряда, составленного из
производных, равна производной от суммы
ряда (1), т.е. σ(x)=
,
составленный из производных членов
данного ряда равномерно сходится на
[a,
b]
к сумме σ(x),
то сумма ряда, составленного из
производных, равна производной от суммы
ряда (1), т.е. σ(x)=