1. Числ ряды

Числ ряд – сумма упорядоченного мн-ва чисел;

a₁+а₂+а₃+…+а_n+…

a_i- член числ послед-ти

Частичные суммы ряда:

S₁=a₁

S₂=a₁+a₂

S₃=a₁+a₂+a₃

S_n=a₁+a₂+a₃+…+a_n

Сумма ряда – предел вида S=lim_n→∞S_n, если он сущ.

Если предел не существует или =∞ — ряд расход, в противн случае сходиться

S=S_n+r_n

r_n– остаток ряда(остаточный член)

Если ряд сходиться, то r_n →0 при n→∞

2.Действия над рядами Св-ва

Св-ва:

1) если ряд (1) сходиться в сумме S, то и ряд, полученный из данного при умножении a_i на λ (i=1,n), тоже сходиться, и его сумма равна λS.

Док-во: lim_n→∞S_n=S

S_n= a₁+a₂+a₃+…+a_n

δ_n= λa₁+ λa₂+ λa₃+…+ λa_n

lim_n→∞δ_n= λ lim_n→∞S_n= λS

2) Если сходиться ряд (1) в сумме S, и сходиться ряд (2) b₁+b₂+b₃+…+b_n в сумме δ, то и сходиться ряд 3 (a₁±b₁ +a₂±b₂ +a₃±b₃ +…+a_n±b_n+…) в сумме S±δ

Док-во: аналогично.

3. Необх признак сх

(1) a₁+а₂+а₃+…+а_n+…

Если числовой ряд (1) сходиться, то предел его n-го члена при n→∞ равен 0

Док-во: по определению ряд сходится =>

Сущ. lim_n→∞S_n=S

Если последовательность имеет предел, то он единственный

lim_n→∞S_n+1=S

lim_n→∞(S_n+1-S_n)=S-S=0

lim_n→∞a_n+1=0, ч.т.д.

6. Ряды с неотр Признаки сравнения

Пусть имеем два ряда с положительными членами

a₁+a₂+…+a_n+…(1) и b₁+b₂+…+b_n+… (2), для которых выполняется условие: a_n b_n. Тогда 1) если сходится ряд (1), то сходится и ряд (2); 2) если ряд (2) расходится, то расходится и ряд (1) .

Док-во:

Поскольку и a_n, b_n — положительные, то м. утверждать: , где S_n и σ_n — n-частичные суммы 1-го и 2-го рядов;

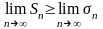
значит, если существует 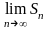(ряд 1 сходится), то существует и 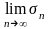(ряд 2 сходится)

7. Признак Даламбера.

Если в ряду с положительными членами 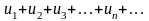отношение (n + 1)-го члена к n-му при 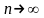имеет конечный предел l, то есть 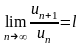, то

ряд сходится в случае ;

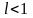ряд расходится в случае ;

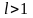3) в случае 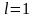ответа о сходимости или расходимости ряда теорема не дает.

8. Радикальный признак Коши.

Если для ряда с положительными членами величина 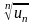имеет конечный предел l при , то есть , то

в случае ряд сходится;

в случае ряд расходится;

3) В случае ответа о сходимости или расходимости ряда теорема не дает.

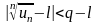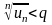Пусть . Рассмотрим число q, удовлетворяющее соотношению . Начиная с некоторого номера n=N будет иметь место соотношение . Отсюда следует, что или 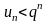для всех 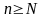. Рассмотрим теперь два ряда: (1) и 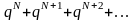(2). Ряд 2 сходится, так как его члены образуют убывающую геометрическую прогрессию. Члены ряда 1, начиная с 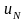, меньше членов ряда 2. Следовательно, ряд 1 сходится.

Пусть . Тогда, начиная с некоторого номера n=N будем иметь или . Но если все члены рассматриваемого ряда, начиная с , больше 1, то ряд расходится, так как его общий член не стремится к нулю.

9. Интегральный признак Коши.

Пусть члены ряда положительны и не возрастают, то есть 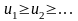и пусть f(х) – такая непрерывная не возрастающая функция, что , , .

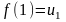Тогда справедливы следующие утверждения: если несобственный интеграл 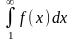сходится, то сходится и исходный ряд;

если указанный интеграл расходится, то расходится и исходный ряд.

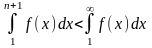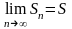Предположим, что интеграл сходится, то есть имеет конечное значение. Так как , то , то есть частичная сумма Sn остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены u_n положительны. Следовательно, Sn при имеет конечный придел , то есть ряд сходится.