13. Критерий оптимальности для максимизации задач.

1. –Δj>0; z2-z1>0 – произошло улучшение целевой ф-ии

2. –Δj<0, z2-z1<0 , -Δj=0 z2-z1=0 – улучшения не происходит.

Теорема 1. Критерии оптимальности значения целевой функции в задаче на максимум. Опорный план x* является опт-м, если все Δj>=0, i=1,n.

Теорема 2. Если Δk<0, j=k для некоторого столбика j=k, и среди значений aik нет положительных, то целевая ф-ия будет неограниченной.

Теорема 3. Если опорный план x* не вырожден и Δk<0 для j=k, среди чисел aik есть положительные числа, то сущ-т опорный план x1, в котором значение целевой ф-ии будет больше, чем в точке x*: z(x1)>z(x*).

Метод искусственного базиса. М-метод.

Если в системе ограничений нет исходного опорного решения, то в ограничения вида “>=” и “=” добавляют искусственные переменные yi>=0 для получения исходного опорного решения. ai1x1+ai2x2+…+ainxn>=bi ; ai1x1+ai2x2+…+ainxn – xm+I +yi=bi

F=C1x1 +…+Cnxn – M(Σ _i=1 ^m yi).

При решении задачи на макс, в целевую ф-ию добавляется слагаемое вида – M(Σ _i=1 ^m yi), где М – достаточно большое число: М>>oo. В задачах на min добавляем слагаемое вида – +M(Σ _i=1 ^m yi). Теорема. Пусть задана М-задача. Если в опт-решении x*(x1,x2…xn,y1…ym) все искусственные переменные yi=0, то план исходной задачи x(x1,x2…xn) явл-ся оптимальным. Теорема. Если в опт-решении М-задачи хотя бы одна искусственная переменная отлична от нуля, то исходная задача не имеет допустимых планов.

14. Двойственные задачи. Экономическая интерпретация двойственных задач.

Каждой задаче линейного программирования можно сопоставить некоторую другую ЗЛП, называемую двойственной или сопряженной по отношению к исходной или прямой задаче.

{a11x1+a12x2+…+a1nxn<=b1 |y1

{a21x1+a22x2+…+a2nxn<=b2 |y2

{….. | (1)

{am1x1+am2x2+…+amnxn<=bm |ym

xi>=0, i=1,n (2)

F=C1x1+C2x2+…+Cnxn  max (3)

{a11y1+ a21y2+…+am1ym≥C1

{a12y1+a22y2+…+am2ym≥C2 (4)

{……..

{a1ny1+a2ny2+…+amnym≥Cn

yj≥0, j=1,m (5)

f=b1y1+b2y2+…+bmym min (6)

Пара задач (1)-(3) и (4)-(6) наз-ся парой симметричных двойственных задач.

Векторно-матричная запись:

{AX<=B

{X≥0

F=CX max

{A^TY≥C^T

{Y≥0

F=B^TYmin – симметричная ДЗ.

Несимметричные ДЗ

1. {ai1x1+ai2x2+…+ainxn=bi;

2. {ai1x1+ai2x2+…+ainxn>=bi

{ai1x1+ai2x2+…+ainxn<=bi;

3. { ai1x1+ai2x2+…+ainxn<=bi

{ ai1x1+ai2x2+…+ainxn<=bi;

Алгоритм решения НДЗ:

1. Если на переменную xj в ПЗ накладывается усл-ие неотрицательности, то соотв. Ограничение ДЗ записывается в виде нер-ва и наоборот.

2. Если на переменную xj ПЗ не наклад-ся усл-я неотр-ти, то соотв-ие усл-я ДЗ записываются в виде рав-ва, и наоборот.

Экономический смысл

Пусть через X_j обозначен объем производства j - го вида продукта, через B_j - запас i - го вида сырья, через A_ij - затраты i - го сырья на производство единицы j - го продукта и через C_j - стоимость единицы j - го продукта.

Возникает задача максимизации

при условиях

X_j і 0 ( j = 1 .. n ).

Если интерпретировать Y_i как объективную оценку стоимости единицы i-го сырья, то стоимость ресурсов, затраченных на производство единицы j - го продукта, должна быть не меньше объявленной стоимости и общая стоимость затраченного сырья должна быть минимальной.

Отсюда появляется задача минимизации при заданных условиях, т.е. возникает пара двойственных задач:

Здесь первая теорема двойственности утверждает равенство стоимости затраченных ресурсов и объявленной стоимости произведенной продукции. Что касается теоремы 2, то если при некотором i выполняется неравенство

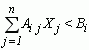
то i-е сырье не является лимитирующим и объективная его стоимость Y_i=0.

Таким образом, в рассмотренной постановке двойственная задача является математической формулировкой объективной оценки всех производственных факторов.