5. Теорема о выпуклом многоугольнике.
М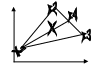
нож-во
– замкнутое, если оно содержит все свои
граничные точки. Множ-ва наз-ся
ограниченным, если сущ-т такой шар,
который полностью в себе содержит
заданное множ-во. Выпуклое ограниченное
множ-во точек плоскости (пространства),
имеющее конечное число угловых точек,
наз-ся многоугольником (многогранником).
Если же множ-во не ограничено, наз-ся
выпуклой многоугольной (многогранной)
областью.
Теорема. Выпуклый n-мерный многоугольник явл-ся выпуклой линейной комбинацией своих угловых точек. Док-во: Пусть n=2, а в кач-ве многоуг-ка рассмотрим треуг-к. x€ Δx1x2x3, x=a1x1+a2x2+a3x3; a1+a2+a3=1, ai>=0,
X=β1x1+β4x4; β1+β4=1,X4=β2x2+β3x3, β2+β3=1; x=b1x1+b2b4x2+b3b4x3, b1+b2b4+b3b4=1, b1+b4(b2+b3)=1, b2+b3=1.
6. Теорема: множество решений ЗЛП является выпуклым. Док-во:
{AX≤B
|Z=C*Xmax
{X≥0
ЗЛП имеет два решения:
X1(x11,x12…x1n), X2(x21,x22…x2n). Ax1=B, x1>=0; Ax2=B, x2>=0.
Рассмотрим некоторый произвольный вектор Х, кот явл выпуклой линейной комбинацией решений Х1 и Х2:
X=a1X1+a2X2; a1+a2=1; a1>=0, a2>=0. Докажем, что данный вектор также явл-ся решением ЗЛП:
A(a1x1+a2x2)=a1AX1+a2AX2=a1B+a2B=(a1+a2)B=B.
7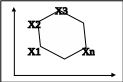
.
Теорема об экстремальном значении
целевой функции. Если ЗЛП имеет
оптимальное решение, то целевая ф-ия
принимает его в одной из угловых точек
многоугольника решений. Если целевая
ф-ия принимает опт. Решение более чем в
одной угловой точке, то она принимает
его и в любой точке, являющейся выпуклой
линейной комбинацией указанных угловых
точек.
Док-во:
Пусть Х* явл-ся опт-решением. Тогда значение целевой ф-ии в этой точке F(X*)>=F(Xi), i=1,n. Если Х* явл-ся одной из угловых точек, то теорема доказана. Предположим, что X* - внутренняя точка. Тогда
X*=E i=1 n aiXi, E i=1 n =1, ai>=0. Найдем значение целевой ф-ии в точке Х*:
F(X*)=F(E i=1 n aiXi) = <в силу линейности F, F в сумме равна сумме ф-ий>
= E i=1 n aiF(Xi) (1), max F(xi) =M. Тогда вместо каждого слагаемого ставим M:
(1)≤F(X*)≤M, => F(X*)=M, чтд.
Предположим, что опт-значение целевая ф-ия принимает в точках x1,x2…xq.
Тогда опт-решение можно представить в виде суммы:
q<n
X*= E i=1 q aiXi E i=1 q ai=1, F(X*)=F(E i=1 q aiXi)= E i=1 q ai F(Xi)=
= E i=1 q aiM=M E i=1 q ai=M. В данном случае, решений – бесконечное множ-во.
8. Опорные прямые. Опорные решения. Симплексные преобразования.
Опорной прямой к множеству М в его точке А называется прямая, проходящая через точку А так, что множество М целиком лежит с одной стороны от этой прямой, т. е. в одной из определяемых прямой замкнутых полуплоскостей.
Допустимое базисное решение называется опорным решением.
Метод однократного замещения. Пусть система приведена к единичному базису. Если все свободные члены системы оказались неотрицательными, то полученное базисное решение – опорное. Для перехода к след. опорному решению используют правило:
1.Разрешающим выбирают неединичный столбец, в котором есть хотя бы один неотриц элемент. 2. Составляют отношение свободных членов только к положит. коэф-там разрешающего столбца. 3. Разрешающим выбирается то ур-ие, для кот. указанное отношение явл-ся минимальным. При этом необходимо следить, чтобы решения не повторялись. Указанные преобразования называют симплексными преобразованиями.