35. Решение матричной игры в смешанных стратегиях.

Совокупность (комбинация) чистых стратегий A₁, A₂, …A_m и B_1, B_2, …B_n в сочетании с векторами вероятностей выбора каждой из них называются смешанными стратегиями.

Теорема фон Неймана: каждая конечная матричная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

В таких играх решением будет пара оптимальных смешанных стратегий P^* и Q^*, таких, что если один из игроков придерживается своей оптимальной стратегии, то и другому игроку не выгодно отклоняться от своей оптимальной стратегии.

Средний выигрыш игрока A определяется математическим ожиданием:

M_A(P, Q) p_i q_j .

Если вероятность (относительная частота) применения стратегии отлична от нуля, то такая стратегия называется активной.

Стратегии P^*, Q^* называются оптимальными смешанными стратегиями, если

M_A(P, Q^*) ≤ M_A(P^*, Q^*) ≤ M_A(P^*, Q) (1)

В этом случае M_A(P^*, Q^*) называется ценой игры и обозначается через V (V_* ≤ V ≤ V^*). Первое из неравенств (1)означает, что отклонение игрока A от своей оптимальной смешанной стратегии при условии, что игрок B придерживается своей оптимальной смешанной стратегии, приводит к уменьшению среднего выигрыша игрока A. Второе из неравенств означает, что отклонение игрока B от своей оптимальной смешанной стратегии при условии, что игрок A придерживается своей оптимальной смешанной стратегии, приводит к увеличению среднего проигрыша игрока B.

V_* ≠V* - решения в чистых стратегиях не существует. Припишем строкам платёжной матрицы неизвестные вероятности p₁ и p₂ (вероятности выбора стратегий A₁ и A₂) соответственно, получим линейную зависимость – математическое ожидание (средний выигрыш) игрока A при применении игроком B второй стратегии. Поскольку мы разыскиваем оптимальное решение первого игрока A , которое не должно зависеть от выбора стратегий вторым игроком B, приравняем полученные зависимости средних выигрышей. получаем оптимальную смешанную стратегию игрока A. Аналогично с В (вероятности qn).

36. Приведение матричной игры к злп.

Алгоритм поиска решения матричной антагонистической игры, заданной платежной матрицей, имеющей размерность m×n при больших значениях m и n, сводится к алгоритму симплекс-метода решения пары взаимодвойственных задач линейного программирования. Покажем, как привести конечную матричную антагонистическую игру к двум взаимодвойственных задачам линейного программирования.

Пусть антагонистическая игра задана платёжной матрицей A, имеющей размерность m×n, и эта игра является не вполне определённой. Необходимо найти решение игры, т.е. определить оптимальные смешанные стратегии первого и второго игроков:

P^*= (p₁^*, p₂^*, …, p_m^*), Q^*= (q₁^*, q₂^*,…, q_n^*)

где P^* и Q^* – векторы, компоненты которых p_i^* и p_j^* характеризуют вероятности применения чистых стратегий i и j соответственно первым и вторым игроками и соответственно для них выполняются соотношения:

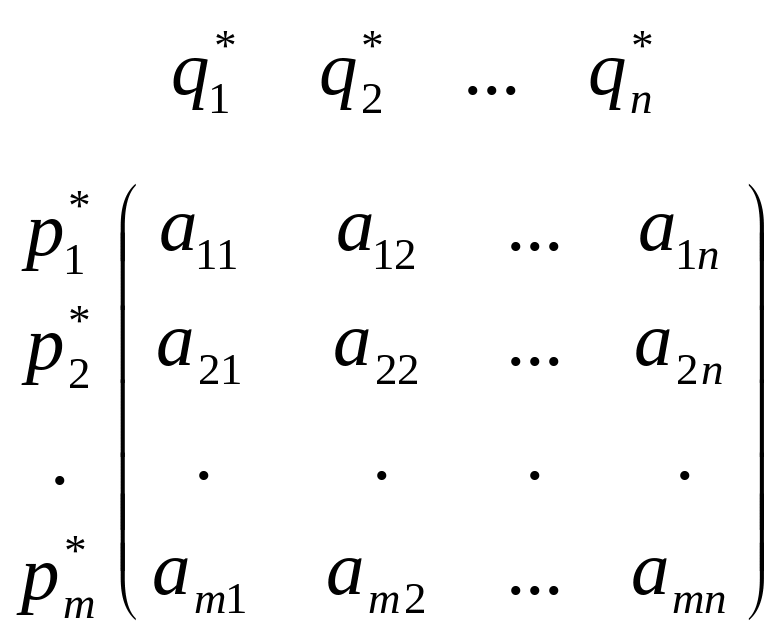
Общий алгоритм нахождения решения конечной антагонистической игры произвольной размерности m×n.

1. На основании анализа платёжной матрицы следует определить, существуют ли в ней доминируемые стратегии, и исключить их.

2. Найти верхнюю и нижнюю цены игры и определить, имеет ли данная игра седловую точку (нижняя цена игры должна быть равна верхней цене игры).

3. Если седловая точка существует, то оптимальными стратегиями игроков, являющимися решением игры, будут их чистые стратегии, соответствующие седловой точке. Цена игры равна верхней и нижней цены игры, которые равны между собой.

Если игра не имеет седловой точки, то решение игры следует искать в смешанных стратегиях. Для определения оптимальных смешанных стратегий в играх m × n следует использовать симплекс-метод, предварительно переформулировав игровую задачу в задачу линейного программирования.