Специальные виды векторных полей. Соленоидальое

О. Векторное поле a, для всех точек которого дивергенция равна нулю, называется соленоидальным. Свойства соленоидального поля: 1. В соленоидальном поле a поток вектора, через любую замкнутую поверхность равен нулю, т.е. соленоидальное поле не имеет источников и стоков. Док-во. Это свойство следует из формулы Г-О:

K= = =0, т.к. div a = 0 (ч.т.д.). 2. Каждое соленоидальное поле является полем ротора некоторого векторного поля, т.е. если div a = 0, то существует такое векторное поле b, что a = rot b, вектор b называюь вектором-потенциалом данного поля. 3.В соленоидальном поле поток вектора в направлении векторных линий через каждое сечение векторной трубки один и тот же. Это следует из того, что в поле скоростей текущей жидкости количество жидкости, втекающей за единицу времени в часть векторной трубки равно количеству жидкости, вытекающей из неё.

Специальные виды векторных полей. Потенциальное

О. Векторное поле a, для всех точек которого ротор равен нулю, называется потенциальным rot a = 0. Свойства потенциального поля. Циркуляция потенциального поля a по любому замкнутому контуру равна нулю. Док-во. Это св-во следует из ф-лы Стокса: С= = =0, т.к. rot a = 0 (ч.т.д.) 2. Вектор a потенциального поля является градиентом некоторой скалярной функции. Справедливо и обратное утверждение: поле градиента скалярной функции u=u(x,y,z) является потенциальным.

3. Если поле а потенциальное, то потенциал поля u(x,y,z) в произвольной точке P(x,y,z) мажет быть вычилсен по формуле: u(P)=u(x,y,z)= , где А – фиксированная точка. Для вычисления интеграла, для простоты выбирают путь со звеньями, параллельными осями координат, соединяющий точки А и Р. За точку а можно взять нач. коорд. u(x,y,z)= a_xdx+a_ydy+a_zdz+C= a_x(x,0,0)dx+ a_y(x,y,0)dx+ a_z(x,y,z)dx+С.

Специальные виды векторных полей. Лапласово (гармоническое)

О. Векторгое пол называется лапласовым, если оно одновремнно является соленоидальным и потециальным. Пример гармонического поля: поле тяготения. Поскольку поле потенциальное, то a = grad u, причем rot a = 0, u – потенциал поля. Условие соленоидальности означает, что div a = 0.

div a = div grad u = ▼∙(▼u) = ∆u = 0. ∆u= Вывод: в гармоническом поле лапласиан равен нулю. О. Функции, лапласиан которых равен нулю называют гармоническими.

Теорема о разложении векторных полей.

Т. Всякое векторное поле можно представить в виде суммы соленоидального и потенциального векторных полей a=a_n+a_c. Из определений соленоидального и потенциального векторных полей следует, что a_n=grad u, div a_c=0. Из теоремы a-a_n=a_c, тогда div (a-a_n) = div a_c = 0 => div a – div a_n = 0 => div a – div grad u = 0 => div a - ∆u = 0. Итак, для решения задачи разложения требуются три равенства: 1). a_n = grad u; 2). a_c = a – a_n; 3). div a = ∆u.

Применение вычетов к вычислению контурных интегралов

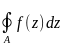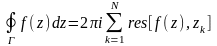Для вычисления контурных интегралов используются первая и вторая теоремы о вычетах: 1. Интеграл равен произведению (2πi) на сумму вычетов относительно особых точек f(z), лежащих внутри контура Г: . 2. Сумма всех вычетов относительно особых точек f(z) равна нулю: .
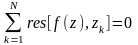