
- •Понятия фкп. Выражения для х и у.
- •Основные Элементарные функции
- •Предел и непрерывность фкп
- •Дифференцируемость. Условие Коши-Римана
- •Гармонические функции. Гармонические пары.
- •Определение и св-ва аналитических функций
- •Конформность отображения посредством гармонической пары и аналитической функции. Геометрический смысл модуля и аргумента производной.
- •Линейная функция
- •Простейшая дробно-линейная функция
- •Степенная функция
- •Дробно-линейная функция
- •Интегрирование по комплексному аргументу
- •Теорема Коши. Интегральная формула Коши
- •Ряды с комплексными членами
- •Изолированные особые точки и их классификация
- •Ряд Тейлора
- •Ряд Лорана
- •Основные теоремы о вычетах
- •Скалярное поле. Определение. Линии и поверхности уровня.
- •Скалярное поле. Производная по направлению.
- •Скалярное поле. Градиент
- •Векторное поле. О. Векторные линии и векторные трубки
- •Поток векторного поля. О. Вычисление.
- •Дивергенция векторного поля. О. Выч. Теорема г-о
- •Циркуляция векторного поля. О. Вычисление
- •Ротор векторного поля. О. Выч. Теорема Стокса
- •Оператор Гамильтона. Диф-ые операции II порядка
- •Специальные виды векторных полей. Соленоидальое
- •Специальные виды векторных полей. Потенциальное
- •Специальные виды векторных полей. Лапласово (гармоническое)
- •Теорема о разложении векторных полей.
- •Применение вычетов к вычислению контурных интегралов
- •Применение тфкп
- •Определение функционального анализа. Предмет функционального анализа.
- •Определение евклидова пространства
- •Определение линейных пространств. Аксиомы. Свойства
- •Линейные операторы. Действия с лин. Операторами
- •Базис и матрица линейного оператора Собственные значения и собственные векторы линейного оператора
- •Квадратичные формы. Матрица квадратичной формы. Пример.
- •Ортогональный и ортонормированный базис
- •Понятие меры. Измеримые функции. Простые функции. Ортогональные функции
- •Мера Лебега. Свойства меры Лебега. Интеграл Лебега
- •Нормированные пространства. Норма. Примеры
- •Метрические пространства. Метрика. Примеры. Сжатые отображения
- •Ортогональный и ортонормированный базис. Процесс Ортогонализации. Сопряженные векторы в евклидовом пространстве.
- •Дифференциальные уравнения с частными производными
- •Основные уравнения математической физики
- •Явная и Неявная разностная схема
Дифференцируемость. Условие Коши-Римана
О. Функция ω = f(z) = u (x,y) + iv(x,y) называется дифференцируемой в точке z, если ее приращение можно записать в виде ∆ω = ∆f(z) = A∆x - B∆y + i(A∆y+B∆x) +α∆x - β∆y +
+ (α∆y + β∆x), где А и В не зависят от ∆x и ∆y, а α→0, β→0 при ∆x→0, ∆y→0.
Т. Для того чтобы функция ω = f (z) была дифференцируемой в точке z необходимо и достаточно, чтобы она имела в этой точке конечную производную f ’(z) = A+ iB.
О. Если ω = f (z) имеет производную в точке z, то она называется дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке некоторой области D плоскости Гаусса, называется дифференцируемой в области D.
Т. Дифференцируемая функция ω = f (z) в точке z (или в области D) непрерывна в этой точке (или области).
Теорема.
Для того
чтобы функция f(z)
= u(x,y)
+ i
v(x,y),
определенная в некоторой области D,
была дифференцируемой в точке z
этой области
необходимо и достаточно, чтобы в этой
области существовали непрерывные
частные производные функций u(x,y)
и v(x,y),
и выполнялись условия
 ,
,
 ,
называемые условиями
Коши - Римана
или Эйлера – Даламбера, кратко, условиями
КРЭДа.
,
называемые условиями
Коши - Римана
или Эйлера – Даламбера, кратко, условиями
КРЭДа.
Следствие.
Так как
производная
дифференцируемой функции комплексного
переменного равна f
’(z)
= A+
iB
(по теореме
2), где A=
,B=
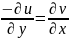 ,
то она может быть найдена по одной из
формул:
,
то она может быть найдена по одной из
формул:
f
’(z) =
 ,
f ’(z) =
,
f ’(z) =
 ,
f ’(z) =
,
f ’(z) =
 ,
f ’(z) =
,
f ’(z) =
 .
.
Гармонические функции. Гармонические пары.
О.
Функция u
= u(x,y)
называется гармонической,
если ее лапласиан равен нулю:

 .
О. Две
сопряженные
гармонические функции u(x,y)
и v(x,y)
называются гармонической
парой.
.
О. Две
сопряженные
гармонические функции u(x,y)
и v(x,y)
называются гармонической
парой.
О.
Гармонические в
области D
функции u(x,y)
и v(x,y)
называются сопряженными гармоническими
в области
 ,
если для их частных производных в
области D1
выполняются условия КРЭДа
,
если для их частных производных в
области D1
выполняются условия КРЭДа
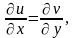

Определение и св-ва аналитических функций
О. (первое определение аналитической функции) Функция ω = f(z), дифференцируемая в каждой точке z области D и имеющая в этой области непрерывную производную f '(z), называется аналитической в области D.
Некоторые свойства аналитических функций.
1. Функция, аналитическая в точке, имеет в этой точке производные любого порядка, которые являются непрерывными в этой точке. Аналитическая в области D функция дифференцируема, а, следовательно, и непрерывна в этой области.
2. Сумма, разность, произведение и частное (если делитель не равен нулю) двух аналитических в области D функций – аналитическая функция в D.
3. Если ω = f(z) – аналитическая функция в замкнутой области D, ограниченной контуром L, то ее значения внутри области D однозначно определяются ее значениями на контуре L. Если две аналитические в области D функции имеют на контуре L одни и те же значения, то они тождественны во всей области D.
4. (Теорема Дзядыка
В.К.) Если ω = f(z)
= u(x,y)
+i
v(x,y)
– аналитическая в области D
функция, то площади поверхностей z
= u(x,y),
z
= v(x,y),
z
= |f(z)|
=
 ,
расположенных в трехмерном пространстве
(Oxyz)
над любой частью области D,
равны.
,
расположенных в трехмерном пространстве
(Oxyz)
над любой частью области D,
равны.
5. Максимум модуля аналитической в области D функции не может располагаться во внутренней точке области D.
6. Пусть ω = f(z)
– аналитическая в области D
функция с областью значений G
= и пусть обратная к ней функция
и пусть обратная к ней функция
 аналитична
в области G.
Тогда сложная функция φ(f(z))
– аналитична
в области G.
аналитична
в области G.
Тогда сложная функция φ(f(z))
– аналитична
в области G.
