
- •Понятия фкп. Выражения для х и у.
- •Основные Элементарные функции
- •Предел и непрерывность фкп
- •Дифференцируемость. Условие Коши-Римана
- •Гармонические функции. Гармонические пары.
- •Определение и св-ва аналитических функций
- •Конформность отображения посредством гармонической пары и аналитической функции. Геометрический смысл модуля и аргумента производной.
- •Линейная функция
- •Простейшая дробно-линейная функция
- •Степенная функция
- •Дробно-линейная функция
- •Интегрирование по комплексному аргументу
- •Теорема Коши. Интегральная формула Коши
- •Ряды с комплексными членами
- •Изолированные особые точки и их классификация
- •Ряд Тейлора
- •Ряд Лорана
- •Основные теоремы о вычетах
- •Скалярное поле. Определение. Линии и поверхности уровня.
- •Скалярное поле. Производная по направлению.
- •Скалярное поле. Градиент
- •Векторное поле. О. Векторные линии и векторные трубки
- •Поток векторного поля. О. Вычисление.
- •Дивергенция векторного поля. О. Выч. Теорема г-о
- •Циркуляция векторного поля. О. Вычисление
- •Ротор векторного поля. О. Выч. Теорема Стокса
- •Оператор Гамильтона. Диф-ые операции II порядка
- •Специальные виды векторных полей. Соленоидальое
- •Специальные виды векторных полей. Потенциальное
- •Специальные виды векторных полей. Лапласово (гармоническое)
- •Теорема о разложении векторных полей.
- •Применение вычетов к вычислению контурных интегралов
- •Применение тфкп
- •Определение функционального анализа. Предмет функционального анализа.
- •Определение евклидова пространства
- •Определение линейных пространств. Аксиомы. Свойства
- •Линейные операторы. Действия с лин. Операторами
- •Базис и матрица линейного оператора Собственные значения и собственные векторы линейного оператора
- •Квадратичные формы. Матрица квадратичной формы. Пример.
- •Ортогональный и ортонормированный базис
- •Понятие меры. Измеримые функции. Простые функции. Ортогональные функции
- •Мера Лебега. Свойства меры Лебега. Интеграл Лебега
- •Нормированные пространства. Норма. Примеры
- •Метрические пространства. Метрика. Примеры. Сжатые отображения
- •Ортогональный и ортонормированный базис. Процесс Ортогонализации. Сопряженные векторы в евклидовом пространстве.
- •Дифференциальные уравнения с частными производными
- •Основные уравнения математической физики
- •Явная и Неявная разностная схема
Конформность отображения посредством гармонической пары и аналитической функции. Геометрический смысл модуля и аргумента производной.
Пусть
в области D
на плоскости (z)
задана аналитическая функция
 т.е. u(x,y)
и v(x,y)
– гармоническая пара. Зададим определенное
значение
т.е. u(x,y)
и v(x,y)
– гармоническая пара. Зададим определенное
значение
 .
Этому значению соответствует определенное
значение
.
Этому значению соответствует определенное
значение
 Следовательно, каждой точке z
= (x,y)
на плоскости (Oxy)
соответствует определенная точка ω
= (u,v)
на плоскости (Оuv)
и наоборот, т.е. задается взаимно-однозначное
отображение области D
плоскости (z)
на область G
плоскости (ω) посредством аналитической
функции или, что тоже самое, посредством
гармонической пары.
Следовательно, каждой точке z
= (x,y)
на плоскости (Oxy)
соответствует определенная точка ω
= (u,v)
на плоскости (Оuv)
и наоборот, т.е. задается взаимно-однозначное
отображение области D
плоскости (z)
на область G
плоскости (ω) посредством аналитической
функции или, что тоже самое, посредством
гармонической пары.
Т. Отображение посредством аналитической функции конформно при условии, что якобиан I 0.
Геометрический
смысл аргумента производной:
 – аргумент производной функции
– аргумент производной функции
 в точке Z0
геометрически равен углу
в точке Z0
геометрически равен углу
 ,
на который нужно повернуть касательную
L
в точке Z0
к кривой Г,
чтобы получить касательную
,
на который нужно повернуть касательную
L
в точке Z0
к кривой Г,
чтобы получить касательную
 в
точке ω0
к образу
этой кривой Г/.
Геометрический
смысл модуля производной:
в
точке ω0
к образу
этой кривой Г/.
Геометрический
смысл модуля производной:
 - модуль производной функции
в точке Z0
геометрически равен коэффициенту
растяжения в точке Z0
при отображении ω = f(z).
- модуль производной функции
в точке Z0
геометрически равен коэффициенту
растяжения в точке Z0
при отображении ω = f(z).
Линейная функция
 a,
b
a,
b
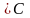 ,
,
 т.е.
т.е.

 . Так как
. Так как
 ,
то имеем, что
,
то имеем, что




 .
Следовательно,
.
Следовательно,
 ,
,
 .
.
1)
–
аналитическая функция, т.е. u
и v
– гармоническая
пара, т.к. выполняются условия КРЭДа:
 ,
,
 .
.
2)
 для всех z
.
для всех z
.
Из 1) и 2) следует, что отображение, реализуемое линейной функцией, конформно на всей плоскости Гаусса. Вывод:
Отображение,
осуществляемое линейной функцией,
представляет собой композицию растяжения
 ,
поворота
,
поворота
 и параллельного переноса
и параллельного переноса

Простейшая дробно-линейная функция
 – аналитическая
функция, т.к. выполняются условия КРЭДа.
– аналитическая
функция, т.к. выполняются условия КРЭДа.
 ни при каком конечном
z
(лишь при
ни при каком конечном
z
(лишь при
 ).
Следовательно, производная существует
всюду, кроме z
= 0.
).
Следовательно, производная существует
всюду, кроме z
= 0.
Отображение,
реализуемое функцией, конформно всюду
на (z),
кроме точки z
= 0 и бесконечно удаленной точки
.
Если положить
 ,
то отображение будет конформно во всей
плоскости (z).
При этом угол между прямыми в точке О
отображается на такой же угол в бесконечно
удаленной точке
.
,
то отображение будет конформно во всей
плоскости (z).
При этом угол между прямыми в точке О
отображается на такой же угол в бесконечно
удаленной точке
.
О. Преобразование, переводящее внутренность единичного круга во внешность и наоборот, называется инверсией.
Вывод: При отображении, реализуемом функцией , происходит инверсия: внутренность единичного круга отображается в его внешность и наоборот, при одновременном симметрическом отображении относительно оси (Ох).
Степенная функция
 , z
≥ 2.
–
аналитическая функция на всей плоскости
Гаусса:
, z
≥ 2.
–
аналитическая функция на всей плоскости
Гаусса:
 кроме z
= 0. Следовательно, отображение, задаваемое
функцией конформно всюду, кроме начала
координат.
кроме z
= 0. Следовательно, отображение, задаваемое
функцией конформно всюду, кроме начала
координат.
Запишем комплексное
число z
тригонометрической форме
 .
Тогда
.
Тогда
 (формула Муавра).
(формула Муавра).
У степенной
функций сектор раствором
 плоскости
(z)
конформно отображается на всю плоскость
(
плоскости
(z)
конформно отображается на всю плоскость
( ).
).
