
- •Понятия фкп. Выражения для х и у.
- •Основные Элементарные функции
- •Предел и непрерывность фкп
- •Дифференцируемость. Условие Коши-Римана
- •Гармонические функции. Гармонические пары.
- •Определение и св-ва аналитических функций
- •Конформность отображения посредством гармонической пары и аналитической функции. Геометрический смысл модуля и аргумента производной.
- •Линейная функция
- •Простейшая дробно-линейная функция
- •Степенная функция
- •Дробно-линейная функция
- •Интегрирование по комплексному аргументу
- •Теорема Коши. Интегральная формула Коши
- •Ряды с комплексными членами
- •Изолированные особые точки и их классификация
- •Ряд Тейлора
- •Ряд Лорана
- •Основные теоремы о вычетах
- •Скалярное поле. Определение. Линии и поверхности уровня.
- •Скалярное поле. Производная по направлению.
- •Скалярное поле. Градиент
- •Векторное поле. О. Векторные линии и векторные трубки
- •Поток векторного поля. О. Вычисление.
- •Дивергенция векторного поля. О. Выч. Теорема г-о
- •Циркуляция векторного поля. О. Вычисление
- •Ротор векторного поля. О. Выч. Теорема Стокса
- •Оператор Гамильтона. Диф-ые операции II порядка
- •Специальные виды векторных полей. Соленоидальое
- •Специальные виды векторных полей. Потенциальное
- •Специальные виды векторных полей. Лапласово (гармоническое)
- •Теорема о разложении векторных полей.
- •Применение вычетов к вычислению контурных интегралов
- •Применение тфкп
- •Определение функционального анализа. Предмет функционального анализа.
- •Определение евклидова пространства
- •Определение линейных пространств. Аксиомы. Свойства
- •Линейные операторы. Действия с лин. Операторами
- •Базис и матрица линейного оператора Собственные значения и собственные векторы линейного оператора
- •Квадратичные формы. Матрица квадратичной формы. Пример.
- •Ортогональный и ортонормированный базис
- •Понятие меры. Измеримые функции. Простые функции. Ортогональные функции
- •Мера Лебега. Свойства меры Лебега. Интеграл Лебега
- •Нормированные пространства. Норма. Примеры
- •Метрические пространства. Метрика. Примеры. Сжатые отображения
- •Ортогональный и ортонормированный базис. Процесс Ортогонализации. Сопряженные векторы в евклидовом пространстве.
- •Дифференциальные уравнения с частными производными
- •Основные уравнения математической физики
- •Явная и Неявная разностная схема
Дробно-линейная функция
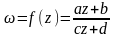 , ad–bc
≠ 0, a,b,c,d
.
может
быть приведена к виду
, ad–bc
≠ 0, a,b,c,d
.
может
быть приведена к виду
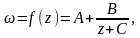 где
где
 .
.
–
аналитическая во
всей расширенной плоскости Гаусса,
кроме
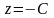 .
Если принять, что
.
Если принять, что
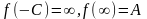 ,
и углы между кривыми при переходе от
точки
к точке Z
=
,
и углы между кривыми при переходе от
точки
к точке Z
=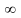 и наоборот равны, то отображение будет
конформно во всей расширенной плоскости
Гаусса.
и наоборот равны, то отображение будет
конформно во всей расширенной плоскости
Гаусса.
Дробно-линейная
функция
вполне определяется заданием образов
трех точек. Например, если
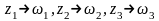 ,
то
,
то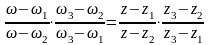 .
.
Интегрирование по комплексному аргументу
О.
Если существует
конечный предел интегральной суммы
при
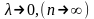 ,
который не зависит ни от способа
разбиения дуги на элементарные дуги,
ни от выбора на них точек
,
который не зависит ни от способа
разбиения дуги на элементарные дуги,
ни от выбора на них точек
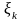 ,
то он называется интегралом от функции
по
дуге кривой l
и обозначается
,
то он называется интегралом от функции
по
дуге кривой l
и обозначается
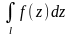 .
Т
(существования).
Если функция
непрерывна
на l
, то интеграл от нее по дуге l
существует. Формула для вычисления
интеграла:
.
Т
(существования).
Если функция
непрерывна
на l
, то интеграл от нее по дуге l
существует. Формула для вычисления
интеграла:
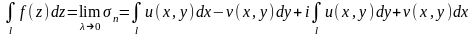 .
.
Свойства:
1.
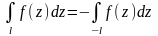 .
2.
.
2.
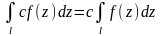 .
.
3.
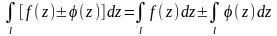 .
4.
.
4.
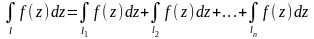 ,
,
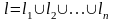 .
5.
.
5.
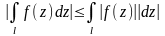 .
6. Если
–
аналитическая функция, то интеграл
не зависит от пути интегрирования l.
.
6. Если
–
аналитическая функция, то интеграл
не зависит от пути интегрирования l.
Теорема Коши. Интегральная формула Коши
Т.
(т. Коши). Если
функция ω = f(z)
однозначная аналитическая функция в
односвязной области D,
ограниченной контуром L
и l
–замкнутый контур в области D,то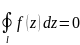 .
Если, дополнительно, функция ω = f(z)
– непрерывна в замкнутой области
.
Если, дополнительно, функция ω = f(z)
– непрерывна в замкнутой области
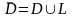 ,
то
,
то
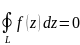 .
Доказательство.
.
Доказательство.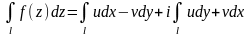 .
В силу аналитичности функции
функции u(x,y)
и v(x,y)
образуют гармоническую пару, для которой
справедлива т. Коши:
.
В силу аналитичности функции
функции u(x,y)
и v(x,y)
образуют гармоническую пару, для которой
справедлива т. Коши:
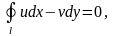
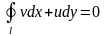 .
Следовательно,
.
Следовательно,
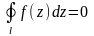 ,
ч.т.д.
,
ч.т.д.
Т.
(интегральная формула Коши).
Значение функции ω = f(z),
аналитической в односвязной области
D,
в особой точке
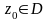 определяется ее значениями на любом
замкнутом кусочно-гладком контуре l,
охватывающем точку z0
, целиком
лежащем вместе со своей внутренностью
в области D,
и вычисляется по формуле:
определяется ее значениями на любом
замкнутом кусочно-гладком контуре l,
охватывающем точку z0
, целиком
лежащем вместе со своей внутренностью
в области D,
и вычисляется по формуле:
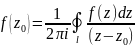 .
При этом функция ω = f(z)
имеет всюду в D
производные любого порядка, для кот.
справедливы ф-лы:
.
При этом функция ω = f(z)
имеет всюду в D
производные любого порядка, для кот.
справедливы ф-лы:
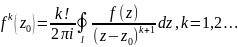
Ряды с комплексными членами
Рассмотрим
последовательность комплексных чисел
 ,
n
= 1,2,…
,
n
= 1,2,…
О.
Последовательность комплексных чисел
Z
n
называется сходящейся, а число z=x+iy
ее пределом
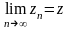 ,
если существуют конечные пределы
,
если существуют конечные пределы
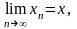
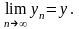
О.
Числовым рядом с комплексными членами
называется составленное из
последовательности комплексных чисел
выражение:
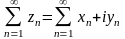 .
Частичной суммой ряда называется
выражение Sn
=
.
Частичной суммой ряда называется
выражение Sn
=
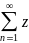 n
= z1
+ z2
+…+ zn..
О.
Ряд
n
называется
сходящимся, если существует конечное
число S
такое, что
n
= z1
+ z2
+…+ zn..
О.
Ряд
n
называется
сходящимся, если существует конечное
число S
такое, что
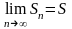 ,
где S
– сумма ряда. Так как
S
– комплексное
число, то S
= u
+iv.
,
где S
– сумма ряда. Так как
S
– комплексное
число, то S
= u
+iv.
Необх. и дост.
условие сходимости:
ряд
n
=
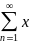 n
+ iyn
сходится к сумме S
= u
+ iv
тогда и
только тогда, когда сходятся в отдельности
ряды из действительных и мнимых частей
его членов и выполняются равенства:
n
= u,
n
+ iyn
сходится к сумме S
= u
+ iv
тогда и
только тогда, когда сходятся в отдельности
ряды из действительных и мнимых частей
его членов и выполняются равенства:
n
= u,
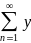 n
= v.
О.
Ряд
n
называется
абсол. cход.,
если сходится ряд из модулей членов
данного ряда
n
= v.
О.
Ряд
n
называется
абсол. cход.,
если сходится ряд из модулей членов
данного ряда
 zn|.
zn|.
