Основные теоремы о вычетах

Т. (первая теорема о вычетах, или основная) Если функция f(z) аналитическая в области D, за исключением изолированных особых точек Z₁,Z₂,…,Z_N, лежащих внутри этой области, то для любого простого замкнутого контура Г , охватывающего точки Z₁,Z₂,…,Z_N, интеграл равен произведению (2πi) на сумму вычетов относительно особых точек f(z), лежащих внутри контура Г:

Доказательство. Z₁,Z₂,…,Z_N – особые точки, лежащие внутри контура. Обозначим как α₁ = re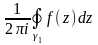s , α₂ = res , … ,

α_N = res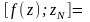 , где - контуры – окружности вокруг этих точек, лежащие внутри Г и вне друг друга. Следовательно, по теореме Коши для сложного контура (для многосвязной области) можно записать, что

= 2πi [α₁ + α₂ + …+ α_N] =

= = , что и требовалось доказать.

Т. (вторая теорема о вычетах) Если функция f(z) аналитическая во всей комплексной плоскости, за исключением изолированных особых точек , то сумма всех вычетов относительно особых точек f(z) равна нулю^: _k]=0

Скалярное поле. Определение. Линии и поверхности уровня.

О. Если в области V₁ задана скалярная функция точки u (P),то говорят, что в этой области задано скалярное поле. Пример:поля температуры, атмосферного давления и т.п.

О. Если функция u (P) не зависит от времени, то скалярное поле называют стационарным. Поле, меняющееся с течением времени называется нестационарным.

О. Поверхностью уровня пространственного скалярного поля или изоповерхнотью называется геометрическое место точек, в которых функция u принимает постоянное значение: u(x,y,z)=C. Поверхности уровня могут вырождаться в линии и точки.

О. Линии, во всех точках которых плоское скалярное поле имеет одно и то же значение, называются линиями уровня или изолиниями. Линии уровня могут вырождаться в точки.

Пример линий уровня: изотерма, изохора, изобара.

Скалярное поле. Производная по направлению.

О. Производной функции u=u(P) в точке P по направлению ʎ вектора ʎ называется предел:

Производная по направлению характеризует скорость изменения в точке Р по направлению вектора . Если , то функция возрастает в направлении . Величина представляет собой мгновенную скорость изменения функции u в направлении вектора

в точке Р. Теорема. Если функция u(P) = u(x,y,z) дифференцируема то ее производная по любому направлению вектора существует и равна:

где cosα, cosβ, cosγ – направляющие косинусы .

Направляющие косинусы находятся по формулам:

Скалярное поле. Градиент

О. Градиентом функции u=u(x,y,z) называется вектор, проекциями которого служат значения частных производных этой функции:

Градиент функции указывает направление

наибыстрейшего возрастания функции.

Т. Направление градиента функции u=u(x,y,z) в каждой точке совпадает с направлением нормали к поверхности уровня скалярного поля, проходящей через это точку. Док-во.

Выберем произвольную точку P₀(x₀,y₀,z₀). Уравнение поверхности уроввня,

проходящей через точку P₀: u(x,y,z)=C, где С=u(x₀,y₀,z₀). Ур-ие нормали

к пов-тив точке Р₀:

где - координаты направляющего вектора нормали

По определению градиента вектор n есть градиент функции

u=u(x,y,z) в точке Р₀ (ч.т.д.)

Формула для нахождения косинуса угла между векторами: cosφ=