
- •2.)Признаки сравнения рядов:
- •4).Функциональные ряды.
- •3).Знакочередующиеся ряды
- •5.Непрерывность суммы функционального ряда .
- •6.Степенные ряды
- •7.Непрерывность суммы функционального ряда. Почленноедифференцированиеи интегрирование.
- •8)Ряды тейлора
- •9)Применение рядов к реш-ю диф-ыхур-й, выч-е опред-ых интегралов(некоторые применения степенных рядов)
- •10)Тригонометрический ряд Фурье. Достаточное условие сходимости
- •§ 1. Тригонометрическая система функций
- •13)Основные понятия и определения ду
- •14)Теорема сущ-ния единственности кошидлядифур-я 1-го порядка
- •16) Линейные уравнения
- •17)Уравнения в полных дифференциалах
- •18)Уравнения высшего порядка основные понятия и определения
- •19. Уравнения, допускающие понижения порядка.
- •21)Линейные дифференциальные уравнениявысших порядков
- •25. Линейные однородные уравнения с постоянными коэффициентами
- •26. Линейные неоднородные дифференциальные уравнения с постояннымикоэффициентамии специальной правой частью
- •29)Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •31. Основные понятия теории устойчивости
- •33.Устойчивость нелинейных систем по первому приближению
- •35. Преобразования Лапласа и его св-ва.
- •37.Применение преобразование Лапласа к решению дифференциальных уравнений и систем
- •39. Приведение лу в частных производных второго порядка к каноническому виду.
- •40. Вывод основных уравнений математической физики
- •41. Метод Фурье решение волнового уравнения
35. Преобразования Лапласа и его св-ва.
Оригинал – комплекснозначная функция f(t) действительного переменного t удовлетворяющего следующим условиям:
1)f(t)=0 при t<0
2)f(t) интегр-емая функция на любом конечном интервале оси Ot
3)с возрастанием t, модуль функции растет не быстрее некоторой показательной функции,
т.е.
m>0
, S
̥≥0 что │f(t)│≤m*![]()
s ̥- показатель роста f(t)
ФункциюF(p) наз-ют изображением функции f(t) по Лапласу если выполняется равенство:
F(p)=![]()
Св-ва.
1)Линейность. Для любых комплексных постоянных α и β αf(t)+βg(t)=αF(p)+βG(p), т.е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.
2)Подобие.
Для любого постоянного α>0 f(αt)=![]() ,
т.е. умножение аргумента оригинала на
положительное число α приводит к делению
изображения аргумента на это число.
,
т.е. умножение аргумента оригинала на
положительное число α приводит к делению
изображения аргумента на это число.
3)Смещение.
Для комплексного числа α ![]() ,
т.е. умножение оригинала на функцию
,
т.е. умножение оригинала на функцию ![]() влечет за собой смещение переменной p.
влечет за собой смещение переменной p.
4)Запаздывание.
Для любого τ>0 имеем f(t-τ)=![]() ,
т.е. запаздывание оригинала на положительную
величину τ приводит к умножению
изображения оригинала без запаздывания
на
,
т.е. запаздывание оригинала на положительную
величину τ приводит к умножению
изображения оригинала без запаздывания
на![]() .
.
5)Дифференцирование
оригинала. Если функции f´(t),f´´(t),…,![]() являются оригиналами и f(t),f´(t),…,
являются оригиналами и f(t),f´(t),…,![]() (t)
непрерывны, то
(t)
непрерывны, то
f´=pF(p)-f(0),
f´´(t)=![]() F(p)
-pf(0)
- f´(0),
F(p)
-pf(0)
- f´(0),
f´´´(t)=![]() -
f(0)
– pf´(0)
- f´´(0),
-
f(0)
– pf´(0)
- f´´(0),
……………………………………………………………
![]() (t)=
(t)=![]() F(p)
-
F(p)
- ![]() f(0)
- … -
(0).
f(0)
- … -
(0).
6)Дифференцирование изображения. Дифференцированию изображения соответствует умножение его оригинала на -t , т.е. F´(p)=-tf(t).
7)Интегрирование
оригинала. ![]() ,
т.е. интегрирование оригинала от 0 до t
соответствует деление его изображения
на p.
,
т.е. интегрирование оригинала от 0 до t
соответствует деление его изображения
на p.
8)Интегрирование
изображения. ![]() , т.е. интегрированию изображения от
pдо
соответствуетделение его оригинала на
t.
, т.е. интегрированию изображения от
pдо
соответствуетделение его оригинала на
t.
9)Умножение изображений.
F(p)*G(p)=![]() g(t-τ)
dτ
g(t-τ)
dτ
10) Умножение оригиналов.
f(t)*g(t)=![]() .
.
36. Формулы обращения. Теоремы разложения.
Теоремы разложения.
1)Если функция F(p) в окрестности точки p= может быть представлена в виде ряда Лоренца
![]()
То
функция f(t)=![]() (t>0)
является оригиналом, имеющим изображение
F(p),
(t>0)
является оригиналом, имеющим изображение
F(p),
F(p)=![]()
2)Если
F(p)=![]() – правильная рациональная дробь,
знаменатель которой
– правильная рациональная дробь,
знаменатель которой![]() имеет
лишь простые корни (нули)
имеет
лишь простые корни (нули) ![]() ,
,
![]() ,…,
,…,
![]() ,
то функция f(t)=
,
то функция f(t)=![]() является оригиналом, имеющим изображение
F(p).
является оригиналом, имеющим изображение
F(p).
Формулы обращения.
3)Формула Меллина. Не только f(x) определяет F(p), но и наоборот. Это соответствие задается формулой обращения:
f(x)=![]()
4)Формула Римана-Меллина. Изображение функции может быть найдено по формуле:
f(t)=![]()
37.Применение преобразование Лапласа к решению дифференциальных уравнений и систем
Пусть дано линейное дифференциальное уравнение с постоянным коэффициентом:
![]() (1)
(1)
И пусть ищется его решение, удовлетворяющее начальным условиям :
![]() (2)
(2)
Применим
к уравнению (1) преобразование
Лапласа:
-Преобразование
Лапласа функции У. Интегрируем по частям,
мы найдём преобразование Лапласа
производной У`:
![]()
Применяя эту формулу, найдём:
![]()
Пусть, наконец,
В итоге преобразование Лапласа переводит дифф-ное уравнение (1) с учётом условий (2) в алгебраическое уравнение:
Где В-преобразование Лапласа функции b, Q-многочлен от рстепени n-1, зависящий от коэффициентов уравнения и от начальных данных. Наконец:
Характеристический многочлен уравнения
Функцией-оригиналом называется комплекснозначная функция f(t) действительного переменного t , удовлетворяющая следующим условиям
1)![]() ,
если t<0;
,
если t<0;
2) функция f(t) интегрируема на любом конечном интервале оси ;
3)
с возрастанием t
модуль функции f(t)
растет не быстрее некоторой показательной
функции, т. е. существуют числа M>0
и
![]() такие, что для всех t
имеем
такие, что для всех t
имеем
![]() (1)
(1)
Изображением
функции-оригинала по Лапласу называется
функция F(p)
комплексного переменного![]() , определяемая равенством
, определяемая равенством
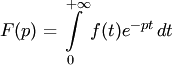 (2)
(2)
при![]() . Условие 3 обеспечивает существование
интеграла (2).
. Условие 3 обеспечивает существование
интеграла (2).
Преобразование
(2), ставящее в соответствие оригиналу
f(t)
его изображениеF(t)
, называется преобразованием Лапласа.
При этом пишут .![]()
38.Классификация уравнений математической физики. Значительная часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:
![]() ,
(1)
,
(1)
где все коэффициенты aij (aij = aij), bi, с и правая часть f представляют собой заданные функции независимых переменных x1, x2,..., хп (n ≥ 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно λ) уравнения
![]() = 0, (2)
= 0, (2)
и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все n корней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты aij постоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x1,..., хп, то и корни уравнения (2) зависят от x1,..., хп, а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).
Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.
