
- •K 2. Теорема Кронекера — Капелли
- •5. Кривая второго порядка
- •6. Поверхность второго порядка
- •Типы поверхностей второго порядка Цилиндрические поверхности
- •Поверхности вращения
- •Гиперболический параболоид («седло»).
- •Центральные поверхности
- •Предел функции по Гейне
- •Предел функции по Коши
- •Бесконечно малая величина
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Теорема
- •14. Предельный переход в неравенствах
- •16. Первый замечательный предел:
- •17. Второй замечательный предел
- •18. Непрерывность функции в интервале и на отрезке
- •19. Точки разрыва функции и их классификация
- •22. Понятие производной ф-ции. Непрерывность ф-ции, имеющей производную.
- •23. Понятие дифференцируемости функции.
- •24. Производная обратной функции.
- •25. Производная сложной функции.
- •26. Производная параметрически заданной функции.
- •27. Производная произведения двух функций.
- •28. Производная частного двух функций.
- •29. Теорема Роля.
- •30. Теорема Ла-Гранжа.
- •31. Теорема Коши.
- •32. Правило Лопиталя.
- •33. Экстремумы функций одной переменной (точки мах и мин).
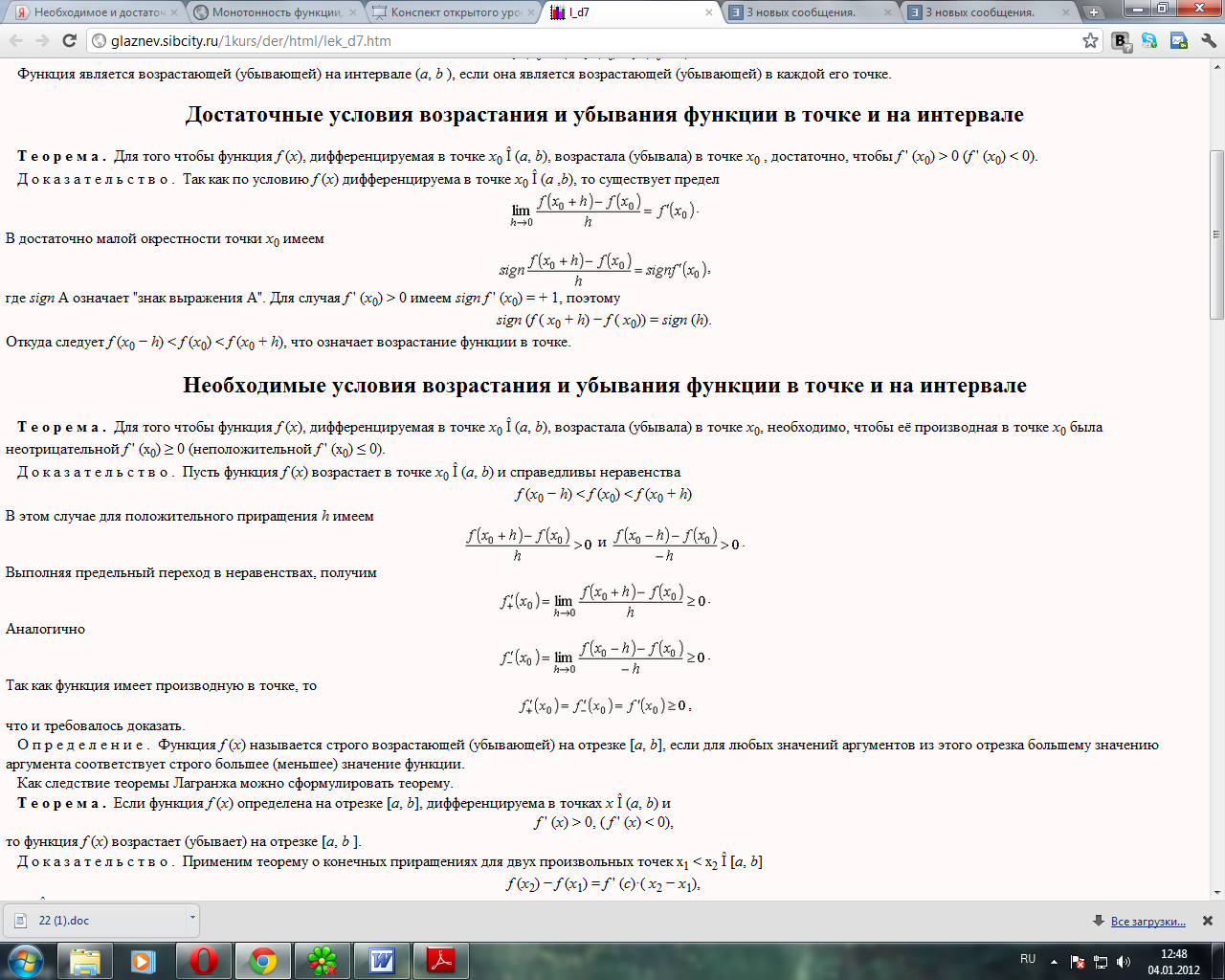
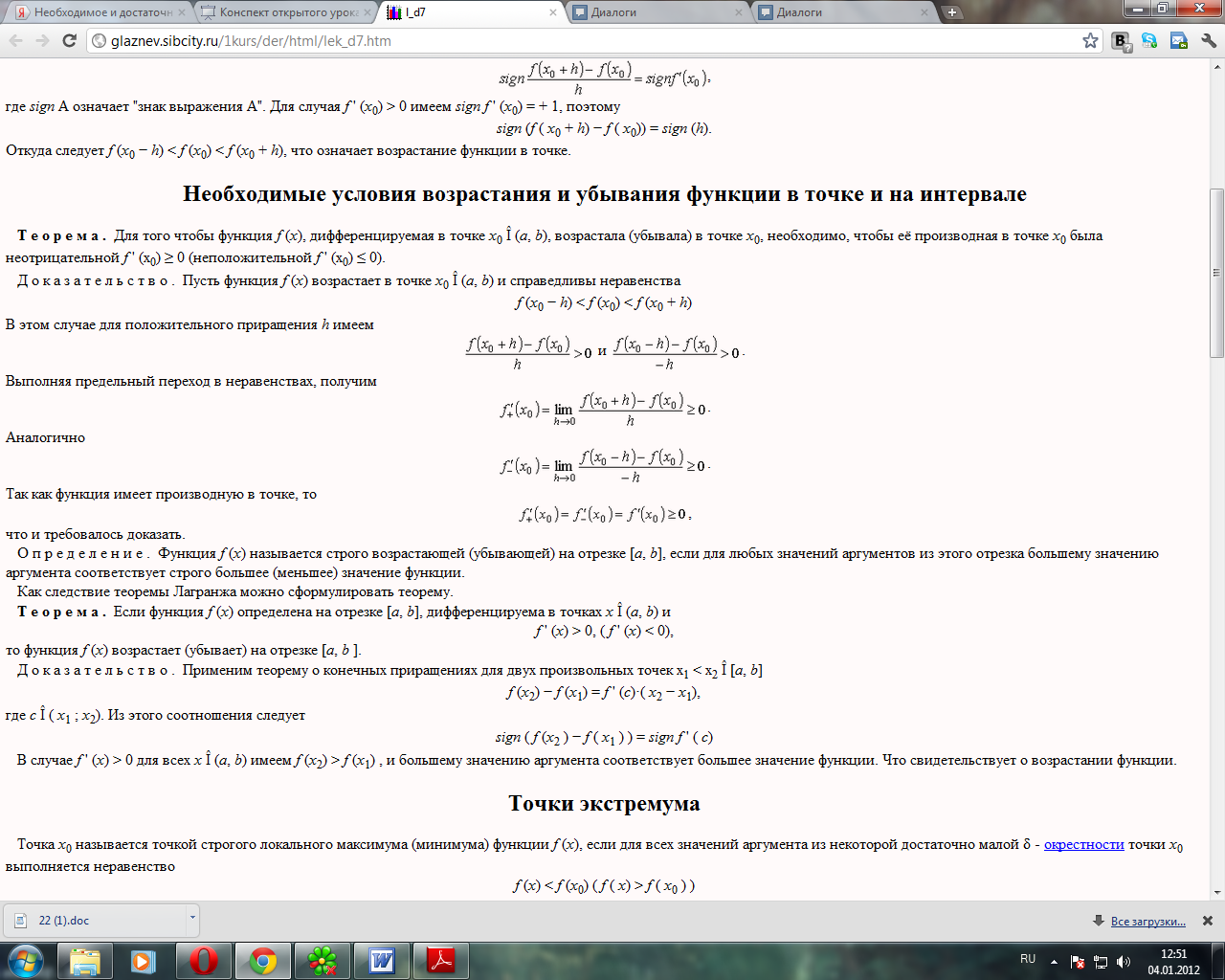
- •34. Необходимое и достаточное условие монотонности функции.
- •35. Необходимое, достаточное условие экстремума
- •2. Достаточное условие экстремума.
- •36. Выпуклость, вогнутость функции. Точки экстремума.
- •37. Асимптоты.
- •38. Общая схема исследования функции одной переменной.
- •39. Частные производные и диффер. Функции нескольких переменных.
- •40. Производная от сложной функции нескольких переменных.
- •41. Производная неявно заданной функции.
- •42.Производная по направлению. Градиент.
- •43.Касательная плоскость. Нормаль к поверхности.
- •44. Необходимые, достаточные условия существования экстремума функции нескольких переменных.
31. Теорема Коши.
Если функции ƒ(х) и φ(x) непрерывны на отрезке [a;b], дифференцируемы на интервале (α;b), причем φ'(х)¹ 0 для хє(а;b), то найдется хотя бы одна точка сє(a;b) такая, что выполняется равенство
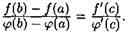
Отметим, что φ(b)—φ(а)≠0, так как в противном случае по теореме Ролля нашлась бы точка с, такая, что φ'(с)=0, чего не может быть по условию теоремы. Рассмотрим вспомогательную функцию
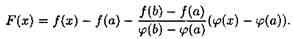 , следовательно,
, следовательно,
![]()
Отсюда следует
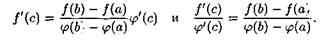
32. Правило Лопиталя.
1. Правило Лопиталя раскрытия неопределенностей вида 0/0.
Пусть функции ƒ(х) и φ(x) непрерывны и дифференцируемы в окрестности точки х0 и обращаются в нуль в этой точке: ƒ(х0)=φ(х0)=0. Пусть φ'(х)¹ 0 в окрестности точки х0. Если существует предел
![]()
Применим к функциям ƒ(х) и φ(х) теорему Коши для отрезка [х0;х], лежащего в окрестности точки x0 . Тогда
![]()
где с лежит между х0 и х (рисунок см). Учитывая, что ƒ(х0)=φ(х0)=0, получаем

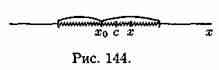
При х→х0, величина с также стремится к х0; перейдем в этом равенстве к пределу:
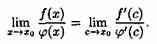
Так как

Поэтому
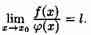
Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Пример:

2. Правило Лопиталя раскрытия неопределенностей вида ∞/∞.
Пусть функции ƒ(х) и φ(х) непрерывны и дифференцируемы в окрестности точки х0 (кроме, может быть, точки х0). в этой окрестности
![]()
φ'(х)¹ 0. Если существует предел
![]()
Пример :
1 способ
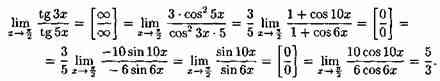
2 способ
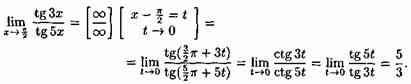
33. Экстремумы функций одной переменной (точки мах и мин).
Точка х0 называется точкой максимума функции у=ƒ(х), если существует такая d -окрестность точки х0, что для всех х≠х0 из этой окрестности выполняется неравенство ƒ(х)<ƒ(х0).
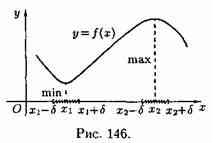
Аналогично определяется точка минимума функции: x0 — точка минимума функции, если $d >0 " х: 0<|x-x0|<d Þ ƒ(х)>ƒ(х0). На рисунке 146 х1 — точка минимума, а точка х2 — точка максимума функции у=ƒ(х).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.
34. Необходимое и достаточное условие монотонности функции.
35. Необходимое, достаточное условие экстремума
1. Необходимое условие экстремума
Если дифференцируемая функция у=ƒ(х) имеет экстремум в точке х0, то ее производная в этой точке равна нулю: ƒ'(х0)=0.
Пусть, для определенности, x0 — точка максимума. Значит, в окрестности точки х0 выполняется неравенство ƒ(х0)>ƒ(х0+∆х). Но тогда
![]() если ∆х>0, и
∆у/∆х>0, если ∆х<0.
если ∆х>0, и
∆у/∆х>0, если ∆х<0.
По условию теоремы производная
![]()
существует. Переходя к пределу, при ∆х→0, получим ƒ'(x0)≥0, если ∆х<0, и f'(х0)≤0, если ∆х>0. Поэтому ƒ'(х0)=0. Аналогично доказывается утверждение теоремы 25.8, если х0 — точка минимума функции ƒ(х).
Геометрически равенство ƒ'(х0)=0 означает, что в точке экстремума дифференцируемой функции у=ƒ(х) касательная к ее графику параллельна оси Ох (см. рис.).
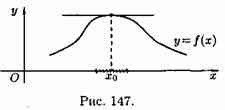
Отметим, что обратная теорема неверна, т. е. если ƒ'(х0)=0, то это не значит, что х0- точка экстремума. Например, для функции у=х3 ее производная у'=3х2 равна нулю при х=0, но х=0 не точка экстремума (см. рис.).
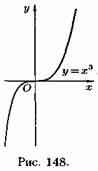
Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция у=׀ х׀ в точке х=0 производной не имеет, но точка х=0 — точка минимума (см. рис.).
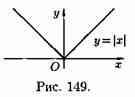
Таким образом, непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.
