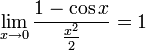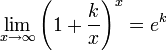16. Первый замечательный предел:
Доказательство
Рассмотрим
односторонние пределы
и
и докажем, что они равны 1.
Пусть
.
Отложим этот угол на единичной окружности
(R
= 1).
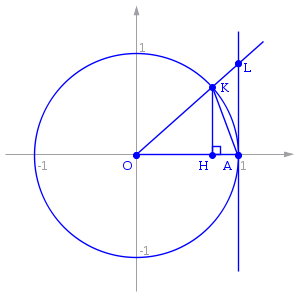
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
(1) (где SsectOKA —
площадь сектора OKA)
(из
:
| LA
| = tgx)
Подставляя в (1), получим:
Так как при
:
Умножаем на sinx:
Перейдём к пределу:
Найдём левый односторонний предел:
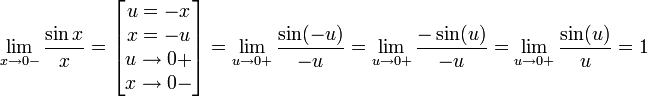
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
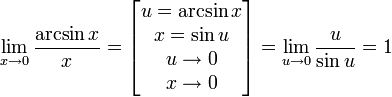
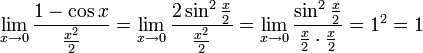
17. Второй замечательный предел
или
Доказательство второго замечательного предела:
Докажем
вначале теорему для случая последовательности
По
формуле бинома
Ньютона:
Полагая
,
получим:
(1)
Из
данного равенства (1) следует, что с
увеличением n число положительных
слагаемых в правой части увеличивается.
Кроме того, при увеличении n число
убывает,
поэтому величины
возрастают.
Поэтому последовательность
—
возрастающая,
при этом
(2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
.
Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:
.
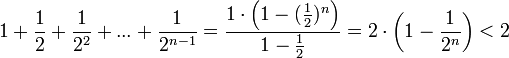Поэтому
(3).
Итак,
последовательность ограничена сверху,
при этом
выполняются
неравенства (2) и (3):
.
Следовательно,
на основании теоремы Вейерштрасса
(критерий сходимости последовательности)
последовательность
монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е.
Зная, что второй
замечательный предел верен для натуральных
значений x, докажем второй замечательный
предел для вещественных x, то есть
докажем, что
.
Рассмотрим два случая:
1. Пусть
.
Каждое значение x заключено между двумя
положительными целыми числами:
,
где
—
это целая часть x.
Отсюда следует:
,
поэтому
.
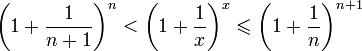Если
,
то
.
Поэтому, согласно пределу
,
имеем:
.
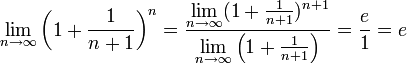
По признаку (о
пределе промежуточной функции)
существования пределов
.
2. Пусть
.
Сделаем подстановку −
x
= t,
тогда
.
Из двух этих случаев вытекает, что для вещественного x.
Следствия
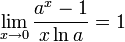для
,
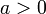18. Непрерывность функции в интервале и на отрезке
Функция у=ƒ(х) называется непрерывной в интервале (a,b), если она непрерывна в каждой точке этого интервала.
Функция у=ƒ(х)
называется непрерывной на отрезке
[а,b], если она непрерывна в интервале
(a,b) и в точке х=а непрерывна справа (т.е.
),
а в точке x=b непрерывна слева (т. е.
).
Теорема 19.1 . Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).
▼Пусть функция
ƒ(х) и φ(х) непрерывны на некотором
множестве X и x0
— любое значение из этого множества.
Докажем, например, непрерывность
произведения F(x)=ƒ(х)•φ(х). Применяя
теорему о пределе произведения, получим:
Итак,
что
и доказывает непрерывность функции
ƒ(х)•φ(х) в точке х0.
▲
Теорема 19.2 . Пусть функции u=φ(х) непрерывна в точке х0, а функция у=ƒ(u) непрерывна в точке u0=φ(хо). Тогда сложная функция ƒ(φ(х)), состоящая из непрерывных, функций, непрерывна в точке х0.
▼В силу непрерывности
функции u=φ(х)
т. е.при х→х0 имеем u→u0. Поэтому вследствие непрерывности функции у=ƒ(u) имеем:
Это и доказывает, что сложная функция у=ƒ(φ(х)) непрерывна в точке х0. ▲
Теорема 19.3 . Если функция у=ƒ(х) непрерывна и строго монотонна на [a;b] оси (Oх, то обратная функция у=φ(х) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу (без доказательства).
Так, например, функция tgx=sinx/cosx . в силу теоремы 19.1, есть функция непрерывная для всех значений х, кроме тех, для которых cosх=0, т. е. кроме значений х=π/2+πn, nєZ.
Функции arcsinx, arctgx, arccosx, arcctgx, в силу теоремы 19.3, непрерывны при всех значениях х, при которых эти функции определены.
Можно доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
всякая элементарная функция непрерывна в каждой точке, в которой она определена.