K 2. Теорема Кронекера — Капелли

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец b является линейной комбинацией столбцов матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

Достаточность

Пусть . Возьмем в матрице A какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

Следствия

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

4. Решение систем линейных алгебраических уравнений

Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.

Однородные системы

Однородной системой линейных уравнений называется система вида:

Нулевое решение системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Решения однородной системы обладают свойством линейности:

Теорема (о линейном решении однородных систем). Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы.

Теорема (о структуре общего решения). Пусть , тогда:

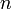• если , где — число переменных системы, то существует только тривиальное решение;

если , то существует линейно независимых решений рассматриваемой системы: , причём её общее решение имеет вид: , где — некоторые константы.

Пусть дана однородная система (1), тогда набор векторов размера называется фундаментальной системой решений (ФСР) (1), если:

• — решения системы (1);

• линейно независимы;

• .

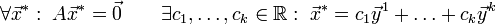Теорема (о ФСР). Пусть ранг основной матрицы , где — число переменных системы (1), тогда:

• ФСР (1) существует: ;

• она состоит из 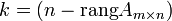векторов;

• общее решение системы имеет вид .

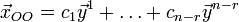Замечание: Если , то ФСР не существует.

Пример

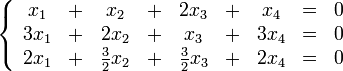
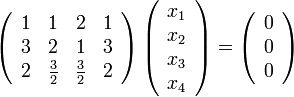
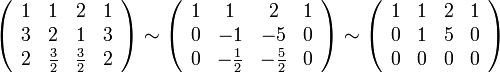
Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует линейно независимых решения системы.

Возьмём и в качестве главных переменных. Тогда:

Подставим по очереди единицы в качестве одной из свободных переменных: и .

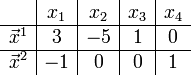
Тогда общее решение рассматриваемой системы может быть записано так:

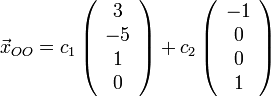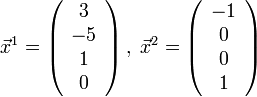, а вектора составляют фундаментальную систему решений.