2. Достаточное условие экстремума.

Если непрерывная функция у=ƒ(х) дифференцируема в некоторой d -окрестности критической точки х0 и при переходе через нее (слева направо) производная ƒ'(х) меняет знак с плюса на минус, то х0 есть точка максимума; с минуса на плюс, то х0 — точка минимума.

Рассмотрим d -окрестность точки х0. Пусть выполняются условия: ƒ'(х)>0 " xє(х0-d ;х0) и ƒ'(х)<0 " xє(х0;х0+d ). Тогда функция ƒ(х) возрастает на интервале (х0-δ; х0), а на интервале (х0; х0+d ) она убывает. Отсюда следует, что значение ƒ (х) в точке x0 является наибольшим на интервале (х0-δ;х0+δ), т. е. ƒ(х)<ƒ(х0) для всех хє(х0-d ;x0)U(x0;x0+d ). Это и означает, что х0 — точка максимума функции.

Графическая интерпретация доказательства теоремы представлена на рисунке.

Аналогично теорема доказывается для случая, когда ƒ'(х)<0 " xє(х0-d ;х0) и ƒ'(х)>0 " xє(х0;х0+d ).

36. Выпуклость, вогнутость функции. Точки экстремума.

1. График функции у=ƒ(х) называется выпуклым на интервале (а;b), если любая точка этой кривой лежит ниже любой касательной, проведенной к данной кривой.

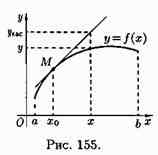
График функции у=ƒ(х) называется вогнутым вниз на интервале (а;b), если любая точка этой кривой лежит выше любой касательной, проведенной к данной кривой.

Точка перегиба – точка кривой данной функции, которая отделяет интервал выпуклости функции от интервала вогнутости.

На рисунке кривая у=ƒ(х) выпукла на интервале (а;с), вогнута на интервале (с;b), точка М(с;ƒ(с)) — точка перегиба.

2.

• Если функция у=ƒ(х) во всех точках интервала (а;b) имеет отрицательную вторую производную, т. е. ƒ"(х)<0, то график функции выпуклый. Если же ƒ"(х)>0 " xє(а;b) — график вогнутый.

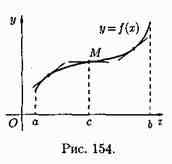
Пусть ƒ"(х)<0 " xє(а;b). Возьмем на графике функции произвольную точку М с абсциссой х0є(а;b) и проведем через М касательную.

Покажем, что график функции расположен ниже этой касательной. Для этого сравним в точке хє(а; b) ординату у кривой у=ƒ(х) с ординатой укас ее касательной. Уравнение касательной, как известно, есть Укас-ƒ(х0)=ƒ'(х0)(х-х0), т.е. Укас=ƒ(х0)+f(x0)(x-х0).

Тогда у-укас=ƒ(х)-ƒ(х0)-ƒ'(х0)(х-х0). По теореме Лагранжа, ƒ(х)-ƒ(х0)=ƒ'(с)(х-x0), где с лежит между х0 и х. Поэтому У-Укас=ƒ'(с)(х-х0)-ƒ'(х0)(х-х0), т. е. У-Укас=(ƒ'(с)-ƒ'(х0))(х-х0).

Разность ƒ'(с)-ƒ'(х0) снова преобразуем по формуле Лагранжа:

ƒ'(с)-ƒ'(х0)=ƒ"(с1)(с-х0), где с1 лежит между х0 и с. Таким образом, получаем

У-Укас=f"(c1)(c-х0)(х-х0).

Исследуем это равенство:

1) если х>х0, то х-х0>0, с-х0>0 и f"(c1)<0. Следовательно, У-Укас<0, т. е. у<укас:

2) если х<х0, то х-х0<0, с-х0<0 и f"(c1)<0. Следовательно, У-Укас<0, т. е. у<укас:

Итак, доказано, что во всех точках интервала (а;b) ордината касательной больше ординаты графика, т. е. график функции выпуклый. Аналогично доказывается, что при ƒ"(х)>0 графиквогнутый.

• Если вторая производная ƒ"(х) при переходе через точку х0, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х0 есть точка перегиба.

37. Асимптоты.

Асимптота прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Асимптоты могут быть вертикальными, наклонными и горизонтальными.

1. Прямая х=а является вертикальной асимптотой графика функции

2. Наклонная асимптота y=kx+b.

Отсюда следует, что kx-у+b=α, где α=α(х) бесконечно малая: α→0 при х→ ∞ . Разделив обе части равенства у=b+kx-α на х и перейдя к пределу при х→ ∞ , получаем:

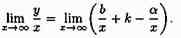
Так как b/х→0 и α/х→0, то

3. Если k=0, то b=limƒ(х) при х →∞ . Поэтому у=b — уравнение горизонтальной асимптоты.

Например: у=хе^х.

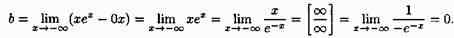
Следовательно, при х→- ∞ график имеет горизонтальную асимптоту у=0.