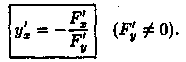38. Общая схема исследования функции одной переменной.

1. Найти область определения функции (множество всех допустимых действительных значений аргумента x).

2. Найти область значений функции (множество всех действительных значений y, которые принимает функция) .

3. Выяснить, является ли функция четной (f(-x) = f), нечетной ((-x) = - f(x)) или общего вида.

4. Переодичность.

5. Точки разрыва функции.

6. Найти асимптоты.

7. Найти интервалы монотонности функции, точки экстремумы (искать нужно производную).

8. Найти интервалы выпуклости и вогнутости, точки перегиба графика функции (вторая производная).

Пример:

1. (-∞;-1), (-1;1), (1;+∞).

2. Если х=0, то у=0. График пересекает ось Оу в точке О(0;0); если у=0, то х=0. График пересекает ось Ох в точке О(0;0).

3. нечетная .

4. непериодичная.

5. 1 и -1

6. Прямые х=1 и х=-1 являются ее вертикальными асимптотами. Выясним наличие наклонной асимптоты:

(k=0 при х→+∞ и при х→-∞),

7. то у'>0 в области определения, и функция является возрастающей на каждом интервале области определения.

Исследуем функцию на экстремум. Так как

то критическими точками являются точки x1=1 и х2=-1 (у' не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.

39. Частные производные и диффер. Функции нескольких переменных.

40. Производная от сложной функции нескольких переменных.

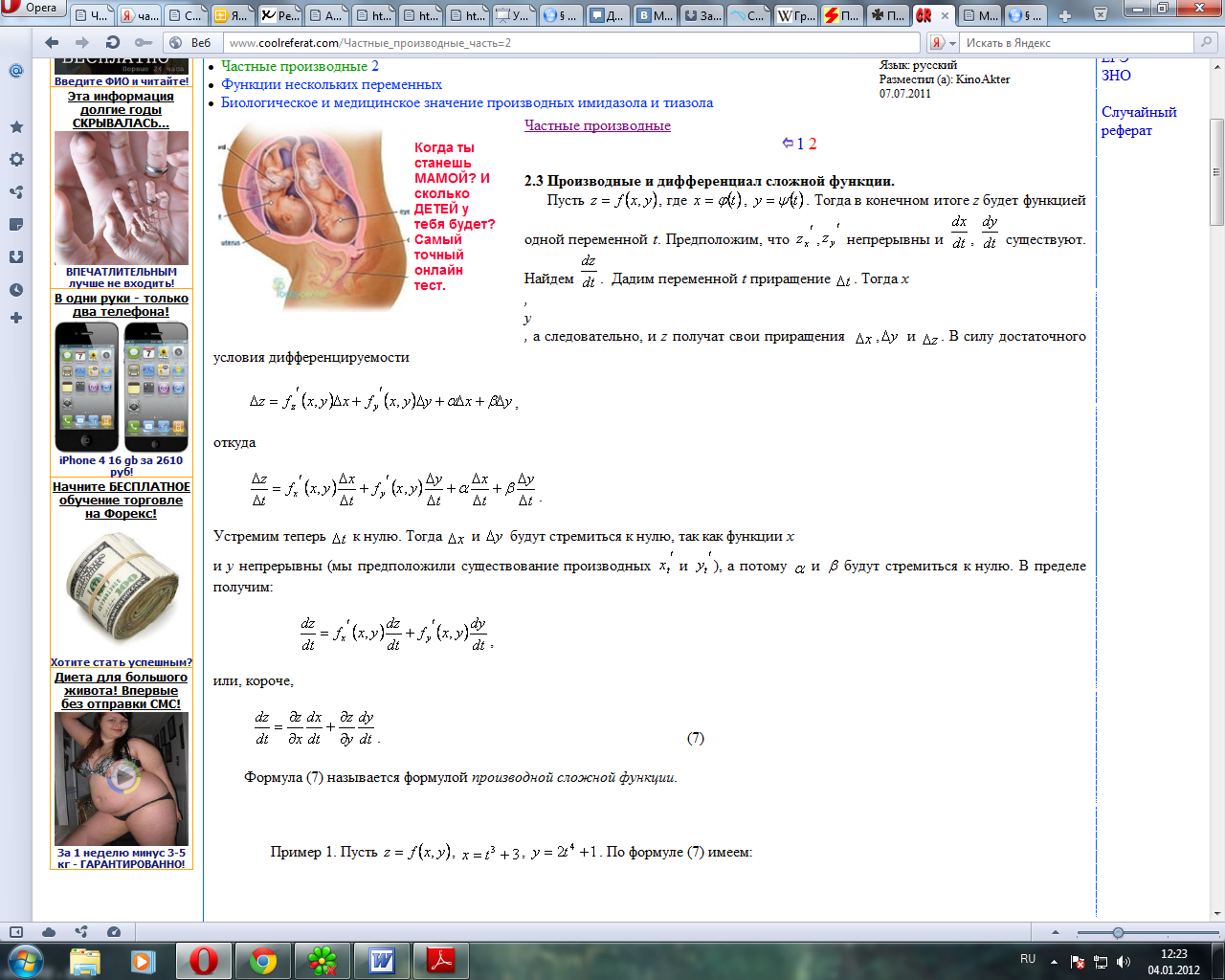
Если z = ƒ(х;у) — дифференцируемая в точке М(х;у) є D функция и х = x(t) и у = y(t) — дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = f(x(t);y(t)) вычисляется по формуле

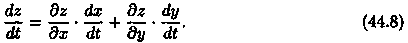
Дадим независимой переменной t приращение Δt. Тогда функции х = = x(t) и у = y{t) получат приращения Δх и Δу соответственно. Они, в свою очередь, вызовут приращение Az функции z.

Так как по условию функция z — ƒ(х;у) дифференцируема в точке М(х; у), то ее полное приращение можно представить в виде

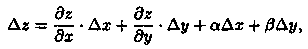где а→0, β→0 при Δх→0, Δу→0 . Разделим выражение Δz на Δt и перейдем к пределу при Δt→0. Тогда Δх→0 и Δу→0 в силу непрерывности функций х = x(t) и у = y(t) (по условию теоремы — они дифференцируемые). Получаем:

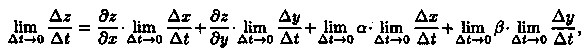
т. е.

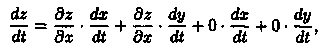
или

Частный случай: z=ƒ(х;у), где у=у(х), т. е. z=ƒ(х;у(х)) — сложная функция одной независимой переменной х. Этот случай сводится к предыдущему, причем роль переменной t играет х. Согласно формуле имеем:

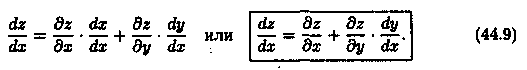
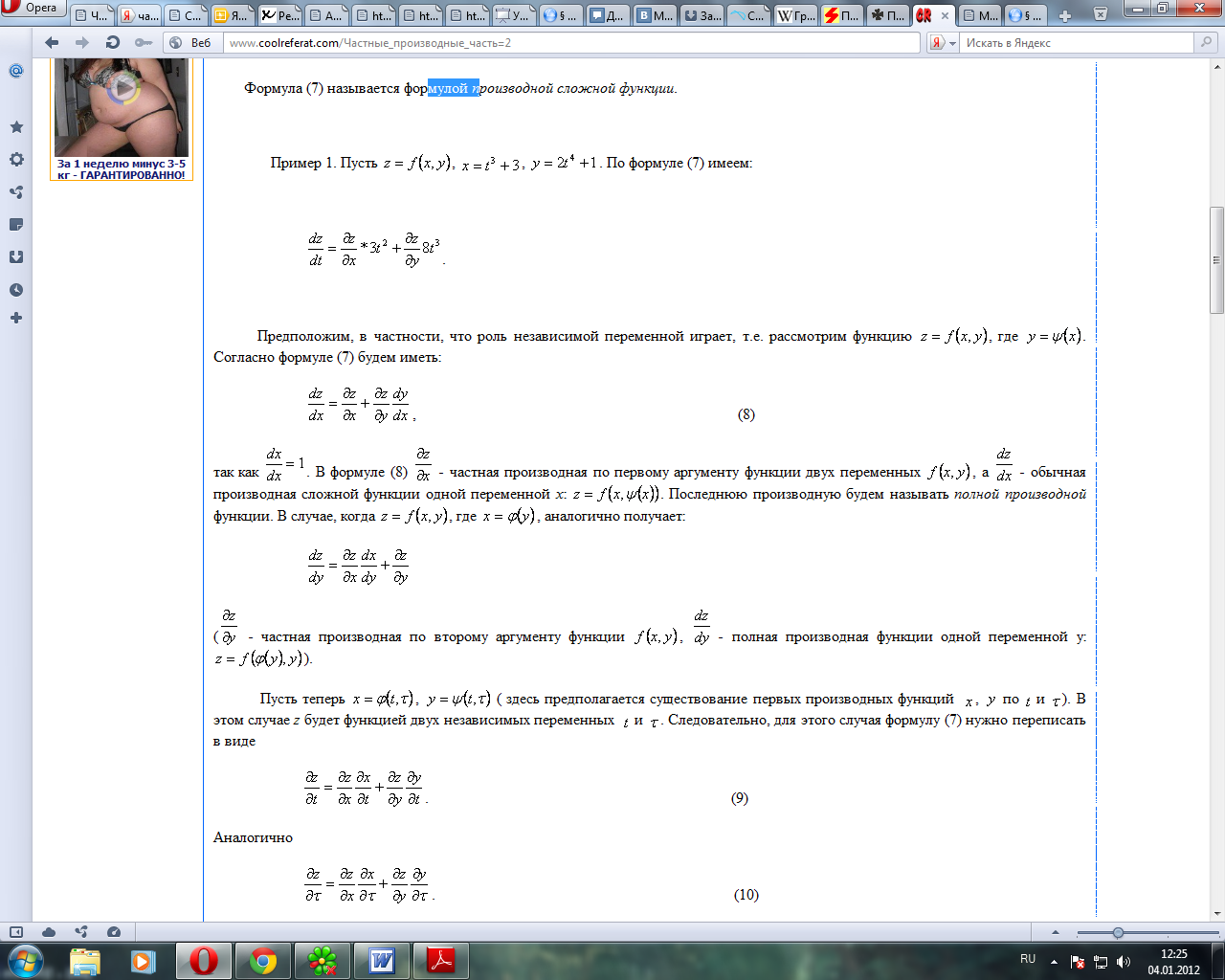
Формула носит название формулы полной производной.

Общий случай: z=ƒ(х;у), где x=x(u;v), у=у(u;v). Тогда z= f(x(u;v);y(u;v)) — сложная функция независимых переменных u и v. Ее частные производные можно найти, используя формулу следующим образом. Зафиксировав v, заменяем в ней соответствующими частными производными

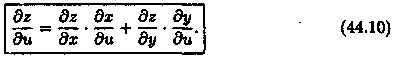
Аналогично получаем:

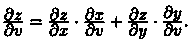
Таким образом, производная сложной функции (z) по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (х и у) на их производные по соответствующей независимой переменной (u и v).

41. Производная неявно заданной функции.

Функция z = ƒ (х; у) называется неявной, если она задается уравнением

неразрешенным относительно z. Найдем частные производные неявной функции z, заданной этим уравнением. Для этого, подставив в уравнение вместо z функцию ƒ (х; у), получим тождество F(x;у;ƒ (х; у)) = 0. Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:

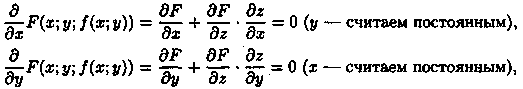
откуда

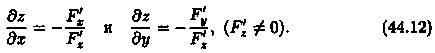
Замечания.

а) Уравнение вида не всегда определяет одну переменную как неявную функцию двух других. Так, уравнение х^2+у^2+z^2-4=0 определяет функции определенные в круге х^2+у^2≤4, определенную в полукруге х^2+у^2 ≤ 4 при у≥ 0 и т. д., а уравнение cos(x + 2у +3z)- 4 = 0 не определяет никакой функции.

Имеет место теорема существования неявной функции двух переменных: если функция F(x; у; z) и ее производные F'x(x; у; z), F'y(x; у; z), F'z(x;y;z) определены и непрерывны в некоторой окрестности точки M0(x0;y0;z0), причем F(x0;y0;z0)=0, а F'z(x0;y0;z0)≠0, то существует окрестность точки М0, в которой уравнение определяет единственную функцию z=ƒ(х;у), непрерывную и дифференцируемую в окрестности точки (х0;у0) и такую, что ƒ(х0;у0)=z0.

б) Неявная функция у=ƒ(х) одной переменной задается уравнением F(x;у)=0. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле