19. Точки разрыва функции и их классификация

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х=х₀ — точка разрыва функции у=ƒ(х), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:

1. Функция определена в окрестности точки х₀, но не определена в самой точке х₀.

Например, функция у1/(x-2)  не определена в точке х₀=2 (см. рис. 120).

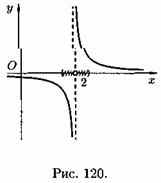
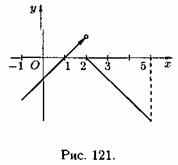
2. Функция определена в точке х₀ и ее окрестности, но не существует предела ƒ(х) при х→х₀. Например, функция

определена в точке х₀=2    (ƒ(2)=0), однако в точке х₀=2 имеет разрыв (см. рис. 121), т. к. эта функция не имеет предела при х→2:

3. Функция  определена в  точке  х₀ и  ее  окрестности,  существует но  этот  предел  не  равен  значению   функции  в  точке x₀:

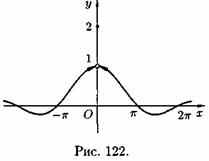
Например, функция (см. рис. 122)

Здесь x₀=0 — точка разрыва:  a g(х₀)=g(0)=2.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Точка разрыва х₀ называется точкой разрыва первого рода функции у=ƒ(х), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е.

 

При этом:

а) если А₁=А₂, то точка х₀ называется точкой устранимого разрыва; б) если А₁≠А₂, то точка х₀ называется точкой конечного разрыва.

Величину |A₁-А₂| называют скачком функции в точке разрыва первого рода.

Точка разрыва х₀ называется точкой разрыва второго рода функции у=ƒ(х), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.

1. Обратимся к функциям, рассмотренным выше (см. рис. 120). у=1/(x-2)  x₀=2 -точка разрыва второго рода.

2. Для функции

х₀=2 является точкой разрыва первого рода, скачок функции равен |1-0|=1.

3. Для функции

х₀=0 является точкой устранимого разрыва первого рода. Положив g(х)=1 (вместо g(х)=2) при х=0, разрыв устранится, функция станет непрерывной

<< Пример 19.3

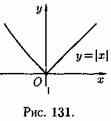
Дана функция ƒ(х)=|x-3|/(x-3). Найти точки разрыва, выяснить их тип.

 Решение: Функция ƒ (х) определена и непрерывна на всей числовой оси, кроме точки х=3. Очевидно,

Следовательно,

Поэтому в точке х=3 функция имеет разрыв пещюго рода. Скачок функции в этой точке равен 1-(-1)=2.

22. Понятие производной ф-ции. Непрерывность ф-ции, имеющей производную.

1. Производной функции f(x) в точке x₀ называется предел отношения приращения функции Δf в этой точке к приращению аргумента Δх, когда последнее стремится к нулю (бесконечно мало). Lim_Δx→0 (Δf(x₀)/Δx)=lim_Δx→0 ((f(x+Δx)-f(x₀))/Δx)=f`(x₀)

Характеризует скорость изменения функции (в данной точке) – физический смысл.

ƒ'(х) = tga = k, производная ƒ'(х) β точке х равна угловому коэффициенту касательной к графику функции у = ƒ(х) в точке, абсцисса которой равна х. В этом заключается геометрический смысл производной.

2. Если функция дифференцируема (имеет производную) в некоторой точке, то она непрерывна в ней (обратное не всегда верно).

Пусть функция у=ƒ(х) дифференцируема в некоторой точке х. Следовательно, существует предел

По теореме о связи функции, ее предела, имеем ∆y/∆x=ƒ'(х)+а, где α→0 при ∆х→0, то есть ∆у=ƒ'(х)•∆х+а•∆х. Переходя к пределу, при ∆х→0, получаем

А это и означает, что функция у=ƒ(х) непрерывна в точке х.

То есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение ф-ции.