9º. Ускорение точки в криволинейных координатах.
Теорема Лагранжа.
Вычислим
ускорение точки 
согласно определению
=
.
Учтем, что
=
=
.
Дифференцируя
правую часть по
,
приходим к векторному представлению
ускорения
в зависимости от вектор-функции
,
обобщенных скоростей
и обобщенных ускорений 
,
:
=
=
+
.
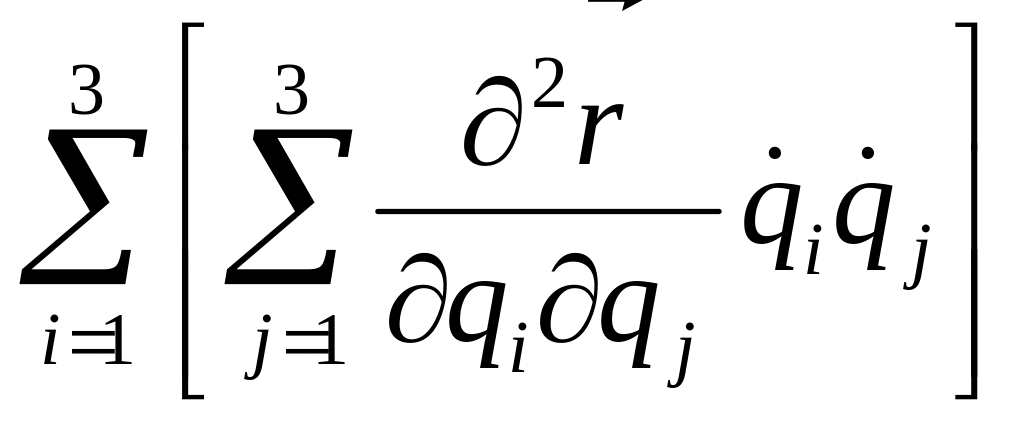В проекциях на абсолютные оси , , оно примет вид:
=
=
+
, 
=
=
+
,
=
=
+
.
Запишем теперь разложение ускорения по базису , , основной системы с началом в точке и по базису , , ДПСК:
=
=
+
+
.
(37)
Умножая обе части равенства последовательно на , , скалярно, находим:
=
(
,
(
,
(
,
,
=
(
,
(
,
(
,
,
=
(
,
(
,
(
,
.
В матричном представлении данные соотношения примут вид:
=
,
или
=
.
Они
дают связь контравариантных
координат
,
,
ускорения
с его декартовыми координатами
,
,
.
Из равенства
подстановкой в него разложения (37)
получаем формулу для
:
=
,
где
— модуль ускорения
.
Построим
теперь формулу Лагранжа для вычисления
ковариантных координат
,
,
ускорения
.
Согласно определению ковариантных
координат можем записать
=
,
.
Подставим в правую часть этого равенства
значение орта
,
вычисленное в точке
,
=
и вынесем за знак скалярного произведения. В результате придем к следующему выражению для :
=
(
,
.
В
нем, в соответствии с определением
понятия ускорения точки, производная
вычисляется вдоль движения
=
,
=
,
=
.
Поэтому в множителе
производная по времени строится от
суперпозиции функций
и
,
,
.
А
потому, согласно свойству б) функции
из леммы
Лагранжа, множитель
можно заменить производной
.
Кроме того, по свойству а) из
той же леммы,
множитель
можно заменить производной
.
А тогда выражение для
примет вид
=
.
(38)
Введем
функцию
,
где
задается формулой (31).
Будем иметь
,
.
Подставляя в (38), окончательно найдем
=
,
.
(39)
Эта формула называется формулой Лагранжа для вычисления ковариантных координат ускорения точки. Таким образом, доказали следующую теорему.
Теорема Лагранжа.
Ковариантные координаты вектора ускорения материальной точки выражаются по формуле (39).
Если
криволинейные координаты ортогональны,
то
=
,
.
В таком случае формула (38) позволяет
вычислить контравариантные координаты
вектора
.
Примечание 2.
Оператор
=
называется оператором
Эйлера-Лагранжа.
Через него формула Лагранжа записывается
следующим образом
=
,
где
.
§6. Кинематические характеристики точки в цилиндрических координатах.
Определим кинематические характеристики точки в цилиндрических координатах. Как отметили в §5, связь цилиндрических и декартовых координат задается формулами
=
,
=
,
=
,
=
. (1)
Полагаем = , = , = .
1. Вычислим базис криволинейных координат в произвольной точке
= , .
Для этого находим коэффициенты Ламе:
=
=
.
Подставляя
формулы (1) для
,
,
и вычисляя производные по
,
получим
.
Аналогично
вычисляются
, 
:
=
=
,
=
=1.
А тогда
=
=
+
=
,
=
=-
+
=
=
,
=
=
=
.
Направления векторов , , показаны на рис.1 §5.
2.
Непосредственным вычислением
и (
,
)
для
легко показать, что
,
,
— ортонормированный ортогональный
базис, т.е. цилиндрическая система
координат — это ортогональная
криволинейная система координат.
3. Вычислим скорость в проекциях на орты , , . Поскольку цилиндрическая система координат ортогональная, то
=
=
,
=
=
,
=
=
.
А
тогда, поскольку
=
,
получаем
=
=
=
,
=
=
=
,
=
=
=
,
=
=
,
=
.
Из последней формулы легко находятся направляющие косинусы в декартовой системе координат :
=
, 
=
,
=
.
4. Вычислим ускорение в проекциях на орты , , . Применим формулу Лагранжа. Для этого определим функцию :
=
.
Отсюда
находим
=
,
=
.
Согласно формуле Лагранжа имеем
=
=
=
-
.
Следовательно,
=
-
.
Проведя аналогичные расчеты для координат и , получим:
=
,
,
=
=
=
-
=
(
),
или
=
,
=
,
,
=
=
=
-
,
или
=
.
Тогда
для
будем иметь
=
.
Направляющие косинусы в системе будут выражаться по формулам:
=
(
-
),
=
(
+
),
=
.
Формулы для направляющих косинусов вектора и вектора получены проектированием на орты , , векторов
=
+
+
; 
=
+
+
.