
- •§5. Задание движения материальной точки в криволинейных координатах.
- •1º. Понятие криволинейных (обобщенных) координат точки.
- •2º. Задание движения материальной точки в криволинейных координатах.
- •3º. Геометрические характеристики криволинейных координат.
- •4º. Коэффициенты Ламе. Основная система координат.
- •5º. Ортогональные криволинейные координаты и условия их ортогональности.
- •6º. Линейные перемещения точки и их связь с линейными перемещениями в криволинейных координатах.
- •7º. Союзная система координат и ее связь с основной.
- •8º. Скорость точки в криволинейной системе координат.
- •9º. Ускорение точки в криволинейных координатах.
- •§6. Кинематические характеристики точки в цилиндрических координатах.
- •§7. Кинематические характеристики точки в сферических координатах.
7º. Союзная система координат и ее связь с основной.
Ковариантные координаты вектора.
Пусть
![]() — произвольный вектор;
,
,
— базис основной системы координат;
— произвольный вектор;
,
,
— базис основной системы координат;
![]() ,
— матрица метрических коэффициентов
этой системы,
,
— матрица метрических коэффициентов
этой системы,
![]() ;
;
![]() ,
, ![]() ,
, ![]() — координаты
вектора
в основной системе. Как отмечено выше,
они называются контравариантными
координатами вектора
.
Введем следующее понятие.
— координаты
вектора
в основной системе. Как отмечено выше,
они называются контравариантными
координатами вектора
.
Введем следующее понятие.
Определение 8.
Ковариантными
координатами
вектора
называются величины
![]() ,
определяемые по формуле:
,
определяемые по формуле:
![]() ,
.
,
.
Геометрический смысл ковариантных координат вектора следующий:
если вектора , , являются ортами, то — это ортогональные проекции вектора на координатные оси основной системы координат,
если вектора , , не являются ортами, то — это ортогональные проекции вектора на указанные оси, умноженные на
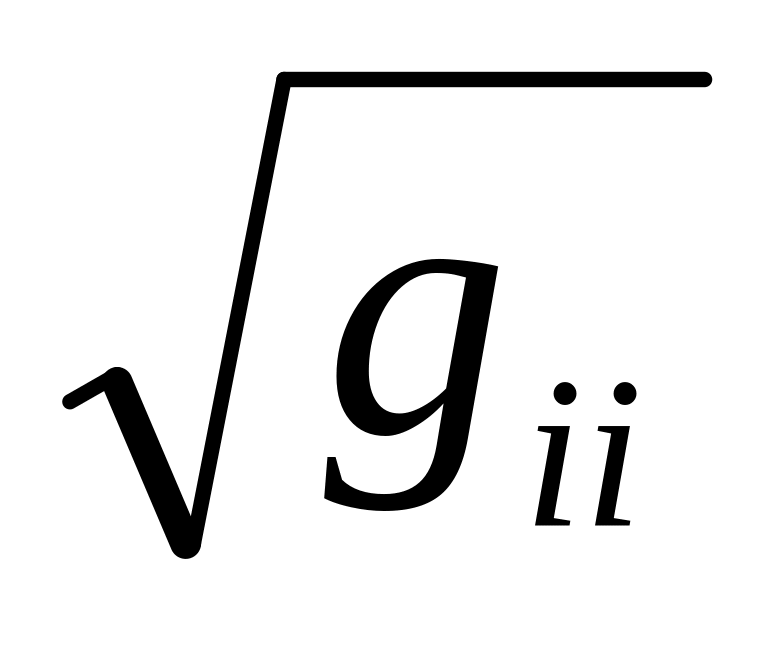 ,
где
,
где
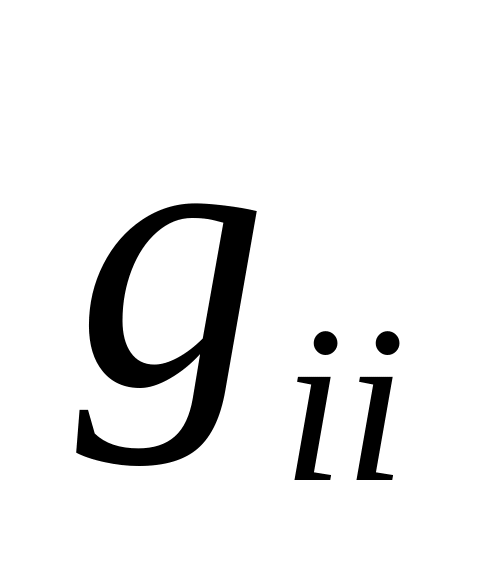
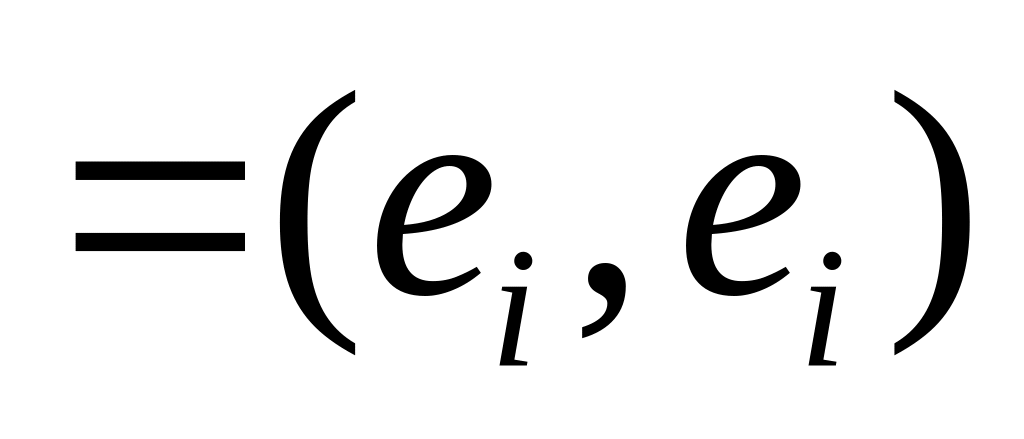 =
=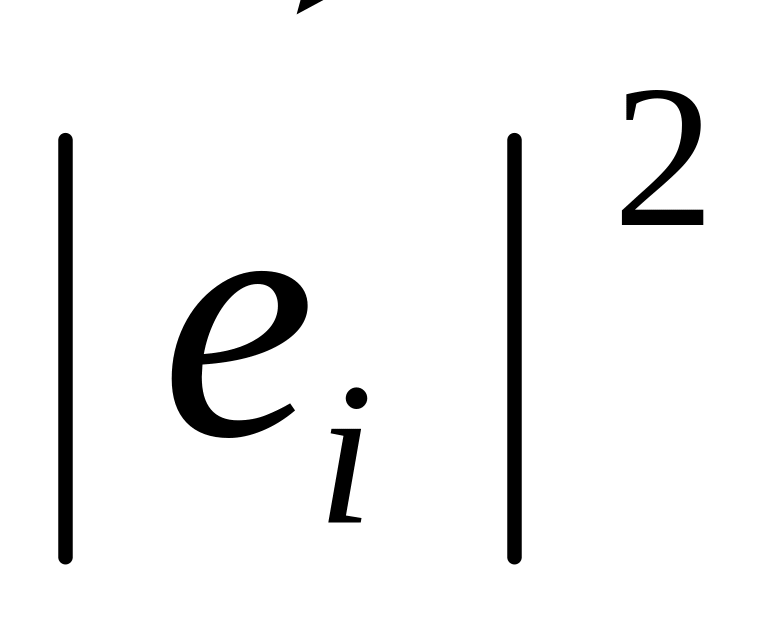 .
.
Введем
следующие три вектора
![]() ,
, ![]() ,
, ![]() :
:
![]() (
(
![]() ),
(
),
(
)
(15)
),
(
),
(
)
(15)
и
изучим их свойства. В
(15) буквой
![]() обозначена величина смешанного
произведения векторов
,
,
:
обозначена величина смешанного
произведения векторов
,
,
:
![]() .
(16)
.
(16)
Как
показано в п.5º,
в этих обозначениях будем иметь
![]() .
.
Свойство 1.
Справедлива формула
![]()
![]() (17)
(17)
для всех .
Докажем
утверждение для
=1.
При
![]() =1
в силу (16) имеем:
=1
в силу (16) имеем:
(
,
)
(
,
)
(
,
,
)![]() .
.
При =2,3 можем записать
(
,![]() )
(
,
,
)
.
)
(
,
,
)
.
Данное
равенство выполняется, поскольку в нем
=
либо
=
,
а смешанные произведения
![]() и
и
![]() равны нулю. Для
равны нулю. Для
![]() справедливость свойства 2
доказывается
аналогично.
справедливость свойства 2
доказывается
аналогично.
Свойство 2.
Векторы , , линейно независимы, и для смешанного произведения этих векторов справедлива формула
( , , ) . (18)
Для доказательства утверждения вычислим сначала векторное произведение векторов и :
=
![]() (
)
(
)
![]() .
.
В данной записи воспользовались третьей формулой в соотношениях (15) и формулой двойного векторного произведения.
Согласно
(17) имеем
![]() и
и
![]() .
Поэтому
окончательно находим
.
Поэтому
окончательно находим
. (19)
Подставляя (19)
в смешанное произведение векторов
,
,
и учитывая (17) для
![]() ,
получим
,
получим
![]()
![]() .
.
Что и требовалось доказать.
Введем косоугольную аффинную систему координат с полюсом в точке и базисными векторами, совпадающими с , , .
Эта система координат называется союзной по отношению к исходной, т.е. основной, системе координат с базисом , , и полюсом в точке .
Матрицу
метрических коэффициентов союзной
системы будем обозначать
![]() ,
а элементы этой матрицы —
,
а элементы этой матрицы —
![]() ,
.
Так что будем иметь:
,
.
Так что будем иметь:
![]() ,
,
=
,
,
=![]() .
.
Пусть
![]() ,
, ![]() ,
, ![]() — координаты
вектора
в союзной
системе
координат, и
— координаты
вектора
в союзной
системе
координат, и
![]() ,
, ![]() ,
, ![]() — координаты
этого вектора в
основной
системе
координат,
т.е. его контравариантные координаты.
— координаты
этого вектора в
основной
системе
координат,
т.е. его контравариантные координаты.
Покажем, что координаты вектора в союзной системе совпадают с его ковариантными координатами, т.е. справедлива формула
![]() =
=![]() ,
.
(20)
,
.
(20)
Действительно, по определению координат вектора в союзной системе можем записать
=![]() .
.
Умножая это равенство скалярно на , слева (по определению ковариантных координат вектора ) будем иметь
![]() ,
,
где — -я ковариантная координата вектора .
Учитывая (17), справа получим
![]() .
.
Таким образом, равенства (20) доказаны.
Установим
связь между матрицами
и
![]() .
А именно, докажем
справедливость
соотношения
.
А именно, докажем
справедливость
соотношения
=![]() .
(21)
.
(21)
Действительно, для любого вектора можем записать
=![]() =
=![]() .
(22)
.
(22)
Умножая (22) последовательно (для ) скалярно на , получим
=![]() ,
.
,
.
Эта система в матричном представлении имеет вид:
![]()
![]()
![]() .
(23)
.
(23)
Умножая
(22) последовательно (для
)
скалярно на
![]() ,
находим
,
находим
![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]() ,
.
,
.
Соответственно, в матричном представлении:
= .
Подставляя в левую часть соотношение (23), придем к системе
![]() ,
,
где
![]() — единичная матрица размерности
— единичная матрица размерности
![]() .
В силу произвольности вектора
получаем
.
В силу произвольности вектора
получаем
![]() .
.
Отсюда следует справедливость соотношения (21).
Докажем следующее утверждение.
Если по заданной исходной основной системе координат построить союзную систему, а затем построенную союзную систему взять в качестве новой основной и построить союзную к ней систему, то эта последняя союзная система будет совпадать с исходной основной системой координат.
Коротко это утверждение формулируется так:
«Союзная система к союзной совпадает с основной».
Утверждение будет доказано, если покажем, что
![]() =
=![]() (
)
(
)![]() ,
,
![]() =
=![]() (
)
(
)![]() ,
,
![]() =
(
)
=
(
)![]() ,
,
где
![]() .
.
Докажем, например, справедливость первой формулы (остальные — доказываются аналогично).
Выше
было установлено (см. (19))
.
Кроме того, из (18) (свойство 2)
имеем
![]() .
Поэтому для
можем записать
.
Поэтому для
можем записать
=
(
)![]() =
,
=
,
что и требовалось доказать.
Из доказанных свойств, в частности, вытекает, что если основной базис является ортонормированным ортогональным базисом, то союзная система координат совпадает с основной. В этом случае ковариантные координаты вектора (величины ) совпадают с соответствующими контравариантными координатами (величинами ).
Примечание 1.
Поясним смысл терминов «ковариантные» и «контравариантные» координаты.
Выше доказали формулу (23):
,
где , , — координаты вектора в союзной системе, , , — координаты этого же вектора в основной системе, — матрица метрических коэффициентов основной системы.
Из (23) заключаем, что имеет второй смысл. Она является матрицей перехода от основной к союзной системе координат.
Заметим, что основное правило, по которому осуществляется расчет координат вектора в любой новой системе координат по координатам этого вектора, известным в некоторой фиксированной аффинной системе, является соотношение вида
![]()
![]() ,
(24)
,
(24)
где ![]() — координаты
вектора
в «новой системе»
координат,
,
,
— координаты
вектора
в заданной
(фиксированной,
«старой»)
системе,
— неособая матрица, называемая матрицей
перехода от «старой» системы
к «новой»
системе
координат.
— координаты
вектора
в «новой системе»
координат,
,
,
— координаты
вектора
в заданной
(фиксированной,
«старой»)
системе,
— неособая матрица, называемая матрицей
перехода от «старой» системы
к «новой»
системе
координат.
Фиксируем
неособую матрицу
.
Будем говорить,
что координаты
![]() любого вектора
согласованно
изменяются по отношению к его координатам
,
,
заданным в фиксированной
основной
системе
координат, если они рассчитываются по
формуле (24).
любого вектора
согласованно
изменяются по отношению к его координатам
,
,
заданным в фиксированной
основной
системе
координат, если они рассчитываются по
формуле (24).
Определение 9.
Система координат, для которой является матрицей перехода от фиксированной основной системы, называется согласованной с основной системой через матрицу .
Из (23) следует, что союзная система является согласованной с основной через матрицу метрических коэффициентов основной системы. Поэтому координаты векторов в этой (союзной) системе называются ковариантными (слово «ковариантные» в переводе с французского означает «согласованно изменяющиеся»). Они согласованно изменяются через матрицу .
Основные координаты вектора могут быть вычислены через согласованные координаты (координаты этого вектора в новой системе координат) при фиксированной матрице по формуле
![]() ,
(25)
,
(25)
Очевидно,
матрица
![]() является
матрицей перехода от «новой»
системы
координат к
«старой»
(основной)
системе.
является
матрицей перехода от «новой»
системы
координат к
«старой»
(основной)
системе.
В этом случае выражение (25) можем трактовать как обратный закон пересчета координат, а координаты вектора в основной («старой») системе могут рассматриваться как координаты «противоположно меняющиеся» при фиксированной матрице по отношению к новым координатам.
Поэтому координаты вектора в основной системе (координаты ) по отношению к союзной системе принято называть контравариантными координатами (при переводе с французского слово «контравариантные» означает «обратно изменяющиеся»).
Термин «контравариантные координаты» имеет и другой смысл. А именно, он означает, что эти координаты меняются (рассчитываются) по обратному закону относительно некоторой фиксированной системы координат. Если матрица задана, то согласно определению 9 эти координаты согласованы с заданной фиксированной системой координат через обратную матрицу .
Применим это правило к основной и союзной системам координат.
Если
считать, что координаты союзной системы
фиксированы (заданы), а основной
— пересчитываются по ним, то этот
пересчет осуществляется с помощью
обратной матрицы
![]() .
А тогда согласно указанному выше правилу
координаты
основной системы
следует называть «контравариантными»,
поскольку они согласованы с фиксированными
(союзными) через обратную матрицу
.
.
А тогда согласно указанному выше правилу
координаты
основной системы
следует называть «контравариантными»,
поскольку они согласованы с фиксированными
(союзными) через обратную матрицу
.
