2º. Задание движения материальной точки в криволинейных координатах.

Определение 2.

Движением материальной точки в криволинейных координатах называем дважды непрерывно дифференцируемые функции ,  ,  , задающие криволинейные координаты точки в каждый момент времени , где они определены.

Задать движение в криволинейных координатах — это значит:

• задать зависимость положения материальной точки  от ее криволинейных координат = ,

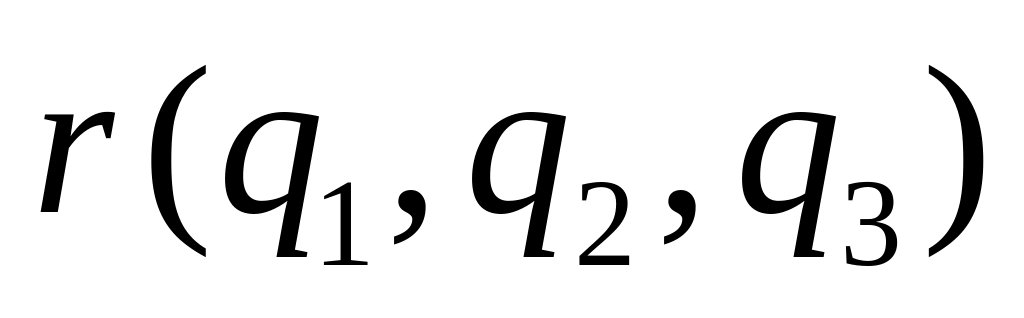• задать закон изменения криволинейных координат материальной точки от времени = , = , = .

Если известно движение  , , материальной точки в криволинейных координатах , то векторное задание ее движения получим подстановкой функций , , в вектор-функцию  , устанавливающую связь положения точки с криволинейными координатами:

.

3º. Геометрические характеристики криволинейных координат.

Пусть соотношение (1)

задает связь криволинейных координат ,  ,  вектора с декартовыми ,  ,  .

Зафиксируем одну из криволинейных координат. Например, положим в (1) = = . В полученном соотношении

= (4)

координаты ,  будем рассматривать как переменные параметры.

Очевидно, в пространстве  уравнение (4) задает поверхность. Она называется координатной поверхностью, отвечающей координате , или первой координатной поверхностью. Обозначим ее .

Аналогично определяются координатные поверхности, отвечающие координате  и координате –  вторая и третья координатные поверхности.

Обозначим их и , соответственно. Уравнения поверхностей и получаются из (1) фиксированием одной из координат = или = , соответственно.

Если зафиксируем в (1) значения двух криволинейных координат = = и = = , то будем иметь

= .

Это соотношение задает в пространстве кривую, которая является пересечением координатных поверхностей и :

= , = .

Такая кривая называется первой координатной линией. Аналогично определяются вторая и третья координатные линии. Их уравнения имеют вид и , соответственно. Вторая координатная линия является пересечением координатных поверхностей и :

и ,

а третья координатная линия — пересечением поверхностей и :

и .

Координатные линии, очевидно, пересекаются в точке  , обобщенные координаты которой имеют значения ,  ,  . Здесь ,  ,  — значения переменных ,  ,  , по которым строились первая, вторая и третья координатные линии.

Вернемся к примеру 1. В цилиндрической системе координатные поверхности и координатные линии изображены на рис. 1.

Координатными поверхностями являются:

• первая – = 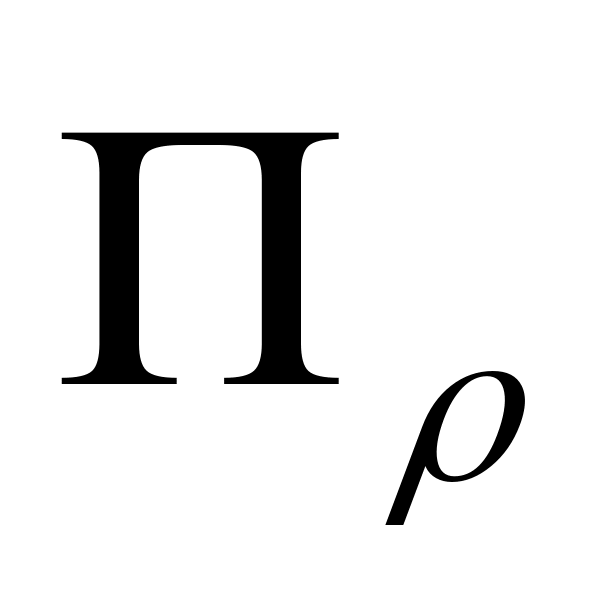– цилиндрическая поверхность (на рисунке изображена часть этой поверхности, ограниченная дугами и 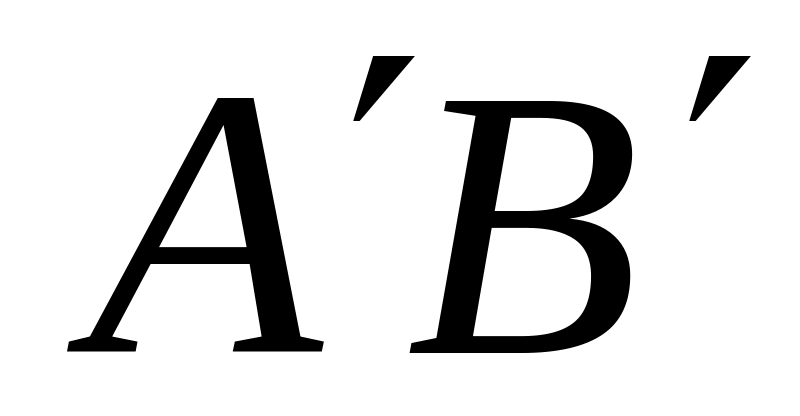и отрезкам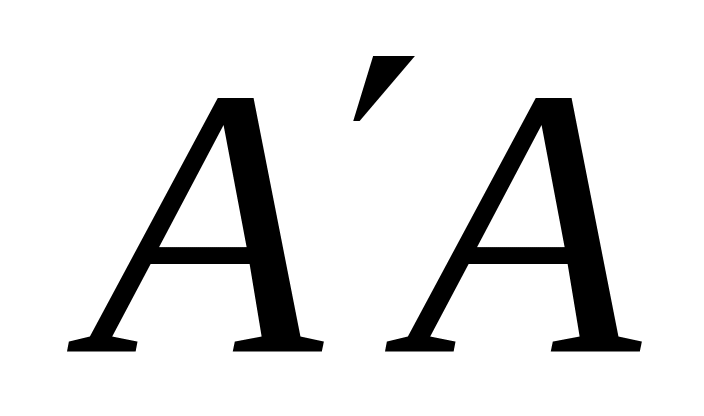и и );

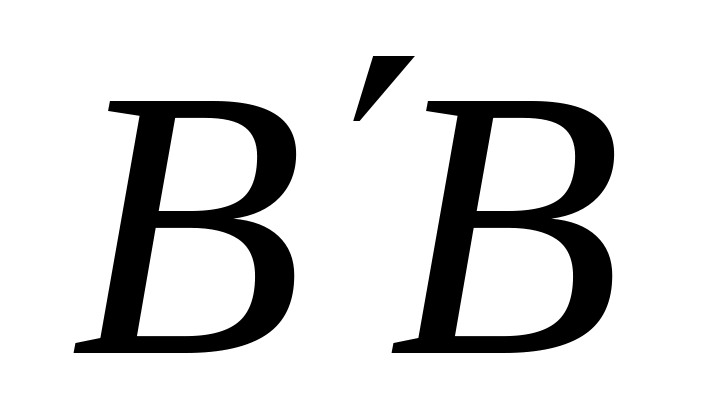• вторая – = – полуплоскость, ограниченная осью  и проходящая через ось  и точку  (на рисунке – это плоскость прямоугольника );

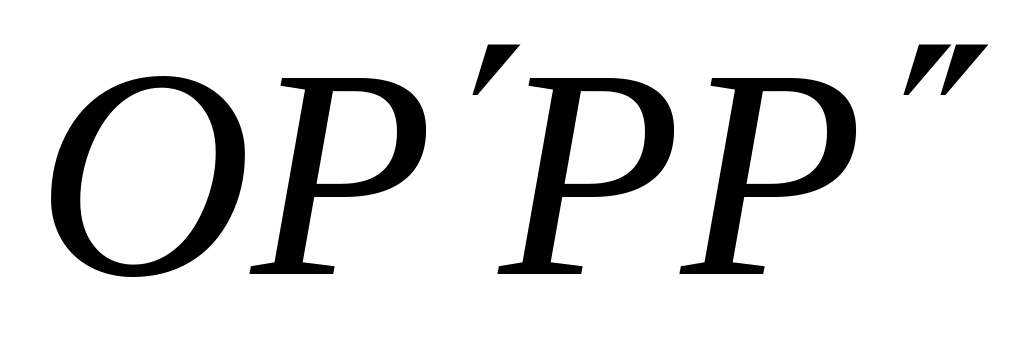• третья – = 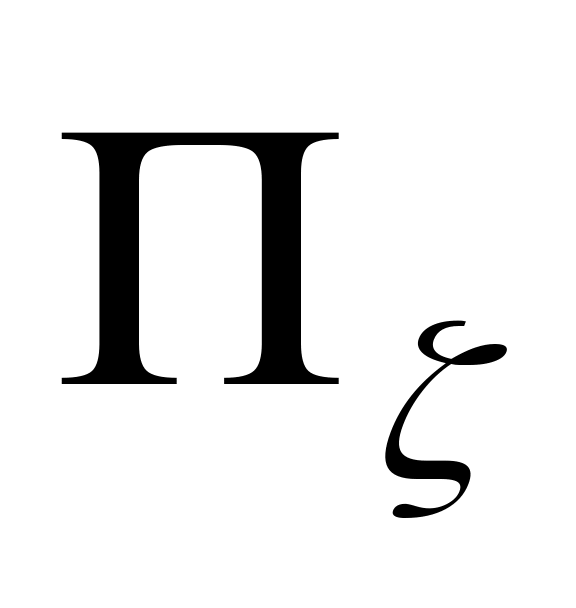– плоскость, параллельная плоскости и проходящая через точку  (на рисунке – это плоскость сектора  ).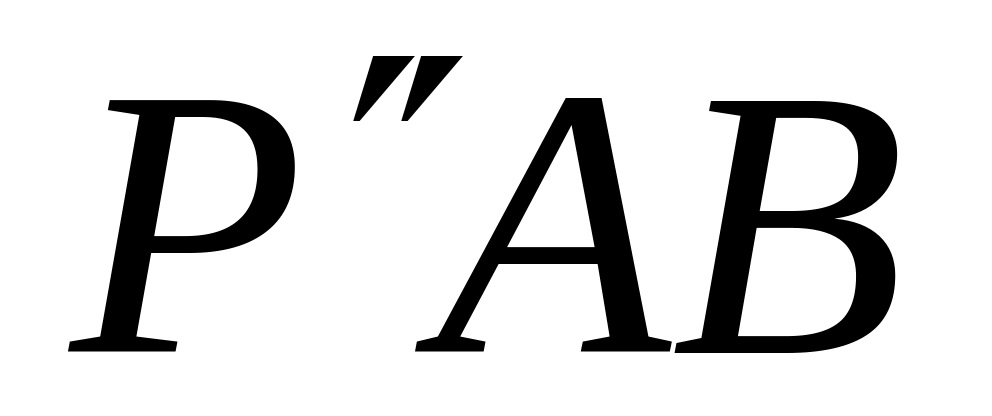

Координатные линии:

• ( )=( ) – первая (луч 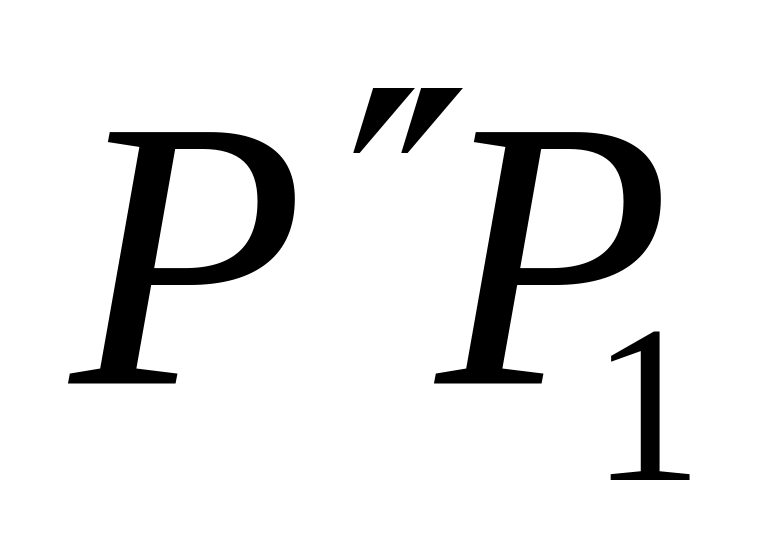с направляющим ортом );

• ( )=( ) - вторая (окружность радиуса с центром в точке 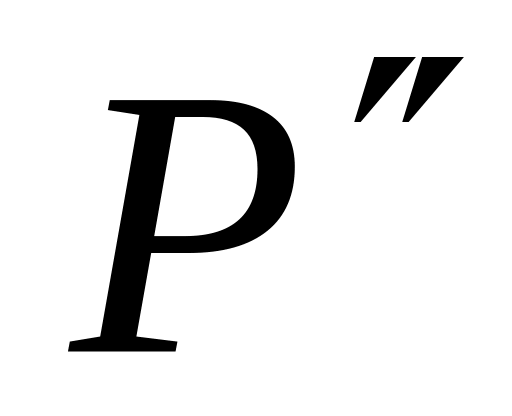 ; ее плоскость ортогональна орту ; – орт касательной в точке  );

• ( )=( ) – третья (прямая 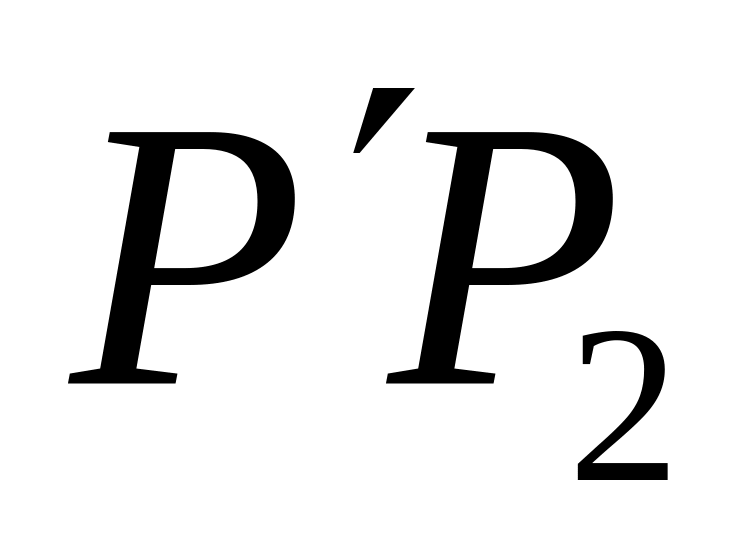с направляющим ортом = ).