Раздел 2 аналитическая статистика

Глава 5. Показатели вариации

5.1. Основные понятия

Исследование вариации в статистике и социально-экономических исследованиях имеет важное значение, так как величина вариации признака в статистической совокупности характеризует ее однородность. Вариация – колебание, многообразие, изменяемость величины признака у отдельных единиц совокупности.

В статистической практике для изучения и измерения вариации используют различные показатели (меры) вариации в зависимости от поставленных задач. Так, к абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия. Относительные показатели вариации - это коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Размах вариации (R) является наиболее простым измерителем вариации признака. Он определяется как разность между наибольшим и наименьшим значениями варьирующего признака.

где - наибольшее и наименьшее значение варьирующего признака.

Среднее линейное отклонение () представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения:

- невзвешенное среднее линейное

отклонение;

- взвешенное среднее линейное

отклонение.

Символы и имеют то же значение, что и в предыдущей главе. Рассмотренные выше показатели имеют ту же размерность, что и признак, для которого они вычисляются.

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений от их средней величины (обозначается греческой буквой - «сигма квадрат»). Дисперсия вычисляется по формулам простой невзвешенной и взвешенной:

- невзвешенная;

- взвешенная.

Как и любая средняя, дисперсия имеет определенные математические свойства:

а) если все значения признака уменьшить (увеличить) на определенную величину, дисперсия не изменится;

б) если все значения признака изменить в К раз, то дисперсия изменится в К² раз;

в) в случае замены частот долями дисперсия не изменится.

Среднее квадратическое отклонение представляет собой корень квадратный из среднего квадрата отклонений отдельных значений признака от их средней:

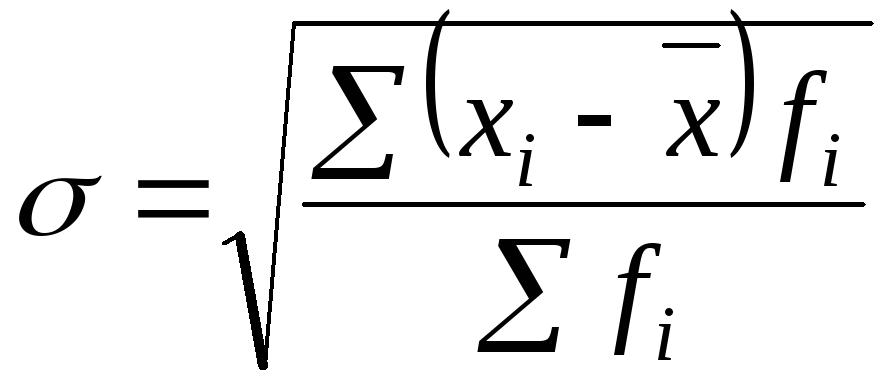- невзвешенное;

- взвешенное.

Среднее квадратическое отклонение – величина именованная, имеет размерность осредняемого признака.

Расчет дисперсии прямым способом в ряде случаев трудоемок. Упростить ее вычисления можно, используя расчет дисперсии по способу отсчета от условного нуля или способу моментов по следующей формуле:

.

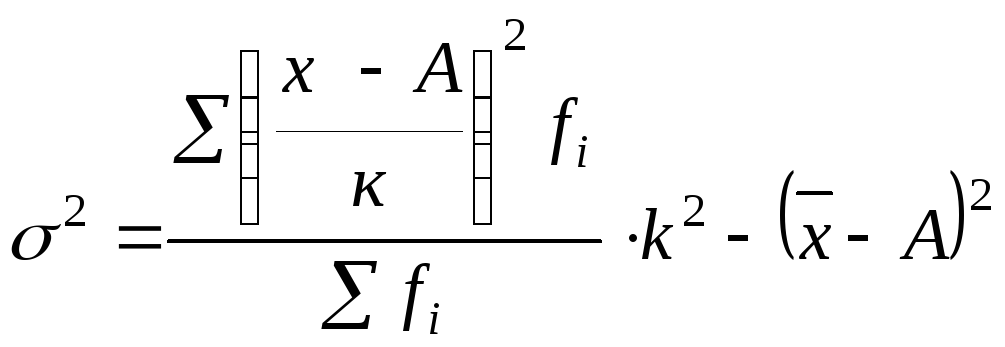Формула расчета дисперсии по способу моментов имеет следующий вид:

,

где k – величина интервала;

А – условный нуль, в качестве которого используют середину

интервала с наибольшей частотой;

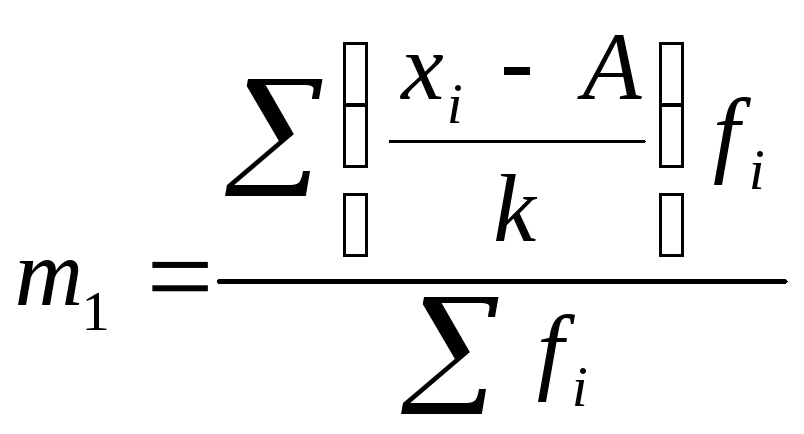- начальный момент первого порядка;

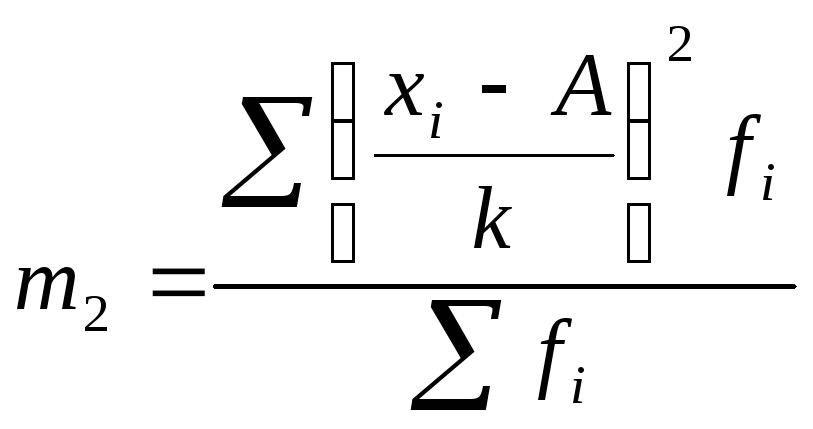- начальный момент второго порядка.

В случае, когда А приравнивается к нулю и, следовательно, не вычисляются отклонения, формула принимает вид:

или

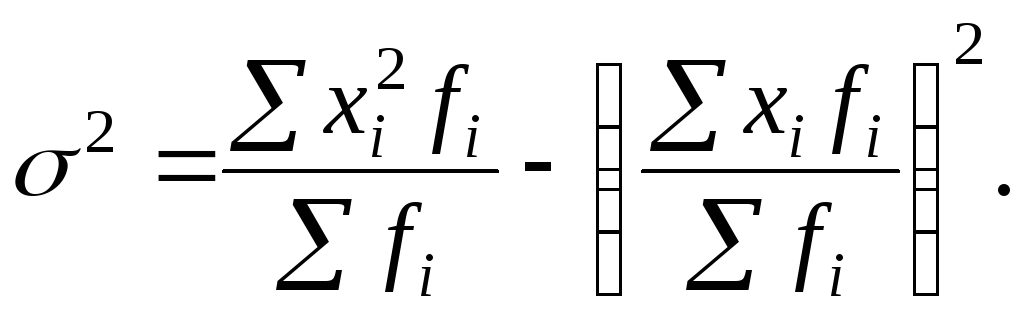
Для целей сравнения колебания различных признаков в одной и той же совокупности или же при сравнении колебаний одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха, или среднего линейного отклонения, или среднего квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 %. Различают следующие относительные показатели вариации:

• коэффициент осцилляции – процентное отношение размаха вариации к средней величине признака:

%,

• линейный коэффициент вариации – процентное отношение среднего линейного отклонения к средней величине признака:

%,

• коэффициент вариации – процентное отношение среднего квадратического отклонения к средней величине признака:

%.

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

Правило сложения дисперсий. Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповую.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:

.

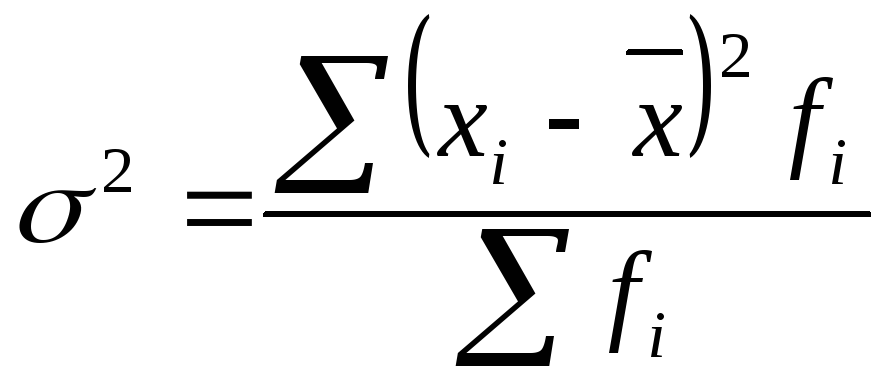Межгрупповая дисперсия характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под действием признака – фактора, положенного в основание группировки. Она рассчитывается по формуле:

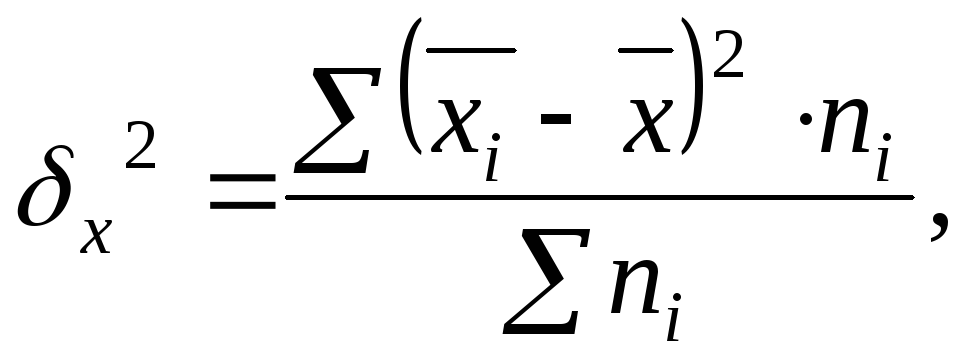
где - соответственно средние и численности по отдельным группам.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака - фактора, положенного в основание группировки. Она исчисляется следующим образом:

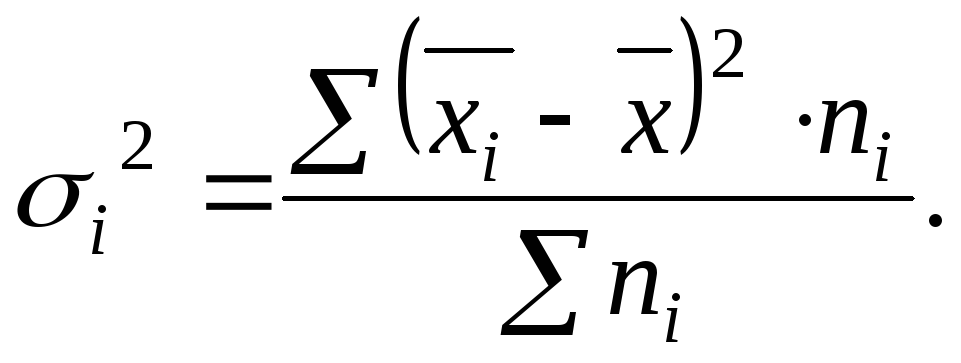
Средняя из внутригрупповых дисперсий:

Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу, общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.

В качестве статистических характеристик вариационных рядов распределения рассчитываются так называемые структурные средние – мода и медиана.

Мода – значение признака, наиболее часто встречающее в исследуемой совокупности.

Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.

Для интервальных вариационных рядов мода определяется по формуле:

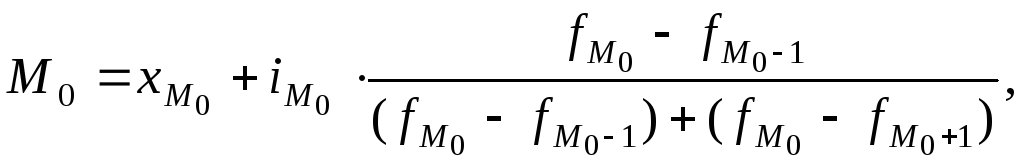
где - нижняя граница значения интервала, содержащего моду;

- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным.

Медиана интервального ряда распределения определяется по формуле:

где - нижняя граница значения интервала, содержащего медиану;

- величина медианного интервала;

- сумма частот;

- сумма накопленных частот, предшествующих медианному

интервалу;

- частота медианного интервала.