
- •Основные понятия
- •Скалярное поле
- •Предел функции нескольких переменных
- •Дифференцирование функций нескольких переменных Частные производные
- •Условия дифференцируемости
- •Производная по направлению
- •Дифференцирование сложной функции
- •Инвариантность формы полного дифференциала
- •Нормаль и касательная плоскость к поверхности
- •Геометрический смысл полного дифференциала функции двух переменных
- •Производная функции, заданной неявно
- •Производные и дифференциалы высших порядков
- •Частные производные высших порядков
- •Дифференциалы высших порядков
- •Операторная форма дифференциалов высших порядков
- •Формула Тейлора
- •Экстремумы функций нескольких переменных Точки максимума и минимума
- •Необходимое условие экстремума
- •Достаточные условия экстремума
- •Условный экстремум
- •Методы нахождения условного экстремума Метод исключения переменных
- •Метод неопределенных множителей Лагранжа
- •Геометрический смысл условного экстремума функции:
- •Наибольшие и наименьшие значения
- •Составители
- •Функции нескольких переменных Методические указания к самостоятельному изучению соответствующего раздела курса математики для студентов всех специальностей
Формула Тейлора
Пусть
функция
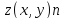 раз
дифференцируема в некоторой окрестности
точки
раз
дифференцируема в некоторой окрестности
точки
 .
.
Формула
Тейлора
 –го
порядка для функции
–го
порядка для функции
 имеет вид
имеет вид
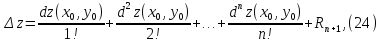
где
 — некоторая функция
— некоторая функция
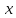 и
и
 ,
называемая остаточным членом.
,
называемая остаточным членом.
Известно, что
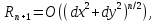
( форма Пеано остаточного члена формулы Тейлора) и
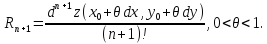
( форма Лагранжа остаточного члена формулы Тейлора).
Формула Тейлора в виде (24) легко распространяется на функции с любым числом аргументов.
Экстремумы функций нескольких переменных Точки максимума и минимума
Пусть
функция нескольких переменных
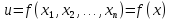 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
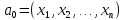 .
.
Точка
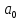 называется точкой
локального максимума (локального
минимума)
функции
называется точкой
локального максимума (локального
минимума)
функции
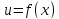 , если существует такая окрестность
, если существует такая окрестность
 точки
точки
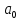 , что для всех точек
, что для всех точек
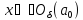 выполняется неравенство
выполняется неравенство
 .
.
Значение
функции
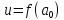 в этой точке называется локальным
максимумом (или локальным минимумом)
функции
и обозначается
в этой точке называется локальным
максимумом (или локальным минимумом)
функции
и обозначается
 (или
(или
 ).
).
Если
при
 имеет место неравенство
имеет место неравенство
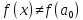 , то точка
, то точка
 называется точкой строгого
локального максимума (минимума).
называется точкой строгого
локального максимума (минимума).
Точки максимума и минимума функции называются точками экстремума, а максимумы и минимумы — экстремумами функции.
Необходимое условие экстремума
(
Необходимое условие экстремума)
Теорема:
Если функция нескольких переменных
 имеет экстремум в некоторой точке, то
в этой точке каждая ее частная производная
равна нулю или не существует.
имеет экстремум в некоторой точке, то
в этой точке каждая ее частная производная
равна нулю или не существует.
Внутренние точки из области определения функции, в которых выполняются необходимые условия экстремума, называются критическими. Если в критической точке функция дифференцируема, то такая точка называется стационарной.
В
стационарной точке
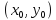 функции
функции
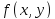 существуют частные производные
существуют частные производные
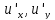 и
и

Достаточные условия экстремума
Пусть
функция
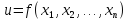 имеет непрерывные частные производные
до 2–го порядка включительно в некоторой
окрестности ее стационарной
точки
имеет непрерывные частные производные
до 2–го порядка включительно в некоторой
окрестности ее стационарной
точки
 .
.
Пусть
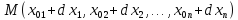 —
некоторая точка из этой окрестности.
Тогда
—
некоторая точка из этой окрестности.
Тогда
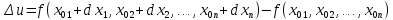
— приращение
функции, которое она получает при
смещении из точки
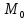 в точку
в точку
 .
.
По формуле Тейлора имеем

где
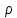 — расстояние между точками
— расстояние между точками
 и
и
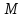 .
.
Так
как
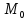 — стационарная точка функции
— стационарная точка функции
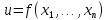 , то
, то
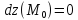 .
.
Допустим,
что
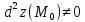 для всех точек
для всех точек
 из некоторой окрестности
из некоторой окрестности
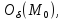 достаточно малой, чтобы в ней выполнялось
неравенство
достаточно малой, чтобы в ней выполнялось
неравенство
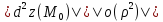 . Тогда знаки
. Тогда знаки
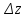 и
и
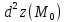 одинаковы.
одинаковы.
Если
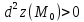 для всех точек
для всех точек
 из окрестности
из окрестности
 ,
то и
,
то и
 .
В
этом случае функция
.
В
этом случае функция
 имеет минимум в точке
имеет минимум в точке
 .
.
Если
 для всех точек
для всех точек
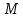 из окрестности
из окрестности
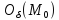 , то и
, то и
 .
В
этом случае функция
.
В
этом случае функция
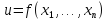 имеет
максимум в точке
имеет
максимум в точке
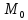 .
.
Таким образом, достаточным условием экстремума функции нескольких переменных в ее стационарной точке является знакоопределенность (положительная или отрицательная определенность) дифференциала 2–го порядка в этой точке.
Достаточные условия экстремума функции 2–х переменных
Теорема.
Пусть функция
 определена и имеет непрерывные частные
производные второго порядка в стационарной
точке
определена и имеет непрерывные частные
производные второго порядка в стационарной
точке
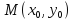 (т.е.
(т.е.
 ):
):
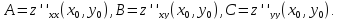
Тогда:
-
если
 , то
, то
 — точка экстремума, причем при
— точка экстремума, причем при
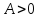 — точка минимума, при
— точка минимума, при
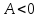 — точка максимума;
— точка максимума;
-
если
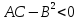 , то
, то
 не является точкой экстремума;
не является точкой экстремума;
-
если
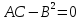 , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
Доказательство приведено на стр. 163 [1]
Пример:
Найти точки экстремума функции
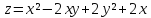 .
.
Для поиска стационарных точек решим систему
 .
.
Итак,
стационарная точка
 .
При этом
.
При этом
 .
Тогда
.
Тогда
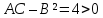 ,
следовательно, в стационарной точке
достигается экстремум, а именно минимум
(так как
,
следовательно, в стационарной точке
достигается экстремум, а именно минимум
(так как
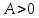 ).
).
