
- •Основные понятия
- •Скалярное поле
- •Предел функции нескольких переменных
- •Дифференцирование функций нескольких переменных Частные производные
- •Условия дифференцируемости
- •Производная по направлению
- •Дифференцирование сложной функции
- •Инвариантность формы полного дифференциала
- •Нормаль и касательная плоскость к поверхности
- •Геометрический смысл полного дифференциала функции двух переменных
- •Производная функции, заданной неявно
- •Производные и дифференциалы высших порядков
- •Частные производные высших порядков
- •Дифференциалы высших порядков
- •Операторная форма дифференциалов высших порядков
- •Формула Тейлора
- •Экстремумы функций нескольких переменных Точки максимума и минимума
- •Необходимое условие экстремума
- •Достаточные условия экстремума
- •Условный экстремум
- •Методы нахождения условного экстремума Метод исключения переменных
- •Метод неопределенных множителей Лагранжа
- •Геометрический смысл условного экстремума функции:
- •Наибольшие и наименьшие значения
- •Составители
- •Функции нескольких переменных Методические указания к самостоятельному изучению соответствующего раздела курса математики для студентов всех специальностей
Производные и дифференциалы высших порядков
При изучении этой темы вы познакомитесь с понятиями и свойствами частных производных и дифференциалов высших порядков, научитесь их вычислять. Познакомитесь также с формулой Тейлора, важной для дальнейших приложений.
Частные производные высших порядков
Пусть
функция
 в некоторой окрестности точки
в некоторой окрестности точки
 имеет частные производные
имеет частные производные

или в других обозначениях
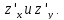
Частные
производные являются функциями
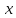 и
и
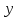 ,
которые, в свою очередь, могут иметь
частные производные
,
которые, в свою очередь, могут иметь
частные производные
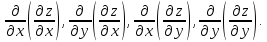
Если
это так, то последние называются частными
производными 2–го порядка
функции
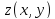 и обозначаются соответственно:
и обозначаются соответственно:
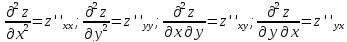
Аналогично определяются частные производные более высоких порядков.
Частные
производные, образованные дифференцированием
по различным аргументам, называются
смешанными
частными производными.
Например, смешанные производные 2–го
порядка функции двух переменных суть
 и
и
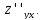
Среди смешанных производных одного порядка выделяют производные:
-
отличающиеся количеством дифференцирований по одноименным аргументам (например,
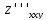 и
и
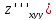 ;
;
-
отличающиеся лишь порядком дифференцирования по аргументам (например,
 ).
).
Теорема о равенстве смешанных частных производных:
Теорема: Если смешанные частные производные, отличающиеся лишь порядком дифференцирования, непрерывны в некоторой точке, то их значения в этой точке равны.
Дифференциалы высших порядков
Пусть
функция
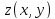 дифференцируема в точке
дифференцируема в точке
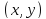 и ее аргументам
и ее аргументам
 и
и
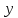 даны
приращения соответственно
даны
приращения соответственно
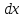 и
и
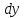 . Тогда полный дифференциал первого–го
порядка функции
. Тогда полный дифференциал первого–го
порядка функции
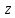 определяется формулой
определяется формулой
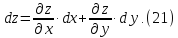
Если
функция
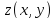 дифференцируема в некоторой окрестности
точки
дифференцируема в некоторой окрестности
точки
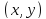 , то
, то
 является функцией
является функцией
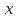 и
и
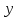 . Кроме того,
. Кроме того,
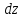 зависит также от
зависит также от
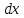 и
и
 .
.
Пусть
 и
и
 — независимые переменные. Приращения
независимых переменных
— независимые переменные. Приращения
независимых переменных
 и
и
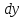 не зависят от
не зависят от
 и
и
 и в этом смысле их можно считать
постоянными. Тогда
и в этом смысле их можно считать
постоянными. Тогда
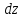 будет функцией только аргументов
будет функцией только аргументов
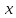 и
и
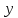 .
Допустим, что эта функция дифференцируема
в точке
.
Допустим, что эта функция дифференцируема
в точке
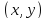 и ее аргументам даны приращения
и ее аргументам даны приращения
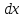 ,
,
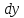 (причем, совпадающие с теми, которые
вызвали приращение функции
(причем, совпадающие с теми, которые
вызвали приращение функции
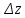 с дифференциалом
с дифференциалом
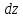 ). Эти приращения вызовут приращение
). Эти приращения вызовут приращение
 , главная линейная часть которого
является полным дифференциалом
, главная линейная часть которого
является полным дифференциалом
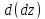 . Этот полный дифференциал называется
дифференциалом
2–го порядка
функции
. Этот полный дифференциал называется
дифференциалом
2–го порядка
функции
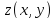 в точке
в точке
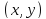 и обозначается символом
и обозначается символом
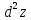 .
.
Покажем,
что дифференциал 2–го порядка выражается
через частные производные 2–го порядка,
вычисленные в точке
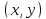 и является квадратичной
функцией (формой)
приращений
и является квадратичной
функцией (формой)
приращений
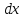 и
и
 .
.
Применяя к (21) правила дифференцирования и учитывая постоянство dx и dy , получаем:
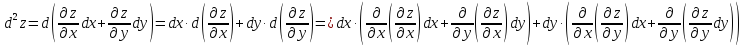
Если
смешанные частные производные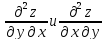
непрерывны
в точке
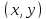 и, следовательно, равны, то
и, следовательно, равны, то
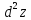 приводится к виду
приводится к виду
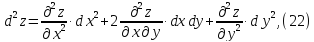
т.е.
является квадратичной формой функции
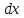 и
и
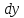 .
.
Операторная форма дифференциалов высших порядков
Если и
и
 рассматривать как обозначения
дифференциальных операторов, результатами
действия которых на функцию
рассматривать как обозначения
дифференциальных операторов, результатами
действия которых на функцию
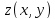 являются частные производные
являются частные производные 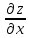 и
и
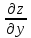 ,
то
,
то
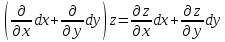
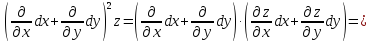
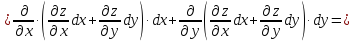
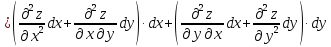
Теперь формулу (22) можно записать в операторной форме
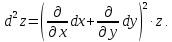
Если
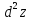 является дифференцируемой функцией
независимых переменных
является дифференцируемой функцией
независимых переменных
 и
и
 в окрестности точки
в окрестности точки
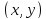 , то аналогично вышеизложенному вводится
понятие дифференциала
3–го порядка:
, то аналогично вышеизложенному вводится
понятие дифференциала
3–го порядка:
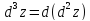 при постоянных
при постоянных
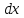 и
и
 .
.
Дифференциал
 –го порядка
определяется как дифференциал от
дифференциала
–го порядка
определяется как дифференциал от
дифференциала
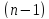 –го порядка:
–го порядка:
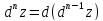 при постоянных
при постоянных
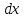 и
и
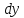 а его связь с частными производными
а его связь с частными производными
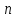 –го порядка выражается формулой
–го порядка выражается формулой
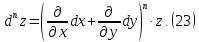
Замечание.
Если
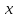 и
и
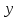 не независимые переменные, функции, то
формула (20) при
не независимые переменные, функции, то
формула (20) при
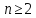 в общем случае неверна и, следовательно,
дифференциалы порядков
в общем случае неверна и, следовательно,
дифференциалы порядков
 функции
функции
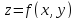 не обладают свойством инвариантности
формы.
не обладают свойством инвариантности
формы.
Рассмотренные определения дифференциалов высших порядков и их свойства распространяются и на функции с большим, чем два, количеством аргументов.
