
- •Основные понятия
- •Скалярное поле
- •Предел функции нескольких переменных
- •Дифференцирование функций нескольких переменных Частные производные
- •Условия дифференцируемости
- •Производная по направлению
- •Дифференцирование сложной функции
- •Инвариантность формы полного дифференциала
- •Нормаль и касательная плоскость к поверхности
- •Геометрический смысл полного дифференциала функции двух переменных
- •Производная функции, заданной неявно
- •Производные и дифференциалы высших порядков
- •Частные производные высших порядков
- •Дифференциалы высших порядков
- •Операторная форма дифференциалов высших порядков
- •Формула Тейлора
- •Экстремумы функций нескольких переменных Точки максимума и минимума
- •Необходимое условие экстремума
- •Достаточные условия экстремума
- •Условный экстремум
- •Методы нахождения условного экстремума Метод исключения переменных
- •Метод неопределенных множителей Лагранжа
- •Геометрический смысл условного экстремума функции:
- •Наибольшие и наименьшие значения
- •Составители
- •Функции нескольких переменных Методические указания к самостоятельному изучению соответствующего раздела курса математики для студентов всех специальностей
Дифференцирование сложной функции
Теорема
1.
Пусть функция
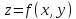 дифференцируема в точке
дифференцируема в точке
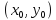 ,
а ее аргументы
,
а ее аргументы
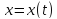 и
и
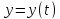 дифференцируемы в точке
дифференцируемы в точке
 , причем
, причем
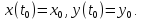
Тогда
сложная функция
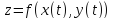 переменной
переменной
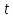 дифференцируема в точке
дифференцируема в точке
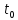 и
ее производная вычисляется по формуле
и
ее производная вычисляется по формуле
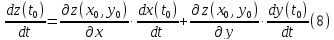
Доказательство.
Так как функции
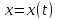 и
и
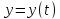 дифференцируемы в точке
дифференцируемы в точке
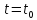 , то их приращения
, то их приращения
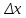 и
и
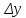 , соответствующее приращению аргумента
, соответствующее приращению аргумента
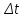 , представимы в виде:
, представимы в виде:
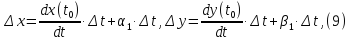
где
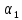 и
и
 — бесконечно малые функции при
— бесконечно малые функции при
 .
.
Так
как функция
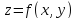 дифференцируема в точке
дифференцируема в точке
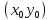 , где
, где
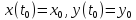 , то ее приращение
, то ее приращение
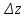 , соответствующее приращениям аргументов
, соответствующее приращениям аргументов
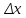 и
и
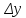 , представимо в виде
, представимо в виде

где
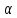 и
и
 — бесконечно малые функции при
— бесконечно малые функции при
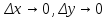 .
.
Из
дифференцируемости функций
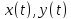 в точке
в точке
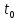 следует их непрерывность в этой точке,
т.е.
следует их непрерывность в этой точке,
т.е.
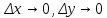 при
при
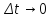 . Поэтому
. Поэтому
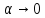 и
и
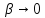 при
при
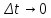 .
.
Подставляя выражения (9) в формулу (10), получаем
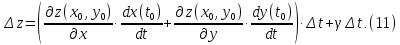
Здесь
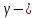 бесконечно малая функция при
бесконечно малая функция при
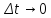 ,
имеющая вид:
,
имеющая вид:
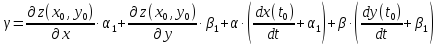
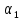 и
и
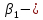 ранее показаны
ранее показаны
Обозначив
в (11) выражение в скобках буквой
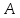 (
(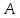 не зависит от
не зависит от
 ),
получаем
),
получаем
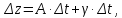
т.е.
приращение
 представлено как сумма линейной части
приращения
представлено как сумма линейной части
приращения
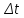 и бесконечно малой более высокого
порядка, чем
и бесконечно малой более высокого
порядка, чем
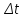 . Отсюда следуют дифференцируемость
сложной функции
. Отсюда следуют дифференцируемость
сложной функции
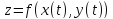 в
точке
в
точке
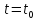 и формула (8) для
и формула (8) для
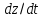 в этой точке. Теорема доказана.
в этой точке. Теорема доказана.
Аналогично формулируются и доказываются теоремы о дифференцируемости сложной функции любого числа переменных. Например:
Теорема
2.
Пусть функция
 дифференцируема в точке
дифференцируема в точке
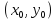 и ее аргументы
и ее аргументы
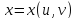 и
и
 дифференцируемы в точке
дифференцируемы в точке
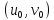 , причем
, причем
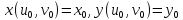 .
.
Тогда
сложная функция
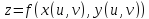 переменных
переменных
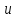 и
и
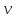 дифференцируема в точке
дифференцируема в точке
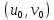 и ее частные производные вычисляются
по формулам
и ее частные производные вычисляются
по формулам
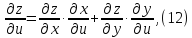
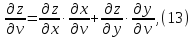
(Все производные в этих формулах вычисляются выполнены в соответствующих точках.)
Пример:
Найти
частные производные функции
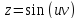 ,
,
где
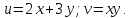 тогда в соответствии с (12 и 13) получим:
тогда в соответствии с (12 и 13) получим:
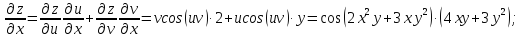
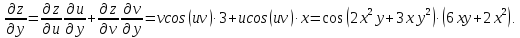
Инвариантность формы полного дифференциала
Пусть
функция
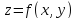 , где
, где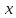 и
и
 — независимые переменные, дифференцируема
в некоторой точке
— независимые переменные, дифференцируема
в некоторой точке
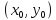 . Известно, что ее дифференциал в этой
точке определяется формулой
. Известно, что ее дифференциал в этой
точке определяется формулой
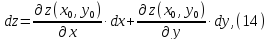
где
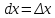 и
и
 — приращения независимых переменных
— приращения независимых переменных
 и
и
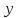 .
.
Пусть
теперь
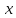 и
и
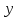 — не независимые переменные, а функции
— не независимые переменные, а функции
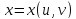 и
и
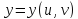 , дифференцируемые в точке
, дифференцируемые в точке
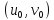 . Тогда по теореме 2 сложная функция
. Тогда по теореме 2 сложная функция
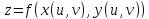 переменных
переменных
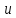 и
и
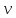 дифференцируема в точке
дифференцируема в точке
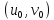 . Следовательно, ее дифференциал
определяется формулой
. Следовательно, ее дифференциал
определяется формулой

Подставляя
сюда
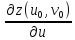 и
и
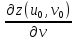 ,
определяемые формулами (12) и (13), и выполняя
простые преобразования, получаем
,
определяемые формулами (12) и (13), и выполняя
простые преобразования, получаем
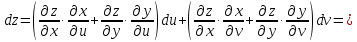
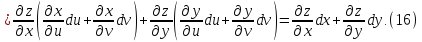
Таким
образом, дифференциал функции
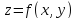 ,
когда
,
когда
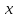 и
и
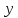 являются функциями, совпадает по форме
с дифференциалом функции
являются функциями, совпадает по форме
с дифференциалом функции
 , когда
, когда
 и
и
 — независимые переменные. Это свойство
называют инвариантностью2
формы первого дифференциала.
— независимые переменные. Это свойство
называют инвариантностью2
формы первого дифференциала.
Следует
иметь в виду, что в случае независимых
переменных
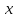 и
и
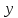 их дифференциалы
их дифференциалы
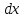 и
и
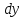 совпадают с приращениями
совпадают с приращениями
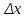 и
и
 .
В случае, когда
.
В случае, когда
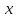 и
и
 сами являются функциями, их дифференциалы,
вообще говоря, не совпадают с приращениями
сами являются функциями, их дифференциалы,
вообще говоря, не совпадают с приращениями
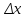 и
и
 , а являются лишь их линейными частями.
, а являются лишь их линейными частями.
Свойство инвариантности формы полного дифференциала распространяется на функции любого числа переменных.
Нормаль и касательная плоскость к поверхности
Пусть
дана некоторая поверхность, A
— фиксированная точка поверхности и B
— переменная точка поверхности,
 —
фиксированный вектор.
—
фиксированный вектор.
Обозначим
= (M)
— угол между векторами
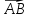 и
и
 (рис. 11).
(рис. 11).
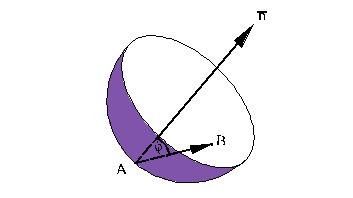
Рис.11
Ненулевой
вектор
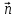
называется нормальным вектором к поверхности в точке A, если

Точка
поверхности
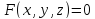 называется обыкновенной,
если в этой точке выполняются два
условия:
называется обыкновенной,
если в этой точке выполняются два
условия:
-
частные производные
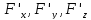 непрерывны;
непрерывны;
-
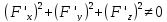 .
.
При нарушении хотя бы одного из этих условий точка поверхности называется особой точкой поверхности.
Теорема
1.
Если
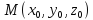 — обыкновенная точка поверхности
— обыкновенная точка поверхности
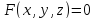 , то вектор
, то вектор
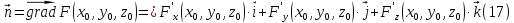
является
нормальным к этой поверхности в точке
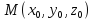 .
.
Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке.
Канонические уравнения нормали можно представить в виде
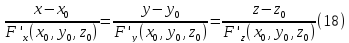
Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке.
Из этого определения следует, что уравнение касательной плоскости имеет вид:
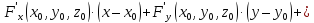

Если точка поверхности является особой, то в этой точке нормальный к поверхности вектор может не существовать, и, следовательно, поверхность может не иметь нормали и касательной плоскости.
