- •Основные понятия
- •Скалярное поле
- •Предел функции нескольких переменных
- •Дифференцирование функций нескольких переменных Частные производные
- •Условия дифференцируемости
- •Производная по направлению
- •Дифференцирование сложной функции
- •Инвариантность формы полного дифференциала
- •Нормаль и касательная плоскость к поверхности
- •Геометрический смысл полного дифференциала функции двух переменных
- •Производная функции, заданной неявно
- •Производные и дифференциалы высших порядков
- •Частные производные высших порядков
- •Дифференциалы высших порядков
- •Операторная форма дифференциалов высших порядков
- •Формула Тейлора
- •Экстремумы функций нескольких переменных Точки максимума и минимума
- •Необходимое условие экстремума
- •Достаточные условия экстремума
- •Условный экстремум
- •Методы нахождения условного экстремума Метод исключения переменных
- •Метод неопределенных множителей Лагранжа
- •Геометрический смысл условного экстремума функции:
- •Наибольшие и наименьшие значения
- •Составители
- •Функции нескольких переменных Методические указания к самостоятельному изучению соответствующего раздела курса математики для студентов всех специальностей
Предел функции нескольких переменных
Пусть
функция
 переменных
переменных
 определена
в некоторой окрестности точки
определена
в некоторой окрестности точки
 ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки
 .
.
Определение
1.
Число
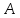 называется пределом
функции
называется пределом
функции
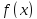 в точке
в точке
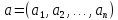 ,
если
,
если
ε
> 0) δε
> 0)
 x
Oδ(
x
Oδ(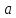 )
|f(x)
− A|
< ε
)
|f(x)
− A|
< ε
Обозначение:

В
пространстве
 предел функции
предел функции
 в точке
в точке
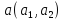 принято обозначать следующим образом:
принято обозначать следующим образом:
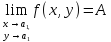
Замечания.
-
Определение предела функции
 переменных совпадает с определением
предела функции одной переменной,
только окрестность точки
переменных совпадает с определением
предела функции одной переменной,
только окрестность точки
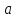 теперь не интервал
теперь не интервал
 ,
а
,
а
 мерный
открытый шар
мерный
открытый шар
(x1
−
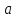 1)2
+ (x2
−
1)2
+ (x2
−
 2)2
+ … + (xn
−
2)2
+ … + (xn
−
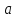 n)2
< δ2.
n)2
< δ2.
-
Если
 — граничная точка области определения
— граничная точка области определения
 функции
функции
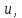 то определение предела уточняется
следующим образом (аналогично понятию
одностороннего предела функции одной
переменной):
то определение предела уточняется
следующим образом (аналогично понятию
одностороннего предела функции одной
переменной):
ε
>0) δε
> 0)
 (x
Oδ(
(x
Oδ(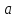 ))
∩ D(u)
|f(x)
− A|<ε.
))
∩ D(u)
|f(x)
− A|<ε.
Теорема
1.
Пусть функции
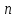 переменных
переменных
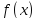 и
и
 ,
определены в области
,
определены в области
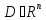 и
для некоторой точки
и
для некоторой точки
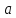
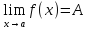
и
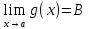
Тогда
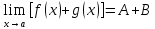
|
|
Теорема доказывается аналогично, как для функции одной переменной.
Определение
2.
Функция
 называется
бесконечно
малой
в точке
называется
бесконечно
малой
в точке
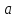 ,
если
,
если
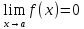
Определения и теоремы о бесконечно малых функций одной переменной справедливы для бесконечно малых функций нескольких переменных.
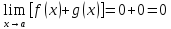
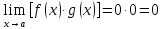
Пример: Найти пределы функций:
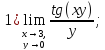
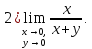
Решение: Убедившись, что функции не определены в предельной точке, сделав преобразования, находим:

так как
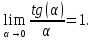
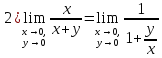
предел
не существует потому, что отношение
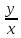 не имеет предела при произвольном
стремлении точки
не имеет предела при произвольном
стремлении точки
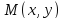 к точке
к точке
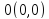 .
Так, приближаясь к
.
Так, приближаясь к
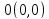 – началу координат по оси
– началу координат по оси
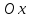 ,
где
,
где
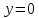 ,
получим
,
получим
 Если же приближаться к началу координат
по оси
Если же приближаться к началу координат
по оси
 ,
где
,
где
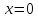 ,
то
,
то
 .
Таким образом при приближении
.
Таким образом при приближении
 к
к
 по разным направлениям функция имеет
разные придельные значения и, следовательно,
не имеет придела при
по разным направлениям функция имеет
разные придельные значения и, следовательно,
не имеет придела при
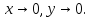
-
Покажем, что функция

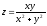
не
имеет предела при
 .
Действительно, если в качестве линии,
по которой точка
.
Действительно, если в качестве линии,
по которой точка
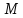 приближается к началу координат, выбрать
прямую
приближается к началу координат, выбрать
прямую
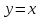 ,
то на этой прямой
,
то на этой прямой
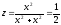 .
.
Если
же траекторией движения считать прямую
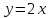 ,
то
,
то
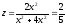 .
.
Следовательно,
предел в точке
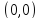 не существует.
не существует.
-
Найдем повторные пределы функции
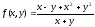
при
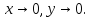
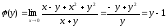 ,
,
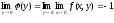 .
.
Если
же произвести предельные переходы в
обратном порядке, получим:
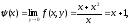

Таким
образом, повторные пределы оказались
различными (откуда следует, конечно,
что функция не имеет в точке
 предела в обычном смысле).
предела в обычном смысле).
Непрерывность функции нескольких переменных
Пусть
функция
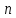 переменных
переменных
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
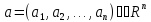 (включая
саму точку
(включая
саму точку
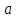 ).
).
Определение
1.
Функция
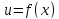 называется
непрерывной
в точке
называется
непрерывной
в точке
 ,
если она определена в точке
,
если она определена в точке


|
|
Обозначим приращения аргументов символами
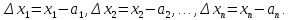 Соответствующее
приращение функции
Соответствующее
приращение функции
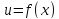
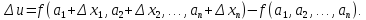
называется
полным
приращением функции
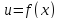 в точке
в точке
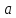 ,
соответствующая приращению
,
соответствующая приращению

Условие,
определяющее непрерывную функцию
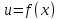 в
точке
в
точке
 аналогично
условию – функция определена в точке
аналогично
условию – функция определена в точке
 и
и
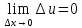
т.е. бесконечно малым приращениям аргументов, соответствует бесконечно малые приращения функции
|
|
Приращение функции вида
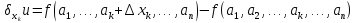
называется
частным
приращением функции
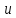 в точке
в точке
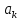 ,
соответствующая приращению
,
соответствующая приращению
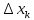 аргумента
аргумента
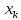 .
.
Определение
2.
Функция
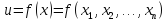 называется непрерывной
по переменной
называется непрерывной
по переменной
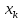 в точке
в точке
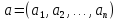 ,
если она определена в точке
,
если она определена в точке
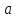 и
и

Свойства функций, непрерывных в ограниченной замкнутой области;
|
|
Теорема
1.
Если функция
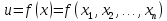 непрерывна в точке
непрерывна в точке
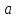 ,
то она непрерывна в этой точке по каждой
переменной
,
то она непрерывна в этой точке по каждой
переменной
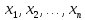 .
.
Обратное утверждение неверно.
Теорема
2.
Пусть функции
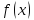 и
и
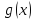 ,
определены в области
,
определены в области
 и непрерывны в точке
и непрерывны в точке
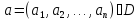 .
.
Тогда
функции
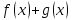 ,
,
 ·
·
 и
и
 (при
(при
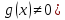 непрерывны в точке
непрерывны в точке

Доказательство вытекает из определения непрерывности функции в точке и теоремы о пределах суммы, произведения и частного двух функций.
Теорема 3. Всякая элементарная функция нескольких переменных непрерывна в области её определения.
Теоремы о свойствах функции одной переменной, непрерывной на отрезке, справедливы для функции нескольких переменных, непрерывной на замкнутом ограниченном множестве:
Теорема 4. Функция, непрерывная на замкнутой ограниченной области, ограничена на этой области.
Теорема 5 (Вейерштрасс). Функция, непрерывная в замкнутой ограниченной области, имеет наибольшее и наименьшее значение.