
- •Основные понятия
- •Скалярное поле
- •Предел функции нескольких переменных
- •Дифференцирование функций нескольких переменных Частные производные
- •Условия дифференцируемости
- •Производная по направлению
- •Дифференцирование сложной функции
- •Инвариантность формы полного дифференциала
- •Нормаль и касательная плоскость к поверхности
- •Геометрический смысл полного дифференциала функции двух переменных
- •Производная функции, заданной неявно
- •Производные и дифференциалы высших порядков
- •Частные производные высших порядков
- •Дифференциалы высших порядков
- •Операторная форма дифференциалов высших порядков
- •Формула Тейлора
- •Экстремумы функций нескольких переменных Точки максимума и минимума
- •Необходимое условие экстремума
- •Достаточные условия экстремума
- •Условный экстремум
- •Методы нахождения условного экстремума Метод исключения переменных
- •Метод неопределенных множителей Лагранжа
- •Геометрический смысл условного экстремума функции:
- •Наибольшие и наименьшие значения
- •Составители
- •Функции нескольких переменных Методические указания к самостоятельному изучению соответствующего раздела курса математики для студентов всех специальностей
Геометрический смысл полного дифференциала функции двух переменных
Пусть
функция
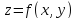 дифференцируема в точке
дифференцируема в точке
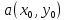 .
Ее графиком является поверхность
.
Ее графиком является поверхность
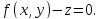
Положим
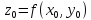 . Тогда точка
. Тогда точка
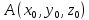 принадлежит поверхности.
принадлежит поверхности.
Частные
производные функции
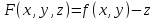 суть
суть
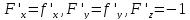
и
в точке
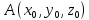 :
:
-
они непрерывны;
-
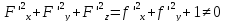 .
.
Следовательно,
 — обыкновенная точка поверхности
— обыкновенная точка поверхности
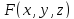 и в этой точке существует касательная
плоскость к поверхности. Согласно (19),
уравнение касательной плоскости имеет
вид:
и в этой точке существует касательная
плоскость к поверхности. Согласно (19),
уравнение касательной плоскости имеет
вид:
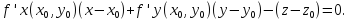
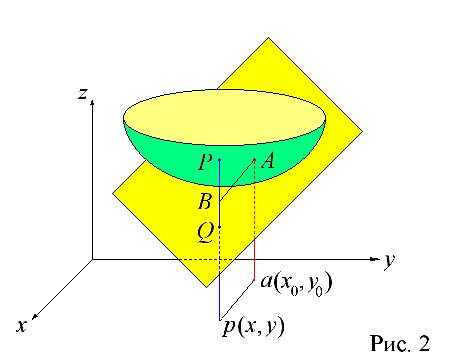
Рис.12
Вертикальное
смещение точки на касательной плоскости
при переходе из точки
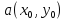 в произвольную точку
в произвольную точку
 есть
есть
 (рис. 12). Соответствующее приращение
аппликаты есть
(рис. 12). Соответствующее приращение
аппликаты есть
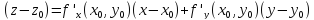
Здесь
в правой части стоит дифференциал
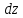 функции
функции
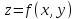 в точке
в точке
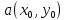 .
Следовательно,
.
Следовательно,
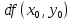 есть приращение аппликаты точки плоскости
касательной к графику функции
есть приращение аппликаты точки плоскости
касательной к графику функции
 в точке
в точке
 .
.
Из
определения дифференциала следует, что
расстояние между точкой
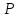 на графике функции и точкой
на графике функции и точкой
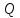 на касательной плоскости есть бесконечно
малая более высокого порядка, чем
расстояние от точки
на касательной плоскости есть бесконечно
малая более высокого порядка, чем
расстояние от точки
 до точки
до точки
 .
.
Неявные функции
Понятие и условия существования неявных функций
Функция
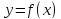 называется функцией,
заданной неявно (или неявной функцией)
если она задана уравнением
называется функцией,
заданной неявно (или неявной функцией)
если она задана уравнением
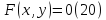
и
прямоугольной областью
 , если
, если
1)
 определена в
определена в
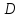 ;
;
2)
 уравнение
уравнение
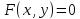 имеет единственное решение
имеет единственное решение
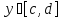 .
.
Иначе
говоря, уравнение (20) определяет функцию
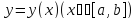 такую, что
такую, что
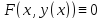 .
.
Аналогично определяют неявные функции любого числа переменных как функции, заданные уравнением и областью.
Условия существования неявной функции
Пусть:
функция

-
непрерывна в прямоугольной окрестности
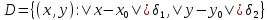
точки
 , причем
, причем
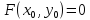 ;
;
-
функция
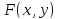 при каждом фиксированном
при каждом фиксированном
 строго монотонна по
строго монотонна по
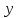 на интервале
на интервале
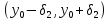 .
.
Тогда
существует окрестность точки
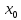 , в которой уравнение
, в которой уравнение
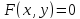 определяет функцию
определяет функцию
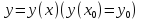 ,
непрерывную в этой окрестности.
,
непрерывную в этой окрестности.
Дифференцирование неявных функций
Теорема существования и дифференцируемости функции, заданной неявно
Теорема
1.
Пусть функция
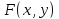 удовлетворяет условиям
удовлетворяет условиям
-
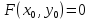 ;
;
-
частные производные
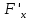 и
и
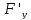 непрерывны
в некоторой окрестности точки
непрерывны
в некоторой окрестности точки
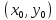 ;
;
-
 .
.
Тогда
-
уравнение
 определяет неявно в некоторой окрестности
точки
определяет неявно в некоторой окрестности
точки
 единственную непрерывную функцию
единственную непрерывную функцию
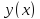 , удовлетворяющую условию
, удовлетворяющую условию
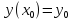 .
.
-
функция
 имеет производную, непрерывную в
окрестности точки
имеет производную, непрерывную в
окрестности точки
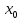 .
.
Выясним смысл условий теоремы.
Существование
непрерывной неявной функции
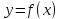 в окрестности точки
в окрестности точки
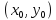 следует из теоремы существования, так
как:
следует из теоремы существования, так
как:
-
условие 1 гарантирует существование точки, координаты которой удовлетворяют уравнению
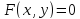 ;
;
-
из условия 2 следует непрерывность функции
 в окрестности точки
в окрестности точки
 , а из условия 3 — ее монотонность по
, а из условия 3 — ее монотонность по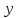 при каждом фиксированном
при каждом фиксированном
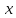 из этой окрестности.
из этой окрестности.
Следовательно,
условия 1–3 обеспечивают выполнение
условий существования неявной функции
 , удовлетворяющей условию
, удовлетворяющей условию
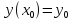 и непрерывной в окрестности точки
и непрерывной в окрестности точки
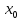 .
.
Производная функции, заданной неявно
Функция
 в окрестности точки
в окрестности точки
 обращает уравнение
обращает уравнение
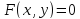 в тождество, т.е.
в тождество, т.е.
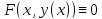
Дифференцируя
это тождество, получaeм
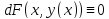 ,
а в силу инвариантности формы полного
дифференциала имеем
,
а в силу инвариантности формы полного
дифференциала имеем
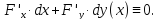
Отсюда получаем следующие формулы.
Дифференциал функции, заданной неявно:
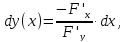
Производная функции, заданной неявно:
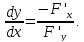
Теорема 1 обобщается для неявных функций любого числа переменных. Например:
Теорема
2.
Пусть функция
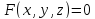 удовлетворяет условиям
удовлетворяет условиям
-
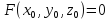 ;
;
-
частные производные
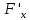 ,
,
 и
и
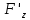 непрерывны в некоторой окрестности
точки
непрерывны в некоторой окрестности
точки
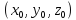 ;
;
-
 .
.
Тогда
-
уравнение
 определяет неявно в некоторой окрестности
точки
определяет неявно в некоторой окрестности
точки
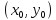 единственную непрерывную функцию
единственную непрерывную функцию
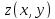 , удовлетворяющую условию
, удовлетворяющую условию
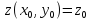 ;
;
-
функция
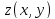 имеет
непрерывные частные производные в
окрестности точки
имеет
непрерывные частные производные в
окрестности точки
 , вычисляемые по формулам
, вычисляемые по формулам

