Мерой длительности переходного процесса является постоянная времени .

Постоянная времени равна промежутку времени, в течение которого свободная составляющая тока убывает в е раз.

Графически постоянная времени определяется длинной подкасательной к кривой тока при любом значении t.

Теоретически переходной процесс длится бесконечно долго, практически он заканчивается за время t=(45)

6.7. Включение цепи rc на постоянное напряжение

Рис. 6.4.

Определим переходное напряжение на ёмкости при подключении цепи RC в момент t=0 к источнику постоянного напряжения (рис. 6.4).

Расчёт будем вести в соответствии с вышеизложенным порядком расчёта (см. 6.5, 6.6).

1. U_C(-0)=0

2. Ri+u_C=E 

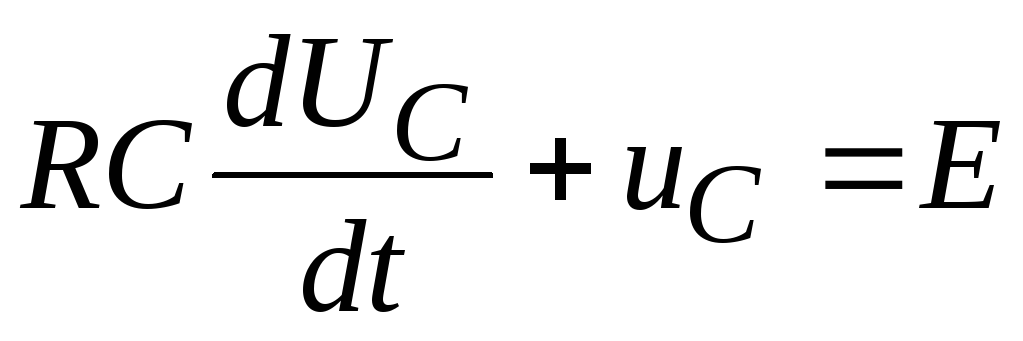
u_C=u_Спр +u_Ccв

3. u_Cпр=E

4. 

5.

При t=0 u_C(0)=E+A. По второму закону коммутации u_C(-0)=u_C(0)=0,

0=E+A  A=-E.

6.

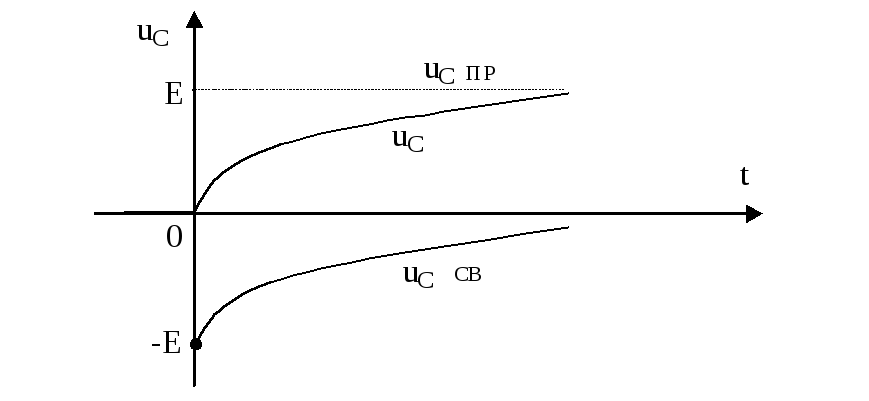
Рис. 6.5. Временная зависимость переходного напряжения на ёмкости.

6.8. Вопросы для самоконтроля к лекции 6

1. Какой процесс в ЭЦ называется переходным?

2. Сформулируйте законы коммутации и поясните их физический смысл

3. Какова сущность классического метода анализа переходных процессов?

4. Какой физический смысл имеет свободный режим?

5. Какой физический смысл имеет принужденный режим?

6. Как рассчитываются токи и напряжения ЭЦ в свободном и установившемся режимах?

7. Какова последовательность расчёта переходного процесса классическим методом?

8. Разберите решение задач 8.4,8.9,8.18,8.26 из [4].

9. Решите задачи 8.7, 8.16 из [4].

Литература: [1] с. 185-198; [2] с. 103-112; [3] с. 199-209; [5] с. 344-363. Лекция 7. Операторный метод расчёта переходных процессов

7.1. Преобразования Лапласа

Расчёт переходных процессов классическим методом сводится к решению дифференциальных уравнений. При этом основные трудности решения заключаются в определении постоянных интегрирования. По мере усложнения ЭЦ и соответственно повышения порядка дифференциальных уравнений эти трудности увеличиваются.

Более удобным является метод решения линейных дифференциальных уравнений, при котором заданные начальные условия включаются в исходные уравнения и не требуется определять постоянные интегрирования. Таким методом является операторный метод.

В основе операторного метода лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область функции комплексного переменного р=с+j, где операции принимают более простой вид: вместо интегродифференциальных уравнений получаются алгебраические уравнения (7.1) (7.2)

Различают прямое и обратное преобразование Лапласа. Функция f(t) определена при t0 и при t<0 f(t)=0

(7.1)

(7.2)

Функция f(t) называется оригиналом, F(p)- её изображением. Фразу «оригинал f(t) имеет своим изображением F(p)» будем заменять символически с помощью знака соответствия 

f(t)  F(p) или F(p) f(t).

7.2. Некоторые свойства преобразования Лапласа

1. Изображение постоянной величины

. (7.3)

Пример:

,

2. Свойство линейности

(7.4)

Пример:

i₁I₁(p); i₂I₂(p); i₁R₁+i₂R₂ I₁(p)R₁+I₂(p)R₂

3. Дифференцирование оригинала f(t)

f’(t) pF(p) - f(0) - при ненулевых начальных условиях (7.5)

f’(t) pF(p) - при нулевых начальных условиях

Пример: i I(p)

.

4. Интегрирование оригинала

(7.6)

Пример: i I(p)

.