Лекция 4. Символический метод расчета цепей гармонического тока

Метод, основанный на символическом изображении синусоидальных функций времени комплексными величинами, называют символическим (комплексным) методом или методом комплексных амплитуд.

4.1. Символическое изображение синусоидальных функций комплексными величинами

Любую гармоническую функцию можно изобразить в виде вектора (рис. 4.1, а), а каждому вектору можно поставить в соответствие комплексное число (рис. 4.1, б).

1. б )

Рис. 4.1.

Существуют три формы записи комплексного числа

1. - показательная (А - модуль комплексного числа, - его аргумент);

2. - тригонометрическая;

3. - алгебраическая (а - вещественная часть, б - мнимая

часть).

Переход от одной формы записи к другой можно осуществить с помощью формул:

; ; (4.1)

; .

Необходимо запомнить:

; ; ; . (4.2)

Комплексной амплитудой называется комплексная величина, модуль которой равен амплитуде синусоидального тока, а аргумент - начальной фазе.

В раз меньшую величину называют комплексным действующим

значением - комплексным током.

Аналогично

- комплексная амплитуда напряжения;

- комплексное напряжение.

Составим новое комплексное число

(4.4)

(4.3)

которое называется вращающимся вектором тока.

Разложим по формуле Эйлера:

(4.5)

Следовательно, синусоидальный ток является мнимой частью вращающегося вектора, т.е.

,

где j - знак мнимой части.

Часто величины i, u, называют оригиналами, а – их комплексными изображениями. Примеры:

1. ;

2. ;

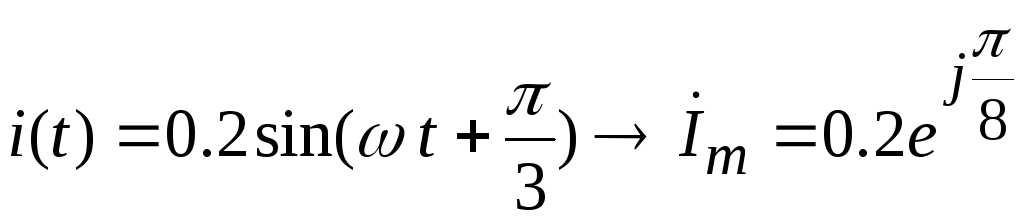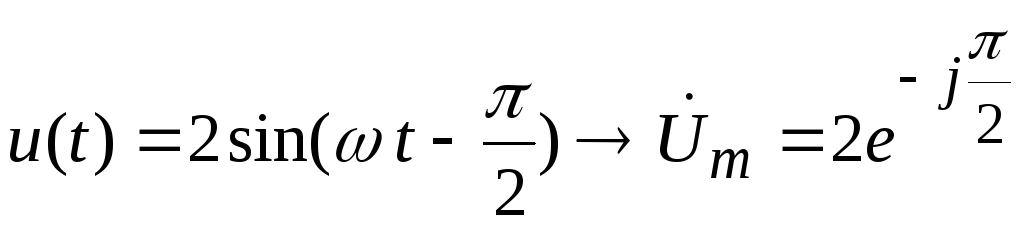3) .

4.2. Изображение производной и интеграла от синусоидальной функции

Пусть , где знак соответствия,

Тогда

, т.е.

Операция дифференцирования синусоидальной функции соответствует умножению на ее комплексного изображения.

Пример: С производной мы встречаемся при определении напряжения на индуктивности

При - для вращающихся векторов получим:

,

откуда имеем .

При этом получаем комплексное сопротивление индуктивности , как чисто мнимое число.

При , (4.7)

т.е. - операция интегрирования синусоидальной функции

соответствует делению на j ее комплексного изображения.

Пример: С интегралом мы встречаемся при определении напряжения

на емкости

.

Для вращающихся векторов получим

,

откуда имеем,

- комплексное cопротивление емкости (4.8)

Пример: Рассмотрим цепь RLC (рис.4.2.).

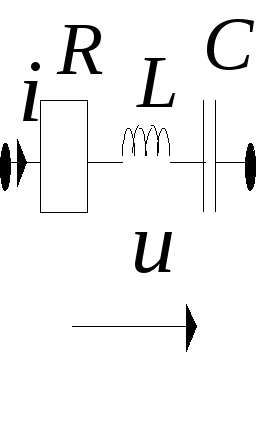
Рис. 4.2.

Уравнение цепи для мгновенных значении напряжений имеет вид:

При для комплексных зображений получим

.

4.3. Комплексные сопротивления и проводимость

Комплексным сопротивлением называется отношение комплексного напряжения к комплексному току :

(4.9)

Используя формулу Эйлера, получим

(4.10)

где - модуль комплексного сопротивления, равный полному сопротивлению цепи;

- аргумент комплексного сопротивления;

R и Х - активное и реактивное сопротивление цепи.

Комплексной проводимостью называется величина, обратная комплексному сопротивлению

; (4.11)

; ;

Y, G, В - полная , активная, реактивная проводимость.

Очевидна следующая связь , используя которую можно установить зависимость между эквивалентными сопротивлениями и проводимостями ЭЦ. При заданном комплексном сопротивлении некоторого участка цепи можно определить комплексную проводимость того же участка:

(4.12)

Если задана комплексная проводимость некоторого участка ЭЦ, то комплексное сопротивление того же участка равно

. (4.13)