§30. Теорема Стокса.

- теорема Стокса

- Теорема Гаусса в операторной форме

Например

- теорема Стокса в операторной форме.

Задачи

1. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:

,

если объем, который охватывает замкнутая поверхность, равен V; A – постоянный вектор.

Решение. Умножим искомый интеграл на постоянный вектор р:

Так как вектор р произволен, то

.

Аналогично показывается, что

§31. Функциональные соотношения различных полей

Здесь - диэлектрическая проницаемость, а - диэлектрическая восприимчивость.

-разложение функции в ряд Маклорена.

Если же :

Возможно разложить по векторам в ряд Маклорена:

Первое слагаемое – это индукция, связанная с собственным дипольным моментом в отсутствие внешнего поля (собственная поляризация) – пироэлектрики.

Второе слагаемое – линейные среды.

Третье слагаемое – учёт нелинейности среды.

Среды, для которых нелинейные члены в разложении индукции по полю имеют вес, называются нелинейными.

Линейные среды

Введём обозначение: , тогда

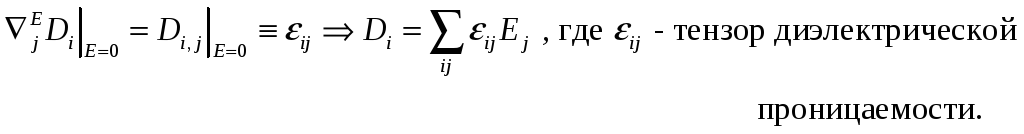
Аналогично вводятся тензоры:

Для ферромагнетиков - учёт нелинейности.

Неоднородные среды

Среды, для которых материальные характеристики () являются функциями координат.

Т.е. характеристики трансляционно неинвариантны.

Введём понятие сплошной среды. Сплошная среда – это среда в каждой точке которой измерение материальных характеристик даёт не нулевой результат. Сплошная среда – это модель. В реальной среде имеются микро-пустоты, т.е. вещество локализовано в некоторых точках пространства. Чтобы перейти к сплошной среде, нужно усреднить микро-параметры по достаточно большому объёму.

Анизотропные среды

Анизотропные среды (свойства), это такие среды, свойства которых зависят от направления, в котором это свойство измеряется.

Пусть в каком-то направлении исследуются оптические свойства среды. Затем мы повернули направление исследования, и оптические свойства изменились, т.е. оптические свойства зависят от угла поворота.

Так как свойства меняются, то они неинвариантны относительно вращения. Этим свойством обладает всякая анизотропная среда.

Для тензоров 2-го ранга есть исключения:

Кубические системы описываются тензорами изотропного вида, т.е.

Монокристалл – есть однородная анизотропная среда.

§32*. Условия на границе раздела двух сред.

Рассмотрим поведение электромагнитного поля при переходе через границу раздела двух сред с различными материальными характеристиками. Используем теорему Остроградского-Гаусса и теорему Стокса:

Теорема Остроградского-Гаусса:

т.е. совершается следующий переход:

Теорема Стокса:

Запишем первое и четвёртое уравнения Максвелла в среде:

Имеется граница раздела – поверхность, отделяющая одну среду от другой.

- нормаль к поверхности.

- скачок функции на границе раздела двух сред.

Рассмотрим цилиндр, образующие которого перпендикулярны поверхности . По объёму проинтегрируем первое и уравнение Максвелла:

Воспользуемся теоремой Остроградского-Гаусса:

При а следовательно и

В последнем равенстве мы воспользовались теоремой о среднем.

Аналогично:

Тогда:

Где ~h – боковая поверхность

В пределе, при ,

- заряд на поверхности раздела двух сред

Пусть в пределе , при этом

Поверхностная плотность заряда:

В результате получаем:

Если на поверхности нет свободных зарядов, то и , т.е. - непрерывна.

Аналогично рассмотрев второе уравнение Максвелла

Получим

Т.е. - всегда непрерывна, её скачок всегда равен нулю.

Теперь рассмотрим четвёртое уравнение Максвелла

, причём

Тогда по теореме Стокса:

Рассмотрим правую часть этого равенства:

Второе слагаемое, при даёт 0.

- ток, протекающий через поверхность , причём ток положителен в направлении нормали

При ,

Воспользуемся теоремой о среднем:

Рассмотрим предельный переход при , тогда

- поверхностный ток, текущий через перпендикулярно чертежу.

При - ток, текущий по поверхности, в расчёте на длину.

В результате получаем:

Если , то - непрерывна.

Аналогично для третьего уравнения Максвелла:

Имеем:

Т.е. тангенциальная составляющая электрического поля непрерывна.

Определим

тогда

Ввиду произвольности , это выражение эквивалентно выражению: