1. Ма́трица - матрицей называется прямоугольная таблица из чисел aij , i = 1,2,…m,j = 1,2,…n , состоящая из m строк и n столбцов.

Суммой матриц(А+В) A = (aij) и B = (bij) называется матрица С = (cij) того же порядка.каждый элемент которой равен сумме соответственных элементов матриц А и В

Произведением матрицы А = (aij) на число а наз. Матрица В=(bij) ,получающаяся из матрицы А умножением всех ее элементов на а.

Произведением матрицы А на матрицу В называется матрица С,элемент которой сij,стоящий в i-й строке и j-м столбце,равен сумме произведений соответственных элементов i-ой строки матрицы А и j-го столбцо матрицы В

2 Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

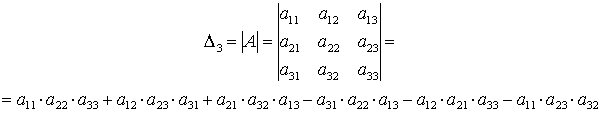
Определители 3-ого порядка вычисляются по правилу Саррюса: Первые три слагаемые берутся со знаком плюс и определяются из элементов главной диагонали, а последующие три слагаемые берутся со знаком минус и определяются из элементов побочной диагонали.

Под перестановкой множества S понимается множество этих же чисел, упорядоченное некоторым другим образом.

Перестановка называется транспозицией, если переставляются местами только два элемента множества, тогда как остальные элементы остаются на своих местах.

Пример перестановки:

Пример транспозиции

Теорема: Транспозиция меняет четность перестановки.

Доказательство. Рассмотрим сначала случай, когда транспонируемые символы i и j

стоят рядом, т.е. перестановка имеет вид ..., i, j, ..., где многоточия заменяют те симво-

лы, которые не затрагиваются транспозицией. Транспозиция превращает нашу пере-

становку в перестановку ..., j, i, ..., причем, понятно, в обеих перестановках каждый из

символов i, j составляет одни и те же инверсии с символами, остающимися на месте.

Если символы i и j раньше не составляли инверсии, то в новой перестановке

появляется одна новая инверсия, т.е. число инверсий увеличивается на единицу; если

же они раньше составляли инверсию, то теперь она пропадает, т.е. число инверсий на

единицу уменьшается. В обоих случаях четность перестановки меняется.

Пусть теперь между транспонируемыми символами i и j расположены s символов,

s > 0, т.е. перестановка имеет вид

..., i, k1, k2, ..., ks, j, ... (1)

Транспозицию символов i и j можно получить в результате последовательного выпол-

нения 2s+1 транспозиций соседних элементов. А именно это будут транспозиции, пе-

реставляющие символы i и k1, затем i (уже стоящие на месте символа k1) и k2 и т.д.,

пока i не займет место символа ks. За этими s транспозициями следует транспозиция,

перемещающая символы i и j, а затем s транспозиций символа j со всеми k, после чего j

занимает место символа i, а символы k возвращаются на свои старые места. Таким об-

разом, мы нечетное число раз меняли четность перестановки, а поэтому перестановки

(1) и

..., j, k1, k2, ..., ks, i, ...

имеют противоположные четности.

Следствие: Перестановка четна тогда и только тогда, когда она разлагается в произведение четного числа циклов длины 2.

Определителем (детерминантом) n– го порядка или определителем (детерминантом) квадратной матрицы n– го порядка называют алгебраическую сумму всех членов определителя данной матрицы, взятых со своими знаками.

Свойства определителей:

1. det A^T = det A. Это означает равномерность строк и столбцов

2) Если в определителе поменять местами 2 строки(столбца), то он поменяет знак

3) Если в определителе имеются 2 одинаковые(пропорциональные) строки (столбца), то он равен 0

4) Если элементы какой-либо строки (столбца) умножить на z, то определитель

умножится на z

5)Если все элементы какой-либо строки (столбца) равны нулю, то он сам равен нулю

6)Если к элементам какой-либо строки (столбца) прибавить соответственно элементы

другой строки (столбца), умноженные на z0, то определитель не изменится

7) Сумма произведений элементов любой строки(столбца) определителя на соответствующие алгебраические дополнения этой строки(столбца) равна этому определителю

8) Сумма произведений какой-либо строки(столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки(столбца) равна нулю

3. Минором некоторого элемента аij , определителя матрицы n - ого порядка называется

определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент аij. Обозначается Мij.

Алгебраическим дополнением элемента аij называется его минор, взятый со знаком "+", если сумма (i + j) четное число, и со знаком "-", если эта сумма нечетное число. Обозначается Аij.

Разложение определителя по строке или столбцу

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки

d = ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i = )

или j- го столбца

d = a1 j A1 j + a2 j A2 j +... + an j An j (j = ).

В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

4. Теорема Лапласа — одна из теорем линейной алгебры, которая позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения. Теорема используется для вычисления определителя квадратной матрицы.

Отметим, что сумма произведений элементов какого-либо ряда на алгебраические дополнения элементов другого, но параллельного исходному ряда, всегда равна нулю.

5. Невырожденная линейная сис-ма A∙ X = B(detA≠0),то сис-ма имеет решение и при том единственное. Это решение задается формулами:

6. Система m уравнений с n неизвестными в общем виде записывается следующим образом:

,

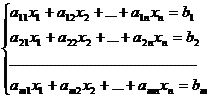где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Определение. Если b1, b2, …,bm = 0, то система называется однородной. однородная система всегда совместна, т.к. всегда имеет нулевое решение.

Матричная форма:

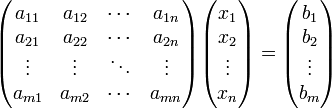или Ax = B

Критерий совместности линейных уравнений :

Система совместна тогда и только тогда, когда rank A = rank D.

7. РАНГ МАТРИЦЫ — наивысший из порядков отличных от нуля миноров этой матрицы.

Теорема: при элементарных преобразованиях ранг матрицы не меняется.

Доказательство:

1. Mr+1 * Mr+1=0. 2. Mr+1   Mr+1 = 0. 3. Mr+1 = (Mr+1=0)+(Mr+1=0)=0. (rg не увеличивается, но и не уменьшается, так как преобразования обратные к элементарным также являются элементарными) ч.т.д

линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу.

Теорема о ранге матрицы:

ранг матрицы равен максимальному числу ее линейно-независимых строк или столбцов,через которые линейно выражаются все остальные строки(столбцы)

8. метод Гаусса - Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Под названием "метод Гаусса" существует целая группа методов решения этой задачи. Несколько методов основаны на разложении матрицы A в произведение двух треугольных матриц и, возможно, одной-двух матриц перестановок. При этом одновременно с разложением или после него может выполняться также преобразование правой части - вплоть до искомого решения.

представление матрицы A в виде LU, где L — нижняя треугольная матрица, а U — верхняя треугольная матрица. LU-разложение еще называют LU-факторизацией.

LU-разложение используется для решения систем линейных уравнений и для обращения матриц. Этот метод является одной из разновидностей метода Гаусса

9. Обратная матрица - это матрица результатом умножения на которую исходной матрицы является единичная матрица.

Метод Гаусса, с помощью матрицы алгебраических дополнений, Использование LU разложения.

10. Линейное уравнение называется однородным, если его свободный член равен нулю.

Система линейных уравнений называется однородной, если все входящие в нее уравнения являются линейными однородными уравнениями.

Однородная система n линейных уравнений с n неизвестными имеет ненулевые решения тогда и только тогда, когда определитель ее равен нулю.

Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.

11. Линейное пространство - математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трехмерного пространства.

типичные примеры линейных пространств.

Пример 1. Линейное пространство векторов на плоскости (или в трехмерном пространстве) с обычными операциями сложения векторов и умножения вектора на действительное число. Нулевым элементом является нулевой вектор.

Пример 2. Линейное пространство всевозможных последовательностей комплексных чисел с операциями

Нулевой элемент - последовательность (0, 0, ..., 0, ...).

Пример 3. Линейное пространство функций, непрерывных на данном отрезке с обычными операциями сложения функций и умножения функции на действительное число. Нулевой элемент - функция .

Ба́зис — набор n векторов в n-мерном линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их линейной комбинации, при этом ни один из базисных векторов не представим в виде линейной комбинации остальных.

Размерность — это количество векторов в базисе данного линейного подпространства, максимальное количество линейно-независимых векторов.

Матрица перехода от старого базиса к новому образована координатами векторов нового базиса в старом.

12. лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений.

Действия над линейными операторами:

Сложение

Умножение на число

Умножение операторов

Возведение в целую положительную степень

13. Преобразование матрицы оператора ^

A

при переходе от "старого" базиса e к "новому" базису f определяется формулой:

Af = C −1 Ae C

Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.

14. Ненулевой вектор называется собственным вектором оператора A, если оператор A переводит в коллинеарный ему вектор, то есть . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору .

Теорема. Характеристический многочлен линейного оператора не зависит от выбора ба­зиса (одинаков для всех базисов).

Доказательство. Пусть в пространстве Kⁿ дан линейный оператор j и даны два базиса (u) и (v). Пусть также C − матрица перехода от первого базиса ко второму. Соответственно матрицы нашего линейного оператора в этих двух базисах обозначим A = и B = . Тогда

det (B − λE) = det (C⁻¹AC − C⁻¹(λE)C) = det (C⁻¹(A − λE)C) = det C⁻¹×det (A − λE)×det C =

= det (A − λE), QED.