Список заданий:

Задание 1: Определить, на какие углы отклонятся шары после удара, счи­тая удар абсолютно упругим. Результаты вычислений прове­рить экспериментально и занести в таблицу. Рассмотреть два случая:

а) большой шар бьет по маленькому шарику, который покоит­ся;

б) маленький шар бьет по большому шару, который покоится.

Задание 2: Экспериментально определить время взаимодействия шаров и рассчитать силу удара.

Задание 3: Считая удар реальным, определить коэффициент восстановле­ния. Необходимые данные взять из задания 1.

Лабораторная работа №5 «гармонические колебания».

Цель работы: изучение гармонического колебательного движения.

Вопросы для допуска к работе:

1. Что называют колебаниями? Какие колебания называются свободными гармоническими колебаниями?

2. При каких условиях возникают гармонические колебания?

3. Каким уравнением описываются гармонические колебания?

4. Что называют амплитудой, частотой, циклической частотой, фазой, начальной фазой, периодом гармонических колебаний? В каких единицах измеряются эти величины?

5. Какие колебания называются затухающими? При каких условиях они возникают?

6. Каким уравнением описываются затухающие колебания?

7. Что называют коэффициентом затухания, логарифмическим декрементом затухания, добротностью затухающих колебаний? В каких единицах измеряются эти величины?

8. Чем определяется период затухающих колебаний?

9. Что называют математическим маятником?

10. Чем определяется период математического маятника?

11. Что называют физическим маятником?

12. Чем определяется период физического маятника?

13. Что называют приведенной длиной физического маятника?

14. Что называется моментом инерции твердого тела, относительно неподвижной оси?

15. Как рассчитать момент инерции физического маятника, состоящего из диска, закрепленного на стержне?

16. Как определить расстояние от точки подвеса до центра масс физического маятника, состоящего из диска, закрепленного на стержне?

17. От чего зависит кинетическая, потенциальная и полная энергии тела, совершающего гармоническое колебательное движение?

Список рекомендуемой литературы:

Основная

1. Савельев И.В. Курс общей физики. - М., 1962, т.1, с. 176 -190.

2. Сивухин Д.В. Общий курс физики: Т.1. Механика. - М., 1974. (гл. 6), с. 204-215.

3. Яворский Б.И., Пинский А.А. Основы физики. - М., 1972, т.2, с. 185-190.

Дополнительная

1. Берклеевский курс физики: Т.1. Механика. - М., 1975, с. 219 -246.

Краткая теория

Гармоническими колебаниями называются такие движения, ко­торые описываются уравнениями или , где х - смещение материальной точки от положения равновесия, - циклическая частота, показы­вающая число колебаний, совершаемых материальной точкой за 2 единиц времени; А - амплитуда, характеризующая наибольшее возможное смещение колеблющейся точки от положения равновесия; ( ) - фаза колебания, позволяющая определить, где нахо­дится в данный момент времени материальная точка, куда движет­ся, сколько полных колебаний совершила до рассматриваемого мо­мента; ₁ и ₂ - постоянные (начальные фазы), зависящие от условий в начальный момент отсчёта; Т - период.

Скорость материальной точки, совершающей гармоническое колебательное движение описыва­емое уравнением , зависит от времени следующим образом:

Ускорение:

.

Ускорение материальной точки, совершающей гармоническое колебательное движение, пропорцио­нально смещению и направлено в противоположную сторону (нахо­дится в противофазе). Из этого следует, что рассматриваемое движение материальной точки происходит под действием силы про­порциональной смещению. К таким силам, в первую очередь, относятся упругие силы, которые пропорциональны смещению х и направ­лены в противоположную ему сторону: .

Силы не упругие по своей природе, но аналогичные им по виду зависимости от смещения, называются квазиупругими.

Напишем уравнение движения материальной точки, на которую действуют упругие или квазиупругие силы: (1). Итак, или .(В случае квазиупругих сил под "k" будем понимать коэффициент, объединяющий все постоянные величины в выражении силы, дейст­вующей на систему, выведенную из положения равновесия). Если обозначить через ², то уравнение (1) можно переписать (1'). Решение уравне­ния (1') имеет вид , или (убедитесь с помощью подстановки, что эти решения удовлетворяют уравнению (1)), где (2), откуда следует (3). Равенство (3) позволяет рассчитать период для различных гармонических колебательных движений, обусловленных упругими и квазиупругими силами.

Амплитуда А и начальная фаза не могут быть определены из дифференциального уравнения. Эти постоянные определяются началь­ными условиями, например, начальными значениями смещения х и скорости .

Совершающая колебания материальная точка обладает скоростью, а, следовательно, и кинетической энергией. Кроме того, колеблющаяся точка будет обладать и потенци­альной энергией. . Полная энергия .

(Выведите этот результат самостоятельно).

Изложенные выше рассуждения были сделаны при допущении, что кроме упругих или квазиупругих сил никакие силы на материальную точку не действуют. На практике всякое колебание си­стемы, которое не поддерживается извне, затухает, амплитуда ее колебания с течением времени уменьшается. Причина затуха­ния обусловливается силами, тормозящими движение. При учёте этих сил в уравнение движения необходимо добавить слагаемое, определяющее величину сил сопротивления.

Рассмотрим случай колебания в вязкой среде. Будем считать, что скорости не слишком велики, поэтому , где r - коэффициент сопротивления. Тогда уравнение движения мо­жет быть написано в виде: (4). Введем обозначения . Тогда уравнение (4) примет вид:

. (5)

Решение уравнения (5), описывающее движение материаль­ной точки под действием упругой или квазиупругой силы в среде с сопротивлением, имеет вид: , или , где (6) - амплитуда, уменьшающаяся с течением времени, а , или (7). Период колебания в среде с сопротивлением больше, чем период колебания точки такой же массы m под действием такой же упругой или квазиупругой силы в среде без сопротивления.

Логарифм отношения двух последовательных значений ампли­туд, отстоящих друг от друга на время, равное периоду Т, на­зывается логарифмическим декрементом затухания:

=. .(8)

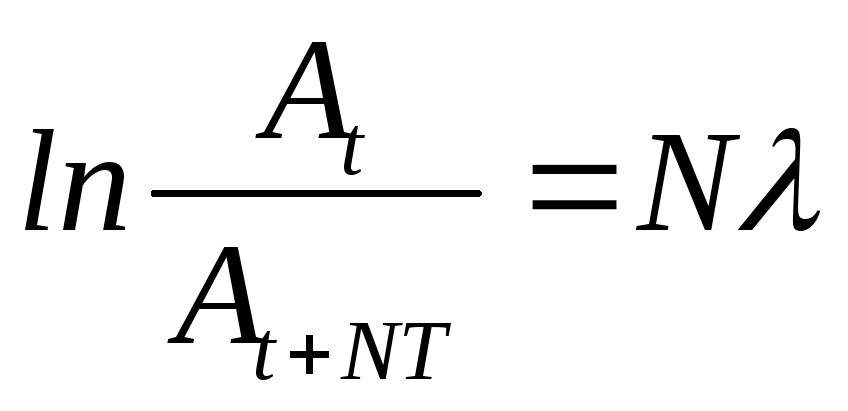Если взять несколько колебаний, то , а . При (e = 2,718), N = 1.

Таким образом, величина обратная декременту , равна числу колебаний, через которое амплитуда колебаний уменьшит­ся в e раз.

Зная , можно, пользуясь соотношением определить коэффициент сопротивления r.

Для характеристики колеблющейся системы часто применяется величина Q, называемая добротностью. Эта величина представляет собой умноженное на 2 отношение запасенной энергии к среднему значению энергии, теряемому за один период (при незначительном затухании). Можно показать, что доброт­ность связана с логарифмическим декрементом затухания следую­щим соотношением: . (9)

Рассмотрим примеры гармонических колебательных движений.

Пример I. Определение периода колебаний физического маятника.

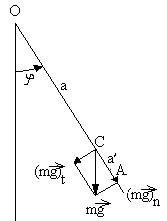
Физическим маятником называется твер­дое тело, которое может качаться вокруг неподвижной горизон­тальной оси. Точка пересечения её с вертикальной плоскостью, проходящей через центр масс маятни­ка С, называется точкой подвеса маятника (рис.1).

Рис.1

Положение тела в любой момент времени можно охарак­теризовать углом отклонения его из положения равновесия . Рассмот­рим решение при малых углах отклонения.

Силу тяжести mg можно счи­тать приложенной к центру масс С. Момент составляющей силы тяжести сообщает телу угловое ускорение , равное , (10)

где J - момент инерции тела относительно оси 0. Подставив в (10) выражения для  и (при малых углах откло­нения), получим: . Это уравнение вполне аналогич­но уравнению (1). Откуда мы получаем: при малых углах отклоне­ния тело будет совершать около положения равновесия гармоническое колебательное движение с циклической частотой и периодом

(11).

Колебания физического маятника изохронны (период колеба­ний не зависит от амплитуды), когда угловая амплитуда колебаний не превышает несколько градусов. При больших амплитудах изохронность нарушается.

Пример 2: Определение периода колебаний математического маятника.

Математическим называется маятник, вся масса которого практически сосредоточена в одной точке - в центре масс маятника С. Примером математического маятника мо­жет служить шарик, подвешенный на длинной нити.

Математический маятник можно рассматривать как частный случай физического маятника: a = l, где l - длина маятника. Тогда формула (11) переходит в . (12)

Сравнивая формулы (11) и (12), заключаем, что физичес­кий маятник колеблется с таким же периодом, как математичес­кий маятник с длиной (13), которая называется при­веденной длиной физического маятника.