6.3. Особые точки передаточной функции.

Операторная передаточная функция T(p), как правило, имеет вид правильной рациональной дроби вида (6.7). Однако, если разложить числитель и знаменатель на множители, то передаточную функцию можно записать в виде

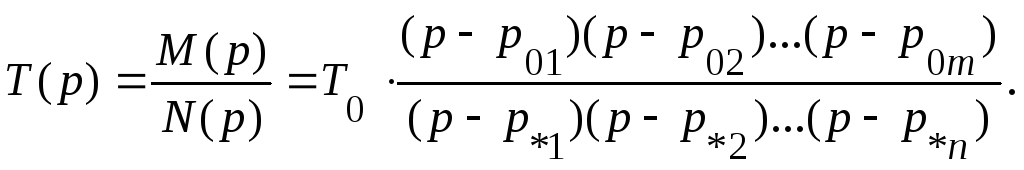(6.11)

Здесь p₀₁, p₀₂ , …p_0m – корни уравнения числителя M(p) = 0. Их называют нулями функции T(p).

Корни уравнения знаменателя N(р) = 0 p_*1, p_*2, …p_*n называются полюсами функции T(p).

Нули и полюсы функции (6.11) являются особыми точками, по которым можно, в частности, оценить диапазон частот, в пределах которого рассчитываются частотные характеристики.

Графическое изображение нулей и полюсов функции на плоскости операторной переменной

р = s + jω называется диаграммой или картой нулей и полюсов (рис. 6.5). Вещественную и мнимую оси обозначают соответственно s и ω, нули изображают кружочками, а полюсы - крестиками. Масштаб по обеим осям должен быть одинаковым.

Пример 6.3. Рассчитать нули и полюсы передаточной функции (6.10), полученной в примере 6.2, и построить диаграмму особых точек.

Решение.

.

Р

ассчитаем нули и полюсы передаточной функции

Числитель M(p) = p + 10⁴ = 0. p₀₁ = 10⁴  нуль.

З

наменатель N(p) = p² + 1.1·10⁷ p + 10¹⁶ = 0.

p_*1,2 = (-5.5·± j8.35)·10⁶ – два полюса.

При построении карты нужно соблюдать одинаковый масштаб по действительной и мнимой осям, как это сделано на рис. 6.5.

6.4. Вывод формул частотных характеристик функции

Для получения аналитических выражений частотных характеристик передаточной функции производят в формуле (6.7) обратную замену переменных p = jω и группируют действительные и мнимые части числителя и знаменателя

,

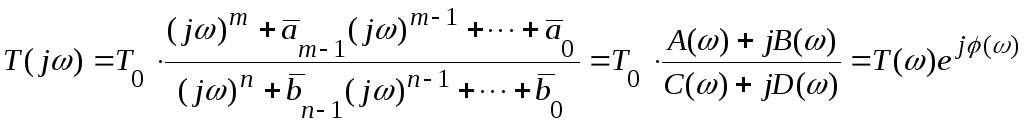где A(ω), C(ω) – действительные, B(ω), D(ω) – мнимые части; T(ω) – модуль, φ(ω) – аргумент передаточной функции.

В

ыражением АЧХ является модуль T(ω) функции T(jω)

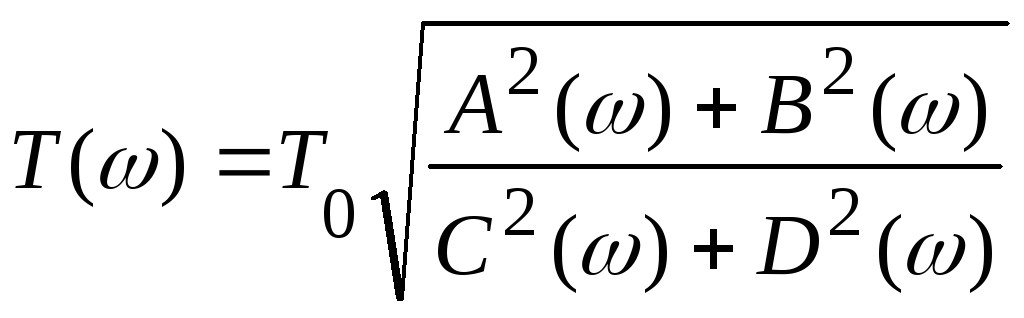. (6.12)

Выражением ФЧХ является аргумент φ(ω) функции T(jω). Аргумент можно получить в виде разности аргументов числителя φ_числ(ω) и знаменателя φ_знам(ω) комплексной функции передачи

. (6.13)

Как известно из теории комплексных чисел формула аргумента φ(ω) комплексного числа M(jω) = A(ω) + jB(ω) зависит от знака действительной A() и мнимой B() частей, т.е. от положения точки M(jω) на комплексной плоскости (рис. 6.6):

Если точка находится в первой или во второй четвертях, то угол измеряется от действительной оси против часовой стрелки; если в третьей или в четвертой – то от действительной оси по часовой стрелки, как показано на рис. 6.6, и аргумент принимается отрицательным.

Таким образом, формулы для определения аргумента в различных четвертях имеют следующий вид:

1 четверть: 2 четверть:

(6.13)

3 четверть: 4 четверть:

(6.14)

Отсюда следует, что выражение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива в некотором своем диапазоне частот. Граничные частоты диапазонов определяют по знаку действительных и мнимых частей числителя и знаменателя комплексной передаточной функции.

Для построения АФХ (годографа) целесообразно воспользоваться не показательной формой комплексного параметра T(jω) = T(ω)e^jφ(ω), а алгебраической формой T(jω) = A(ω) + jB(ω) = T(ω)cosφ(ω) + jT(ω)sinφ(ω). Это объясняется тем, что годограф проще построить в декартовой системе координат, а не в полярных координатах. Таким образом, формулы координат годографа легко получаются в результате расчеты АЧХ и ФЧХ

A

(ω) = T(ω)cosφ(ω); B(ω) = T(ω)sinφ(ω). (6.15)

Пример 6.4. Получить аналитические выражения АЧХ, ФЧХ и АФХ коэффициента передачи (6.10) цепи в примере 6.2.

Решение.

Проведем замену p = jω и выделим действительные и мнимые части в числителе и знаменателе

(6.16)

Модуль коэффициента передачи т.е формула АЧХ имеет вид

(6.17)

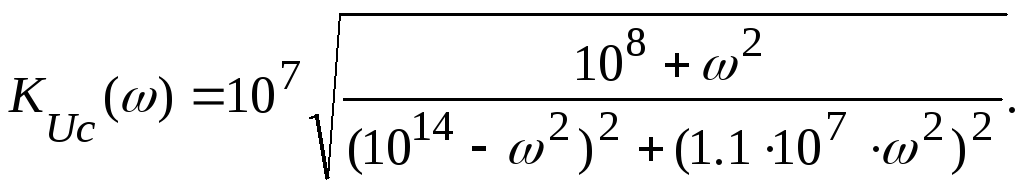
Для получения выражения ФЧХ по формуле φ(ω) = φ_числ(ω) – φ_знам(ω) проведем анализ числителя и знаменателя выражения комплексного коэффициента передачи (6.16). Числитель M(j) = (10⁴ + j) является комплексным числом с положительными действительной и мнимой частями во всем частотном диапазоне. Поэтому применяем формулу аргумента для первой четверти

Мнимая часть знаменателя D(ω) = 1.110⁷ω положительная при любых значениях частоты. Знак действительной части C(ω) = (10¹⁴ – ω²) меняется при изменении частоты.

При определенной частоте ω = ω₀ действительная часть может быть равна нулю C(ω₀) = (10¹⁴ – ω₀²) = 0. Эта частота равна ω₀ = 10⁷. Аргумент знаменателя на этой частоте равен

На частотах ω < 10⁷ действительная часть знаменателя C(ω) > 0. Поэтому φ_знам(ω) нужно рассчитывать по формуле (6.13) для первой четверти

На частотах ω > 10⁷ действительная часть знаменателя C(ω) < 0 . Поэтому φ_знам(ω) нужно рассчитывать по формуле (6.13) для второй четверти

Таким образом, ФЧХ коэффициента передачи в данном примере будет описываться различными формулами для следующих частотных областях

1

) ω < 10⁷

2) ω = ω₀ =10⁷

(6.18)

3) ω > 10⁷

Амплитудно-фазовую характеристику (годограф) удобнее строить в декартовой системе координат на комплексной плоскости K(jf) = A(f) + jB(f). Для этого нужно провести расчет по формулам 6.19

A() = K()cosφ(); B() = K()sinφ(). (6.19)