
- •Елементи теорії ймовірностей
- •§1. Означення ймовірності
- •Простіші властивості ймовірності
- •Класичне означення ймовірності
- •VII. Геометрична ймовірність.
- •VIII. Умовна ймовірність. Формула Байєса.
- •§2. Послідовності незалежних випробувань
- •I. Послідовність незалежних випробувань.
- •II. Схема Бернуллі
- •Iіi. Граничні теореми у схемі Бернуллі
- •§3. Випадкові величини
- •II. Дискретна випадкова величина
- •III. Неперервна випадкова величина
- •§4. Нормальний розподіл та його властивості
- •§5. Кореляція
- •V. Кореляційний момент:
- •Vі. Коефіцієнт кореляції
- •Vіі. Лінійна регресія -
- •Елементи математичної статистики
- •§1 Вибірка та її характеристики
- •Варіаційний ряд.
- •Емпірична (вибіркова) функція розподілу
- •Полігон частот
- •Гістограма
- •§2 Задача перевірки статистичних гіпотез
- •Гіпотеза про параметри нормального розподілу : .
- •Гіпотеза про параметри нормального розподілу : .
- •Гіпотеза про закон розподілу. Критерій Колмогорова.
- •§3. Довірчі інтервали
- •§4. Вибіркова кореляція
- •§5. Значущість вибіркового коефіцієнту кореляції
- •§6. Критерій , як критерій незалежності ознак
§5. Кореляція
І. Випадковий вектор
Вектор
![]() ,
де
,
де![]() - випадкові величини, називається
випадковим
вектором.
- випадкові величини, називається
випадковим
вектором.
ІІ. Закон розподілу дискретного двовимірного випадкового вектору
Припустимо, що дві дискретні випадкові величини приймають наступні значення:
![]()
![]()
Сумісний закон розподілу двох величин (двовимірного випадкового вектору):
![]() .
.
Задається або таблицею:
|
|
|
Σ |
||
|
|
… |
|
||
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
|
|
|
… |
|
|
|
Σ |
|
… |
|
1 |
де сума
по рядках:
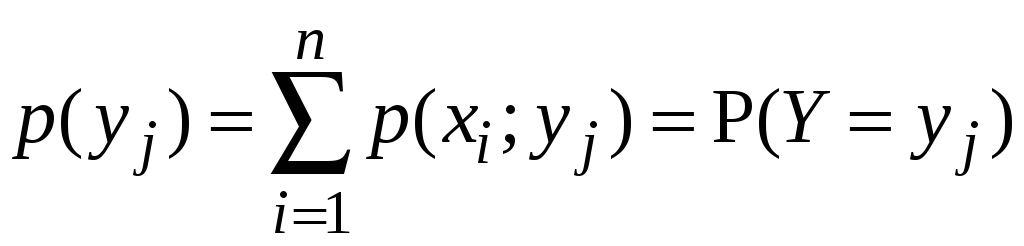 - закон розподілу
- закон розподілу
![]() ,
,
сума по
стовпчиках:
 - закон розподілу
- закон розподілу
![]() ,
,
або формулою.
ІІІ. Умовний закон розподілу:
![]() :
: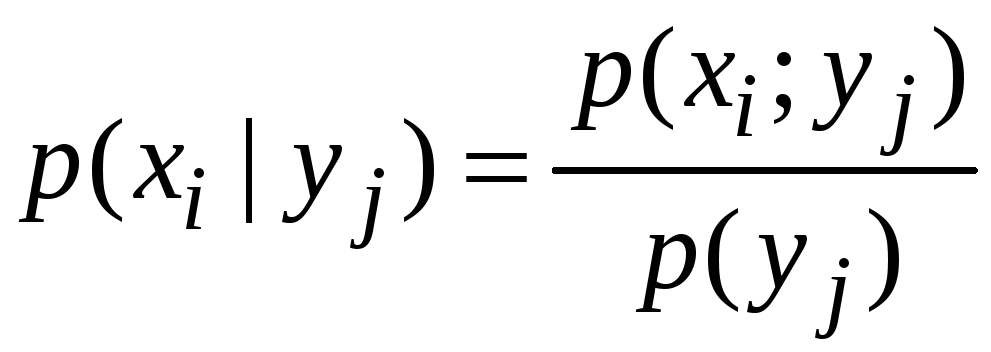 .
.
![]() :
: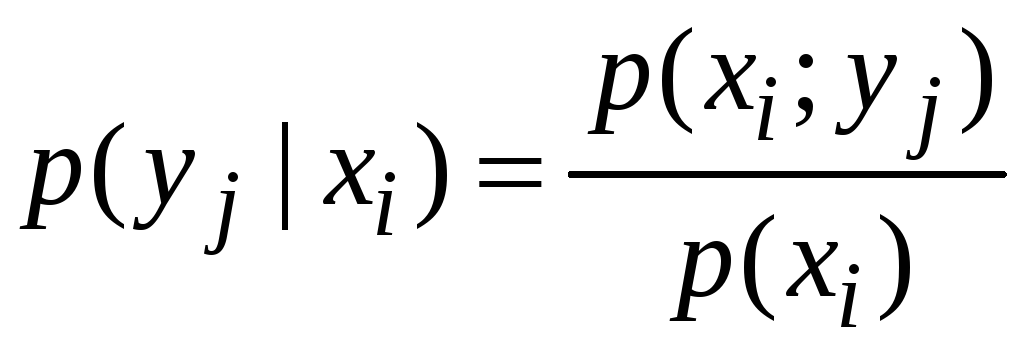 .
.
Випадкові
величини
![]() та
та
![]() незалежні,
якщо умовні закони розподілу співпадають
з безумовними:
незалежні,
якщо умовні закони розподілу співпадають
з безумовними:
![]() ,
,
![]() .
.
ІV. Умовне математичне сподівання. Регресія
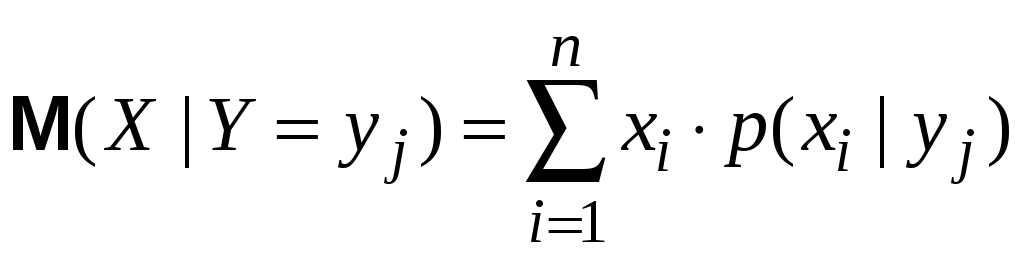
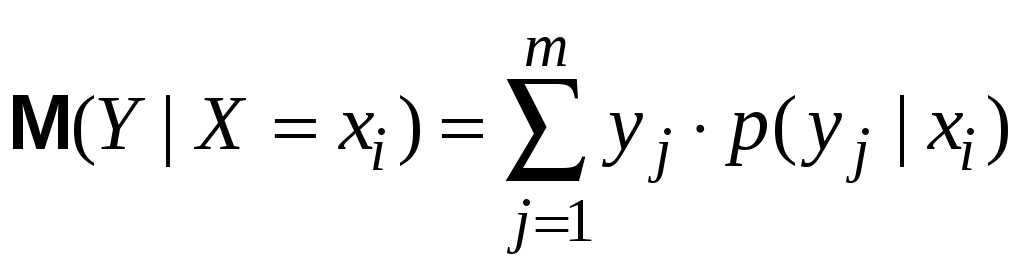
Як бачимо, умовне мат. сподівання однієї величини є функцією від значень другої величини. Ця функція називається регресією.
Функція
регресії
![]() на
на
![]() :
:
![]()
Функція
регресії
![]() на
на
![]() :
:
![]()
V. Кореляційний момент:
![]()
Обчислення
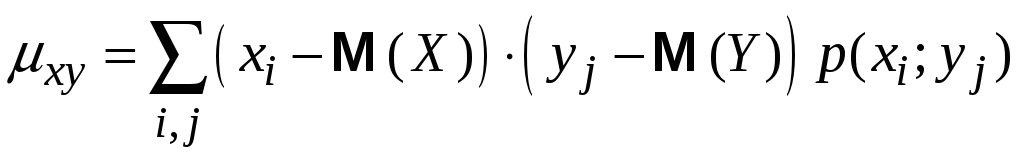
Легко показати, що
![]()
Обчислення
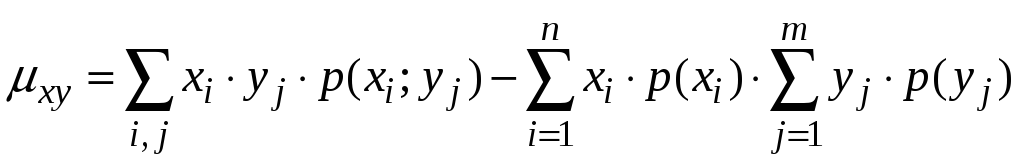
Якщо
величини
![]() та
та
![]() незалежні, кореляційний момент дорівнює
нулю.
незалежні, кореляційний момент дорівнює
нулю.
Vі. Коефіцієнт кореляції

де
![]() ,
,
![]() - середні квадратичні відхилення величин
- середні квадратичні відхилення величин
![]() та
та
![]() .
.
Величини
![]() та
та
![]() корельовані,
якщо
корельовані,
якщо
![]() .
.
Величини
![]() та
та
![]() некорельовані,
якщо
некорельовані,
якщо
![]() .
.
Якщо величини корельовані, то вони залежні, некорельовані величини можуть бути як залежними, так і незалежними.
Зауваження. Коефіцієнт кореляції не може бути по модулю більше одиниці.
![]()
Vіі. Лінійна регресія -
- лінійне наближення до функції регресії.
Лінійна
регресія
![]() на
на
![]() :
функція регресії
:
функція регресії
![]() замінюється лінійною функцією регресії
замінюється лінійною функцією регресії
![]() .
.
Коефіцієнт
регресії
![]() на
на
![]()
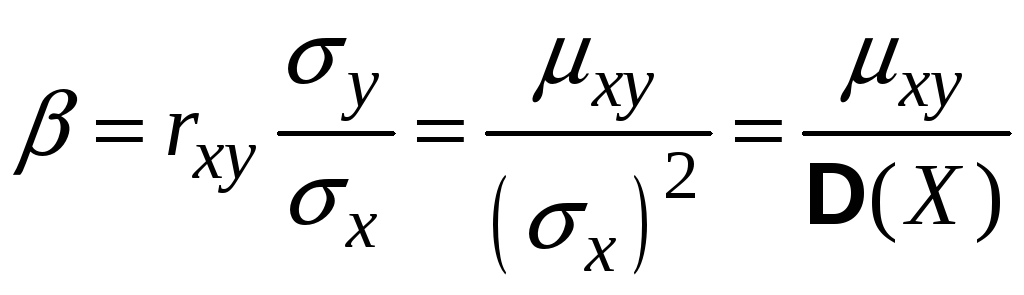
Лінійна
функція регресії
![]() на
на
![]() :
:
![]()
Пряма з рівнянням
![]()
називається
прямою
лінійної регресії
![]() на
на
![]() .
.
Найбільш
імовірна помилка, що виникає під час
заміни регресії на лінійну регресію
оцінюється через залишкове
відхилення
![]() відносно
відносно
![]()
![]() .
.
Лінійна
регресія
![]() на
на
![]() :
функція регресії
:
функція регресії
![]() замінюється лінійною функцією регресії
замінюється лінійною функцією регресії
![]() .
.
Коефіцієнт
регресії
![]() на
на
![]()
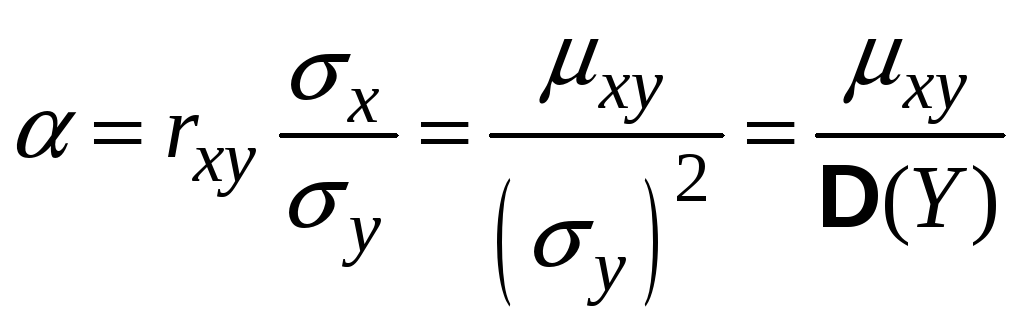
Лінійна
функція регресії
![]() на
на
![]()
![]()
Пряма з рівнянням
![]()
називається
прямою
лінійної регресії
![]() на
на
![]() .
.
Найбільш
імовірна помилка, що виникає під час
заміни регресії на лінійну регресію
оцінюється через залишкове
відхилення
![]() відносно
відносно
![]()
![]() .
.
Точка
перетину прямих регресії з координатами
![]() називається центром
сумісного розподілу
називається центром
сумісного розподілу
![]() та
та
![]() .
.
Приклад.
Задано
таблицею сумісний розподіл випадкових
величин
![]() та
та
![]() .
Знайти
розподіли
.
Знайти
розподіли
![]() та
та
![]() ,
регресію та лінійну регресію
,
регресію та лінійну регресію
![]() на
на
![]() та
та
![]() на
на
![]() .
.
|
|
|
Σ |
||
|
|
|
|
||
|
|
0,10 |
0,30 |
0,20 |
0,60 |
|
|
0,06 |
0,18 |
0,16 |
0,40 |
|
Σ |
0,16 |
0,48 |
0,36 |
1 |
Знайдемо
суми по рядках та по стовпчиках. Отримаємо
закони розподілу випадкових величин
![]() та
та
![]() .
.
|
|
|
|
|
|
|
0,16 |
0,48 |
0,36 |
|
|
|
|
|
|
0,60 |
0,40 |
Знайдемо умовні закони розподілу.
![]() :
: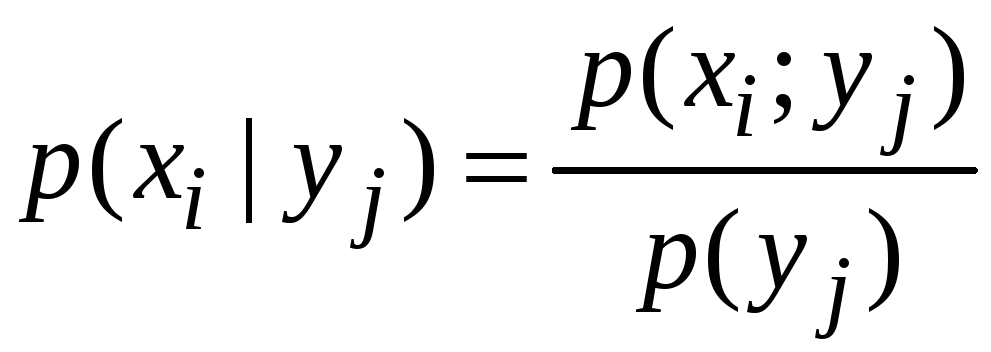 .
.
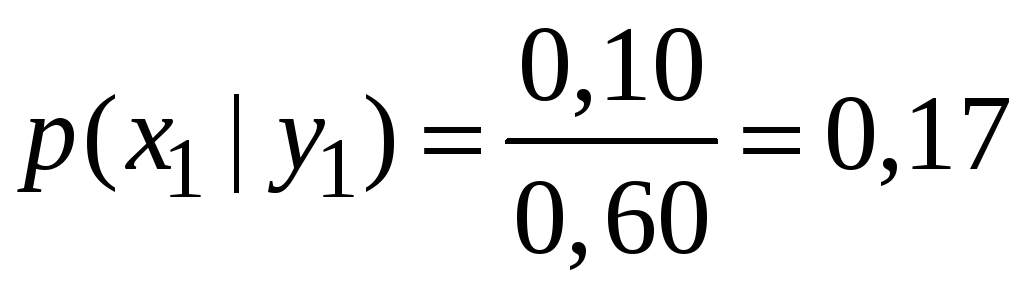
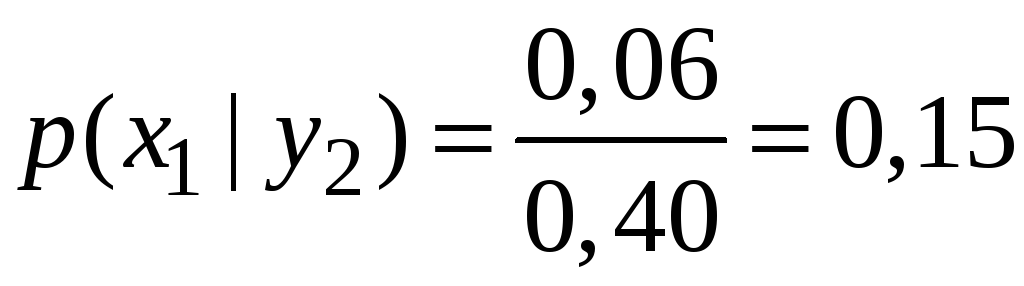
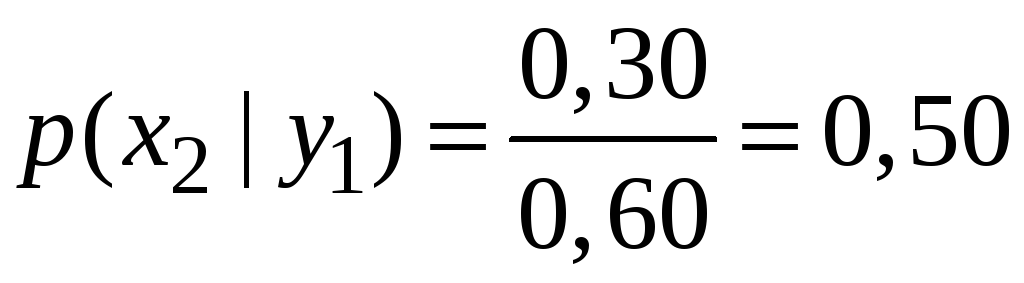
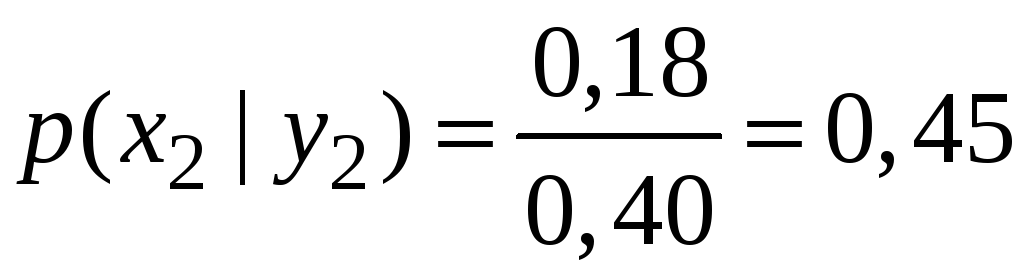
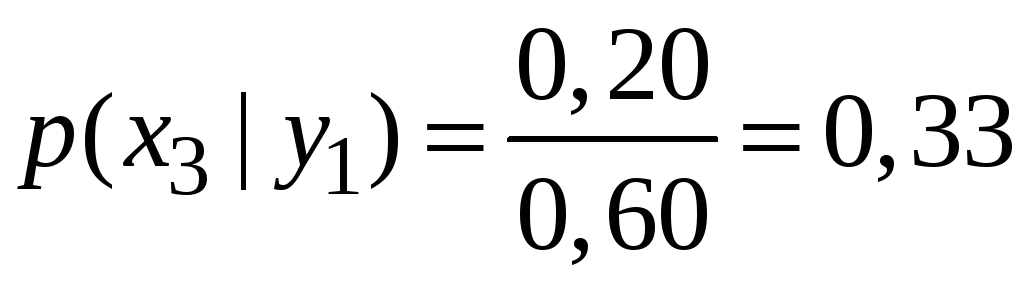
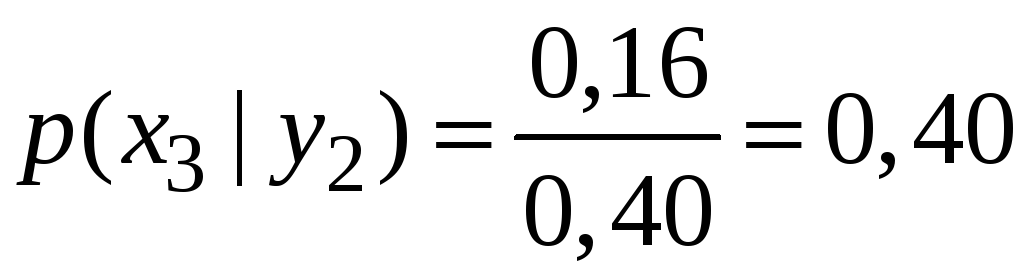
![]() :
: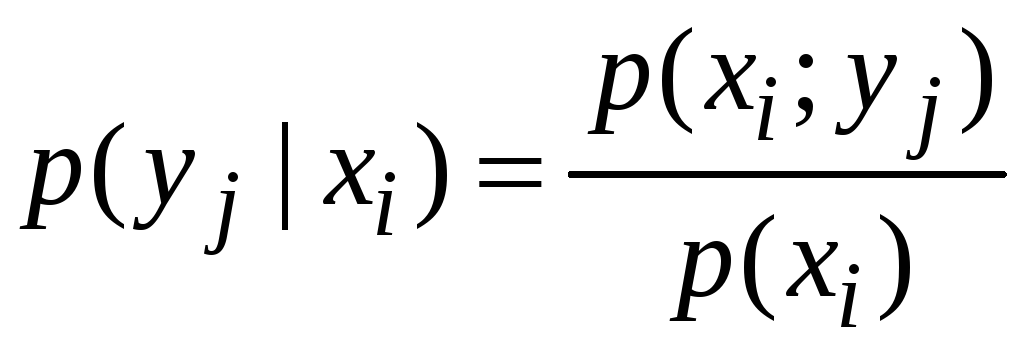 .
.
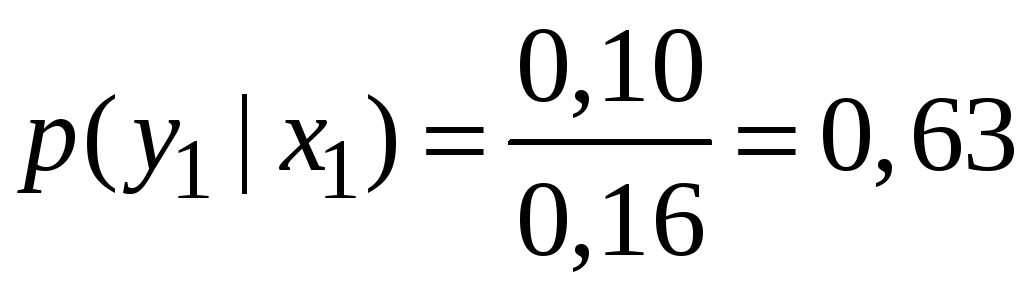
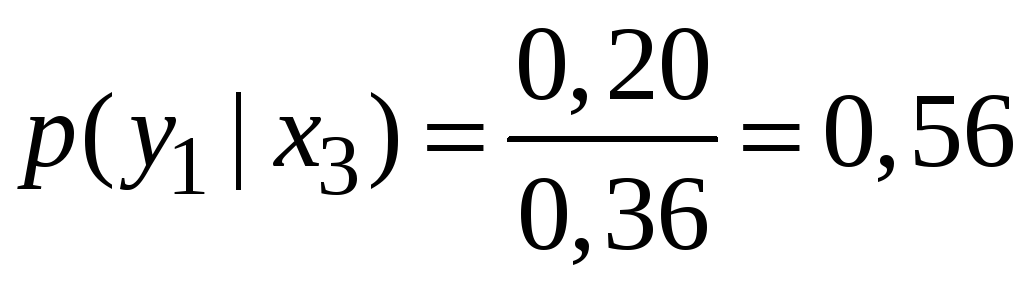
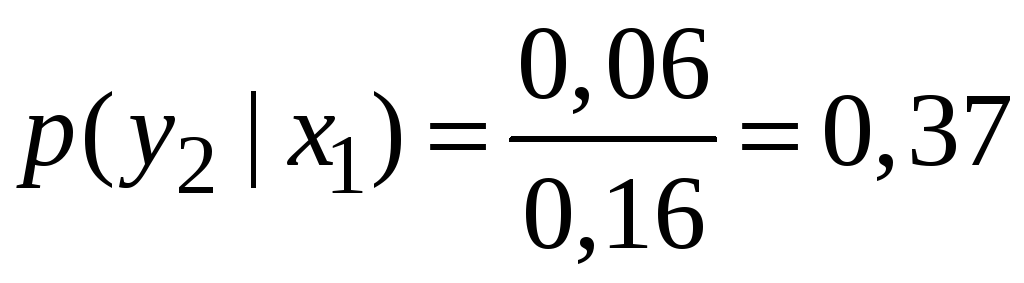
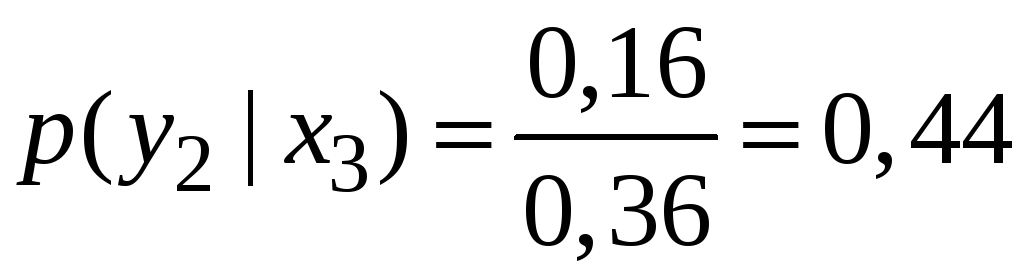
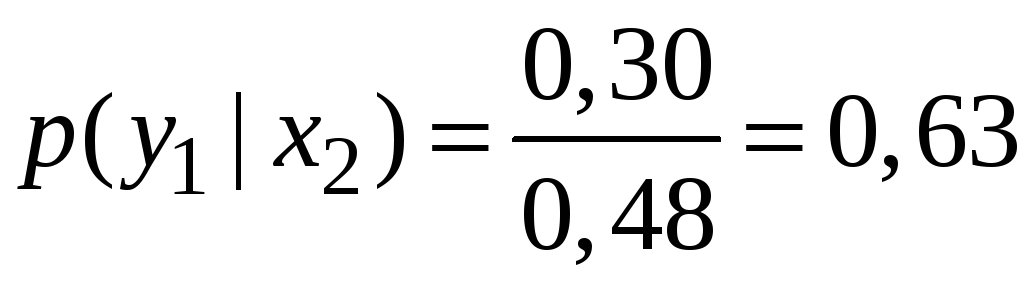
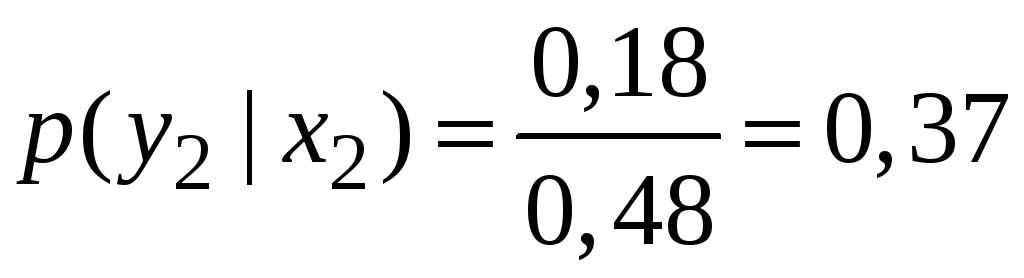
Умовні мат. сподівання.
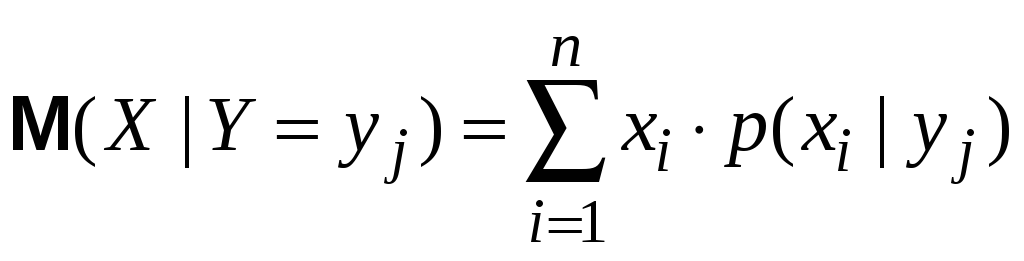
![]()
![]()
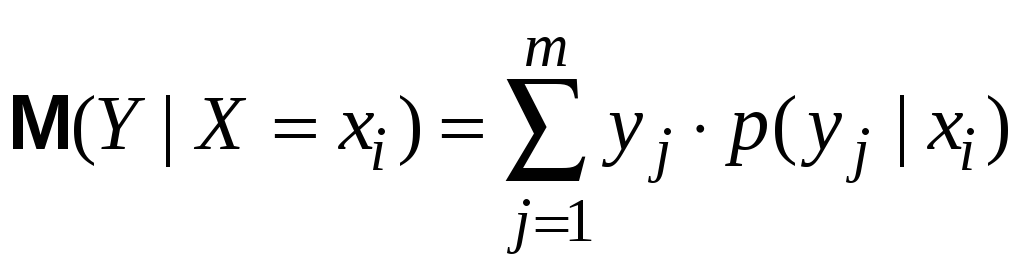
![]()
![]()
![]()
Знайдені
сукупності чисел складають відповідно
регресії
![]() на
на
![]() та
та
![]() на
на
![]() .
.
Знайдемо
лінійні регресії
![]() на
на
![]() та
та
![]() на
на
![]() .
.
Обчислимо
за законами розподілу мат. сподівання
та дисперсії
![]() та
та
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Обчислимо
мат. сподівання добутку величин
![]() та
та
![]() :
:
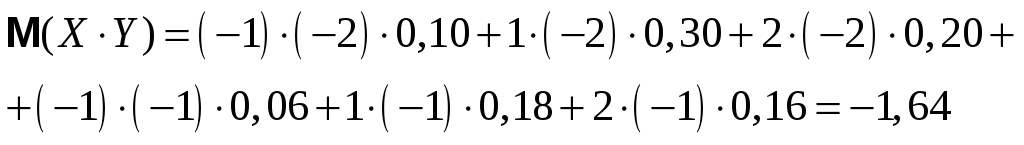
Обчислимо кореляційний момент
![]()
Коефіцієнт кореляції
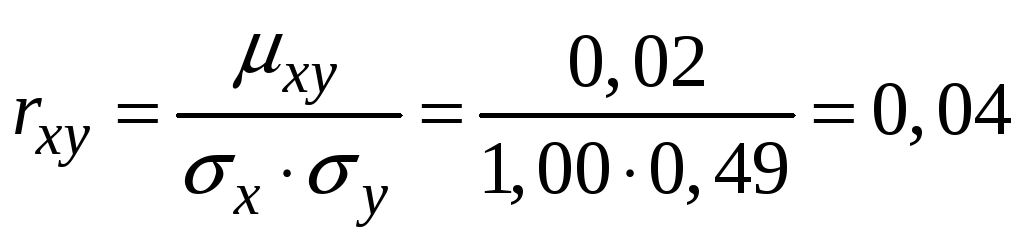
Коефіцієнти регресії
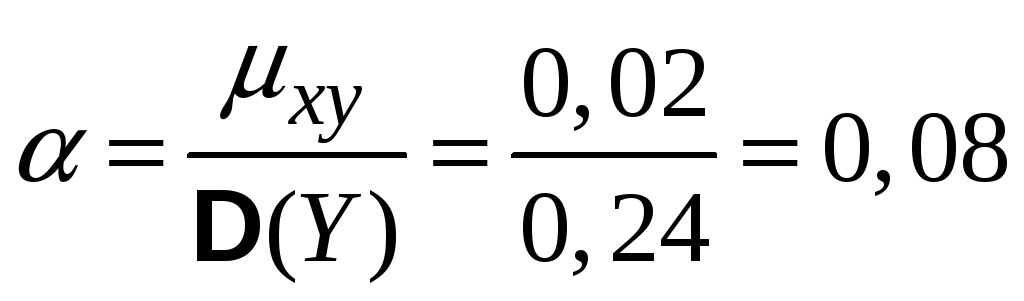
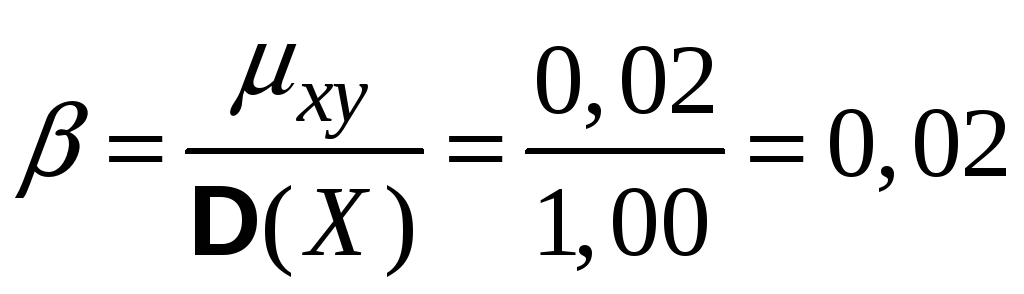
Лінійна
регресія
![]() на
на
![]()
![]()
![]()
Пряма
регресії
![]() на
на
![]()
![]()
або
![]()
Залишкове
відхилення
![]() відносно
відносно
![]()
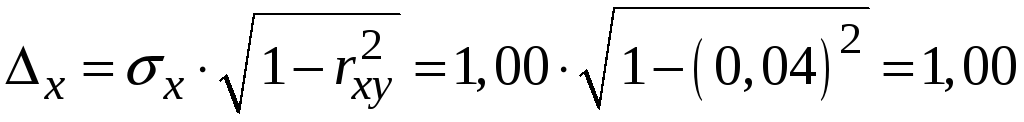
Лінійна
регресія
![]() на
на
![]()
![]()
![]()
Пряма
регресії
![]() на
на
![]()
![]()
або
![]()
Залишкове
відхилення
![]() відносно
відносно
![]()
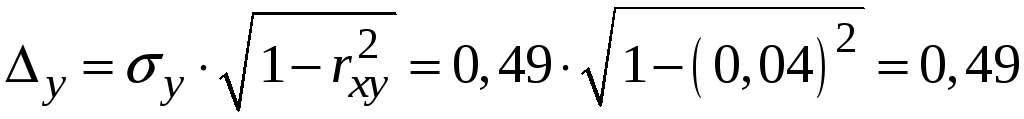 .
.
Центр
сумісного розподілу![]() та
та
![]() :
:
![]() .
.
Порівняємо значення функцій регресії та наближених функцій лінійної регресії:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Як бачимо, отримані значення дуже добре узгоджуються між собою.
Зауваження. Аналогічні співвідношення існують і для неперервних випадкових величин (див., наприклад, [1]).
