
- •Елементи теорії ймовірностей
- •§1. Означення ймовірності
- •Простіші властивості ймовірності
- •Класичне означення ймовірності
- •VII. Геометрична ймовірність.
- •VIII. Умовна ймовірність. Формула Байєса.
- •§2. Послідовності незалежних випробувань
- •I. Послідовність незалежних випробувань.
- •II. Схема Бернуллі
- •Iіi. Граничні теореми у схемі Бернуллі
- •§3. Випадкові величини
- •II. Дискретна випадкова величина
- •III. Неперервна випадкова величина
- •§4. Нормальний розподіл та його властивості
- •§5. Кореляція
- •V. Кореляційний момент:
- •Vі. Коефіцієнт кореляції
- •Vіі. Лінійна регресія -
- •Елементи математичної статистики
- •§1 Вибірка та її характеристики
- •Варіаційний ряд.
- •Емпірична (вибіркова) функція розподілу
- •Полігон частот
- •Гістограма
- •§2 Задача перевірки статистичних гіпотез
- •Гіпотеза про параметри нормального розподілу : .
- •Гіпотеза про параметри нормального розподілу : .
- •Гіпотеза про закон розподілу. Критерій Колмогорова.
- •§3. Довірчі інтервали
- •§4. Вибіркова кореляція
- •§5. Значущість вибіркового коефіцієнту кореляції
- •§6. Критерій , як критерій незалежності ознак
Iіi. Граничні теореми у схемі Бернуллі
Обчислення
за формулою (3) значно ускладнюються,
коли кількість випробувань
![]() є великим. Також важко підсумовувати
ймовірності виду (3). Наприклад, для
знаходження ймовірності потрапляння
кількості успіхів у певний проміжок
треба додавати вирази типу (3) для всіх
значень
є великим. Також важко підсумовувати
ймовірності виду (3). Наприклад, для
знаходження ймовірності потрапляння
кількості успіхів у певний проміжок
треба додавати вирази типу (3) для всіх
значень
![]() з цього проміжку:
з цього проміжку:

Ускладнення
виникають також під час обчислень з
малими
![]() або
або
![]() .
В усіх цих випадках можуть допомогти
так звані граничні
теореми,
які містять асимптотичні формули при
.
В усіх цих випадках можуть допомогти
так звані граничні
теореми,
які містять асимптотичні формули при
![]() .
.
Теорема
Пуассона. Якщо
ймовірність
![]() коли
коли
![]() так,
що
так,
що
![]() ,
то
,
то
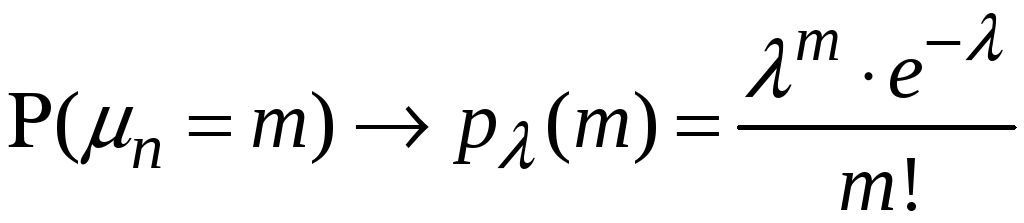
при
будь-якому сталому
![]() ,
,
![]() .
.
Доведення.
Позначимо
![]() .
Тоді
.
Тоді
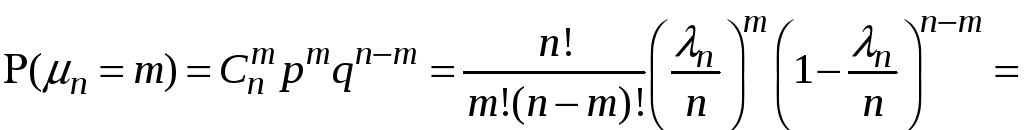
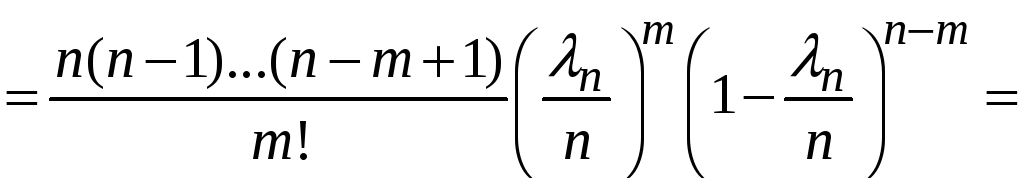
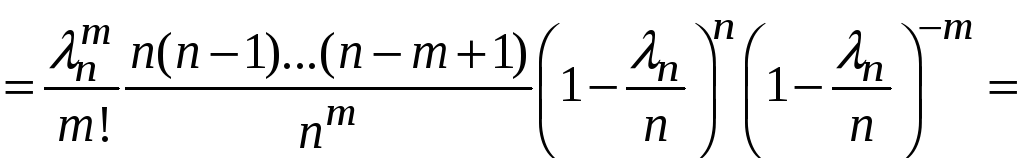
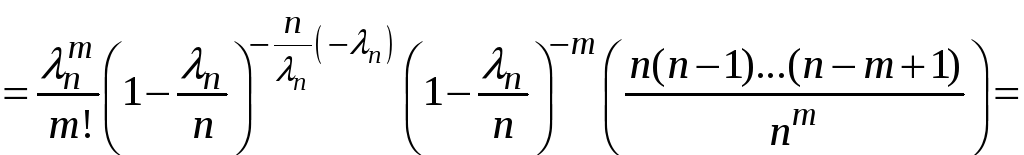
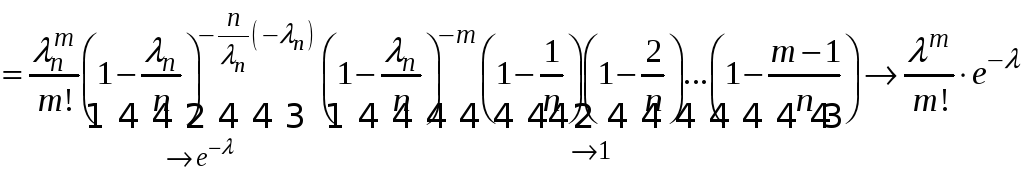 коли
коли
![]() ,
оскільки за умови теореми
,
оскільки за умови теореми
![]() .
Теорему доведено.
.
Теорему доведено.
З
теореми випливає, що для великих
![]() та малих
та малих
![]() можна користуватися наближеною
формулою
можна користуватися наближеною
формулою
![]() ,
(4)
,
(4)
де
![]() ,
а
,
а
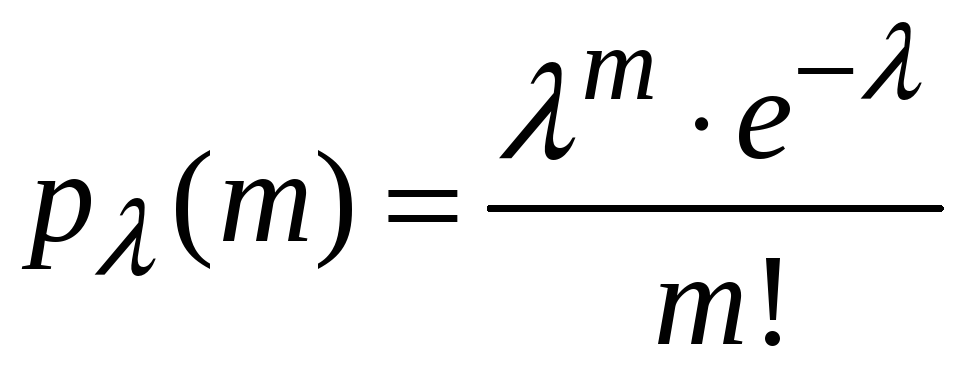 .
.
Зауваження.
Числа
![]() при деяких значеннях параметрів
при деяких значеннях параметрів
![]() та
та
![]() ,
важливих для застосувань, можна знайти
по таблицях (див. Додаток). Набір вказаних
чисел складає так званий розподіл
Пуассона (див.
§3,
п.ІІ, пр.2).
,
важливих для застосувань, можна знайти
по таблицях (див. Додаток). Набір вказаних
чисел складає так званий розподіл
Пуассона (див.
§3,
п.ІІ, пр.2).
Помилку наближеної формули Пуассона можна оцінити, як
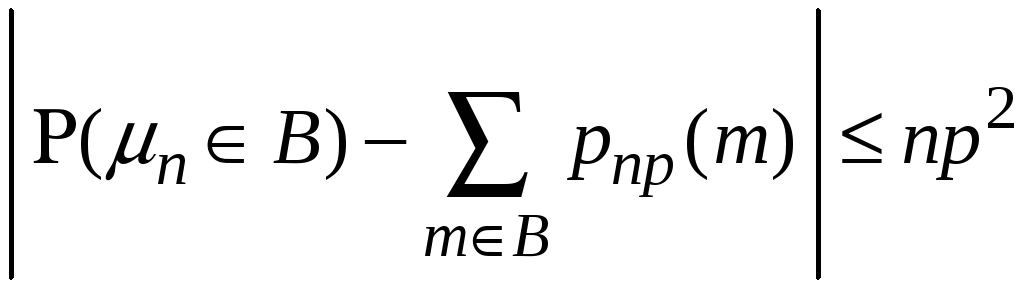 .
.
Тут В – це довільний набір з чисел 0, 1, 2, … .
Якщо
малим буде значення
![]() (тобто для великих
(тобто для великих
![]() ),
то формулою можна користуватися для
наближеного обчислення кількості
невдач.
),
то формулою можна користуватися для
наближеного обчислення кількості
невдач.
Коли
обидва параметри
![]() та
та
![]() помітно відрізняються від нуля, можна
користуватися теоремами Муавра-Лапласа.
Розглянемо функцію Лапласа (інтеграл
імовірності). Позначимо
помітно відрізняються від нуля, можна
користуватися теоремами Муавра-Лапласа.
Розглянемо функцію Лапласа (інтеграл
імовірності). Позначимо
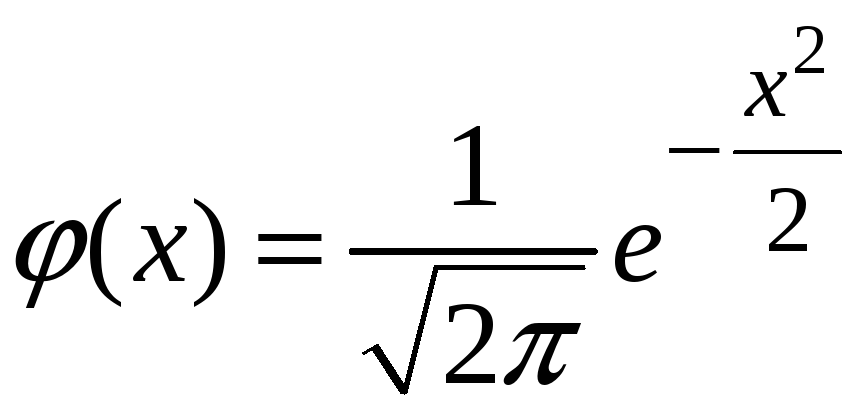 ,
,
 .
.
(Значення
функції
Лапласа
![]() можна знайти по таблицях, див. Додаток.)
можна знайти по таблицях, див. Додаток.)
Зауваження.
Іноді
замість
![]() розглядають функцію Лапласа у вигляді
розглядають функцію Лапласа у вигляді
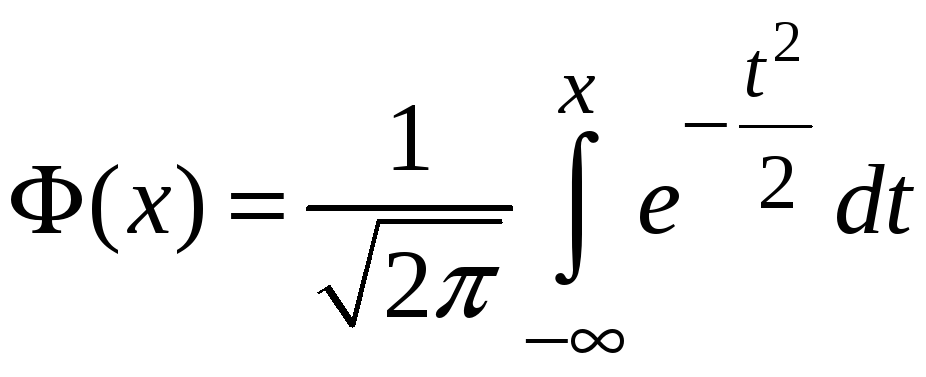 .
.
Її значення також можна знайти по таблицях, (див. Додаток). Функції пов’язані співвідношенням
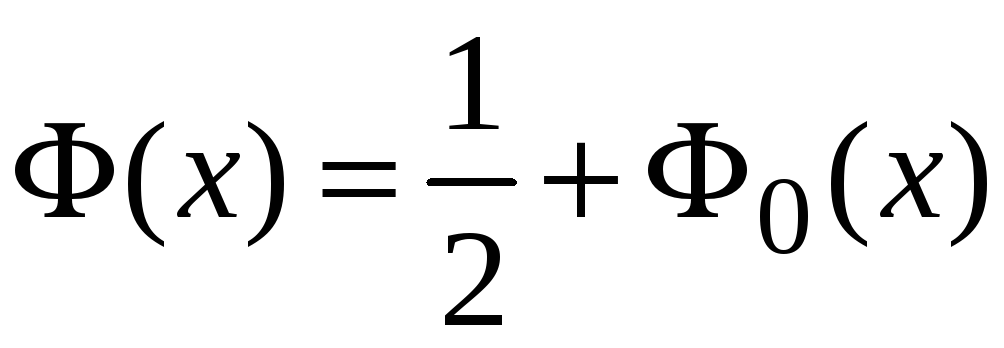 .
.
В англомовних книжках розглядається так звана функція помилки (error function) у вигляді
 .
.
Вона
пов’язана з
![]() співвідношенням
співвідношенням
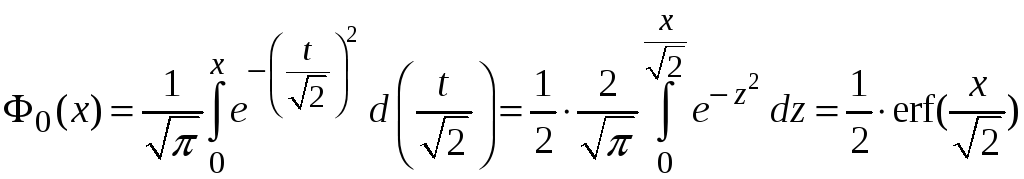 .
.
Властивості функції Лапласа.
1)
 ,
причому для застосувань значення
приймаються рівними 0,5 вже починаючи з
,
причому для застосувань значення
приймаються рівними 0,5 вже починаючи з
![]() .
.
2) Функція
Лапласа є непарною, тобто
![]() .
Це допомагає обчислювати значення
функції для від’ємних аргументів.
.
Це допомагає обчислювати значення
функції для від’ємних аргументів.
Локальна
теорема Муавра-Лапласа. Якщо
ймовірність
![]() ,
,
![]() ,
є сталою, величина
,
є сталою, величина
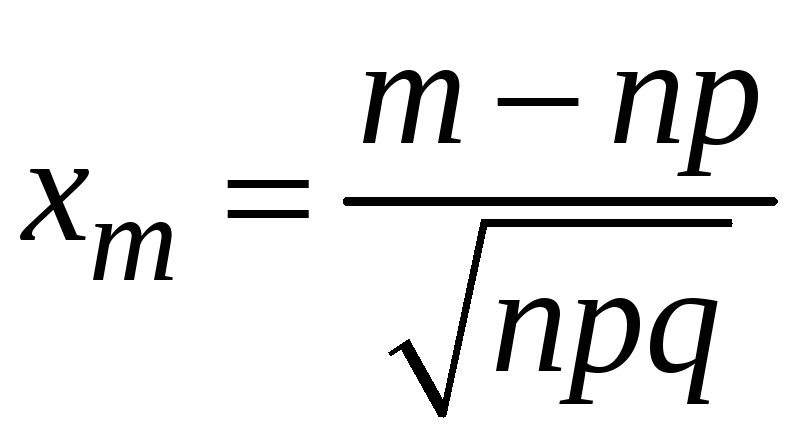
є
рівномірно обмеженою по
![]() та
та
![]() :
:
![]() ,
,
то справджується асимптотична рівність
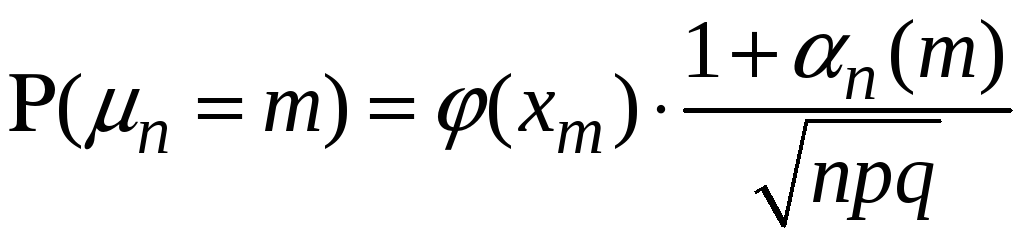 ,
,
коли
![]() ,
де нескінченно мала
,
де нескінченно мала
![]() задовольняє нерівність
задовольняє нерівність
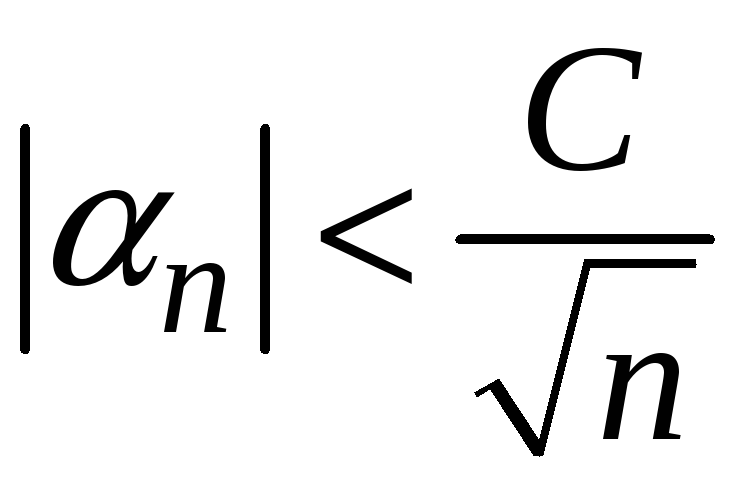 ,
де С
> 0
– стала
величина.
,
де С
> 0
– стала
величина.
З теореми випливає наближена рівність
 ,
(5)
,
(5)
яка дає
непогане наближення для випадку, коли
![]() .
Крім
.
Крім
того,
![]() та
та
![]() не
повинні значно відрізнятися одне від
одного, наприклад, для
не
повинні значно відрізнятися одне від
одного, наприклад, для
![]() наближення
буде дуже поганим.
наближення
буде дуже поганим.
Інтегральна
теорема Муавра-Лапласа. Якщо
ймовірність
![]() ,
,
![]() ,
є сталою, то при
,
є сталою, то при
![]() ,
,
 ,
,
рівномірно
по
![]() та
та
![]() (
(![]() ).
).
З теореми випливає наближена рівність
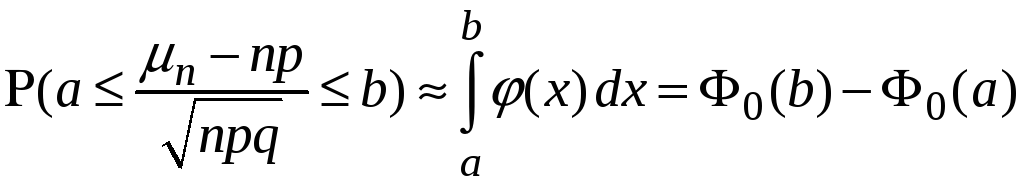 ,
,
яка
також дає непогане наближення для
випадку, коли
![]() .
.
За допомогою заміни змінних попередня формула легко перетворюється на:
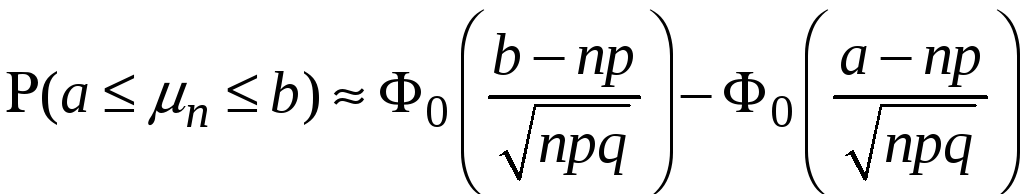 .
(6)
.
(6)
Приклади. 1) Передається повідомлення з 500 знаків. Імовірність помилки під час передачі кожного знаку дорівнює 0,01. Вважаючи, що спотворення знаків виникає незалежно від попередніх, знайти ймовірність того, що:
а) у повідомленні буде не більше 2 помилок,
б) у повідомленні буде не менше 3 помилок.
Розв’язання.
Маємо
![]()
а) Треба обчислити ймовірність
![]()
Оскільки
![]() велике, а
велике, а
![]() мале, можна застосувати формулу Пуассона
(4):
мале, можна застосувати формулу Пуассона
(4):
![]() ,
,
![]() ,
,
![]() .
.
За таблицею розподілу Пуассона (див. Додаток),
![]() ,
,
![]() ,
,
![]() .
.
Звідси
![]() .
.
б)
Помітимо, що подія «не менше 3 помилок»
(![]() )
протилежна події «не більше 2 помилок»
(
)
протилежна події «не більше 2 помилок»
(![]() ),
яка розглядалася у п.а). Тому
),
яка розглядалася у п.а). Тому
![]()
2) Монету підкидають 1600 разів.
а) Знайти ймовірність того, що герб випаде рівно 800 разів.
Розв’язання.
Маємо
![]()
Бачимо,
що
![]() ,
можливо застосувати локальну формулу
Муавра-Лапласа (5).
,
можливо застосувати локальну формулу
Муавра-Лапласа (5).
Треба
обчислити ймовірність
![]() ,
тобто
,
тобто
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
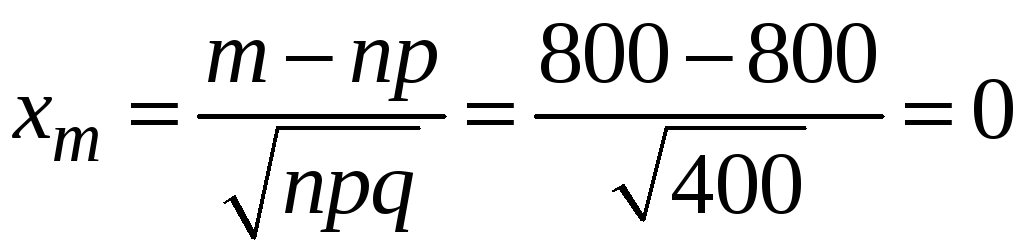 .
Звідси
.
Звідси
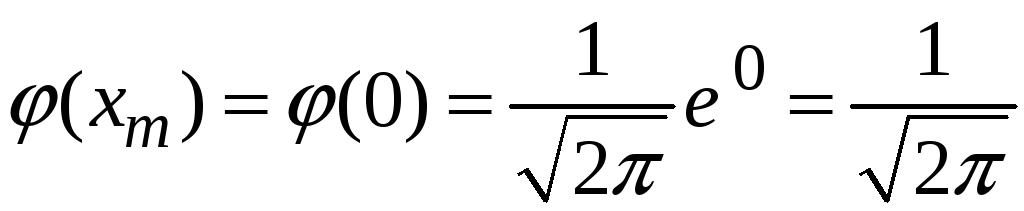
Тому
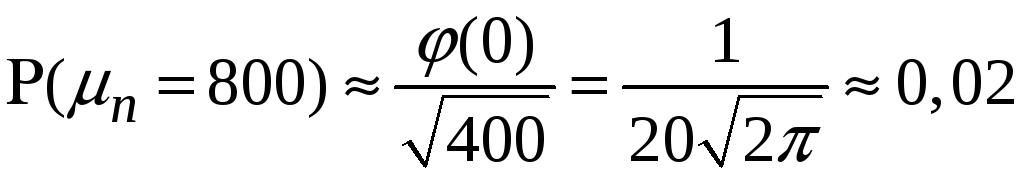 .
.
б) Знайти ймовірність того, що герб випаде не менше ніж 750 та не більше ніж 850 разів.
Розв’язання.
Оскільки
![]() ,
можливо застосувати інтегральну формулу
Муавра-Лапласа (6).
,
можливо застосувати інтегральну формулу
Муавра-Лапласа (6).
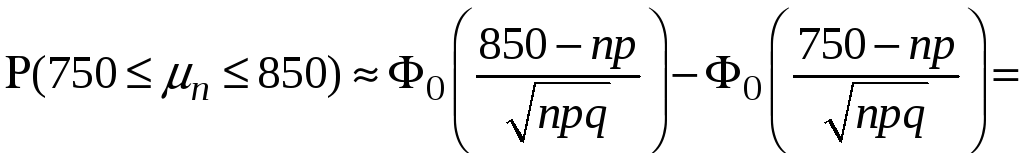
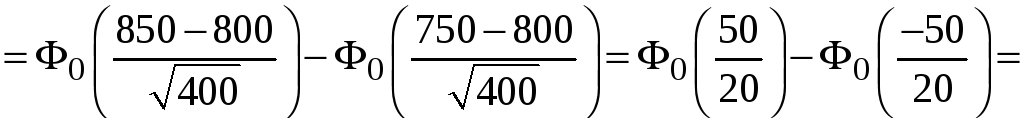
![]()
за
непарністю функції Лапласа. За таблицею
значень функції Лапласа (див. Додаток),
![]() ,
тому
,
тому
![]() .
.
Як бачимо, ймовірність отримати конкретне значення у цьому випадку є дуже малою, а ймовірність отримати будь-яке значення з певного інтервалу, що охоплює це конкретне значення – дуже великою.
