§2. Послідовності незалежних випробувань
I. Послідовність незалежних випробувань.
Послідовністю незалежних випробувань називається математична модель серії експериментів, що повторюються у однакових умовах.
Припустимо,
що проводиться серія з
експериментів, в кожному з яких можливі
несумісних результатів, причому
результати попередніх експериментів
не впливають на результат поточного.
Можна ототожнювати результат експерименту
з його номером, тобто вважати, що у
-тому
експерименті з’являється результат
,
який приймає одне з
значень:
Ймовірність
результату
позначимо через
,
де
.
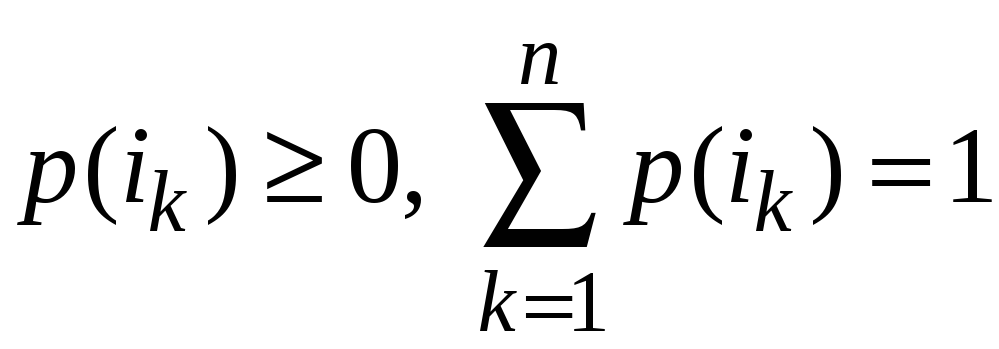Елементарною подією вважатимемо ланцюжок послідовних результатів певної серії експериментів
.
Тоді простір елементарних подій
.
Оскільки результати експериментів вважаються незалежними, то за означенням незалежності ймовірність результату серії експериментів дорівнює добутку ймовірностей результатів експериментів, які складають серію, тобто
.
(1)
Тоді на
алгебрі всіх підмножин простору
можна однозначно визначити ймовірність
випадкової події
:
.
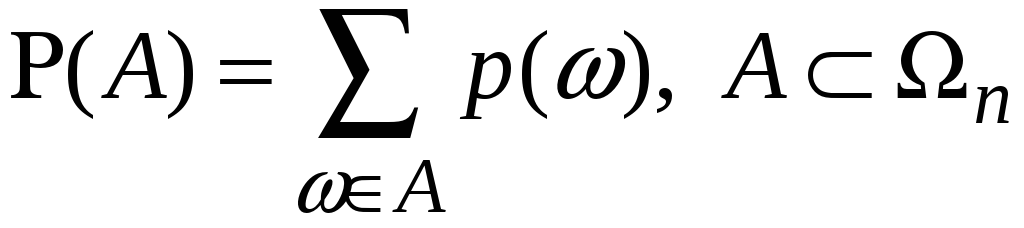(2)
Легко
показати, що
,
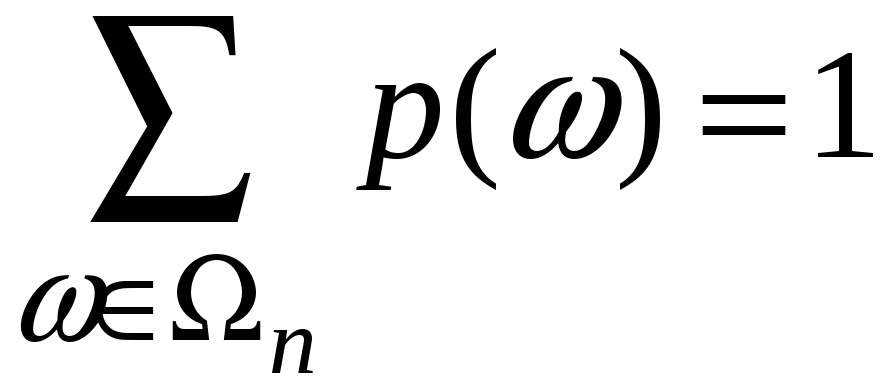тобто вказана функція
дійсно є ймовірністю. Побудована
імовірнісна модель називається
послідовністю
незалежних випробувань або
поліноміальною
схемою.
II. Схема Бернуллі
Схемою
Бернуллі називають
частинний випадок поліноміальної схеми,
коли
.
Два можливі результати кожного
випробування Бернуллі інтерпретуються,
як «успіх» або «невдача» та позначаються
зазвичай 1 чи 0 відповідно. Ймовірність
успіху позначається літерою
,
ймовірність невдачі -
.
Зрозуміло, що
.
Елементарною подією у схемі Бернуллі
буде ланцюжок з
одиниць та нулів:
наприклад. Позначимо через
кількість
успіхів у
перших випробуваннях Бернуллі.
Наприклад,
.
Зазвичай
у схемі Бернуллі шукають імовірність
отримати певну кількість (
)
успіхів у послідовності в
випробувань, тобто ймовірність події
,
що складається з всіх ланцюжків, які
містять рівно
одиниць та
нулів (на різних місцях, зрозуміло).
Зауваження. «Успіхом» у схемі Бернуллі вважається результат, що нас цікавить, незалежно від його приємності чи неприємності. Якщо досліджується, наприклад, імовірність захворіти на грип під час епідемії, то «успіхом» вважається наявність захворювання, незважаючи на неприємність цієї події.
Теорема
Бернуллі. Якщо
- кількість успіхів у
випробуваннях Бернуллі, то
,
(3)
де
,
- імовірність успіху в окремому
випробуванні.
Доведення.
За
формулою (1), де
,
причому одиниць рівно
та рівно
нулів, маємо, що кожен ланцюжок, що нас
цікавить, має однакову ймовірність
.
Ланцюжки відрізняються тільки розміщенням
одиниць серед нулів. Різних способів
розмістити
одиниць на
місцях буде рівно
.
Таким чином, наша подія складається з
ланцюжків
,
що мають однакову ймовірність
.
За означенням (2) імовірність події
дорівнює сумі ймовірностей всіх таких
ланцюжків, тобто добутку
.
Теорему доведено.
Зауваження. За формулою бінома Ньютона
.
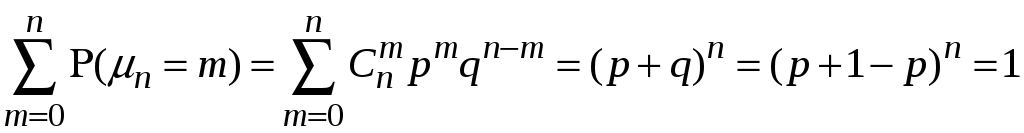Приклад. Передається повідомлення з 5 знаків. Імовірність помилки під час передачі кожного знаку дорівнює 0,01. Вважаючи, що спотворення знаків виникає незалежно від попередніх, знайти ймовірність того, що:
а) повідомлення буде передано без спотворень,
б) у повідомленні буде рівно 1 помилка,
в) у повідомленні буде не менше 2 помилок.
Розв’язання.
Маємо
(Передачу кожного знака вважаємо
незалежним випробуванням, успіхом
вважаємо появу помилки.)
а) В
даному випадку
.
За формулою (3):
.
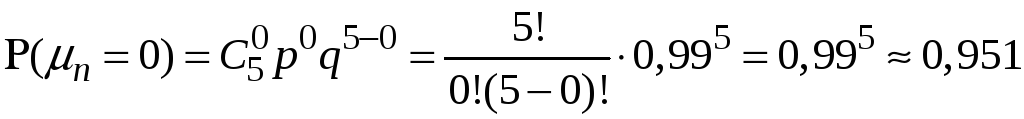б) В
даному випадку
.
За формулою (3):
.
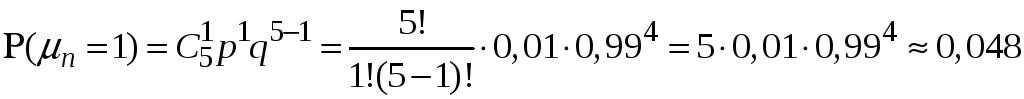в)
Помітимо, що наша подія «не менше 2
помилок» (
)
протилежна події «не більше 1 помилки»
(
),
яка дорівнює сумі двох попередніх подій.
Оскільки події
у схемі Бернуллі завжди несумісні (бо
не може одночасно з’явитися різна
кількість успіхів), то ймовірність події
«не більше 1 помилки» дорівнює сумі
ймовірностей подій «жодної помилки»
та
«рівно 1 помилка»
,
знайдених у пунктах а) та б). Тому
