5. Простіші властивості ймовірності

1) .

Дійсно, . Оскільки події і несумісні, то за аксіомами А2 і А3

,

звідки і випливає справедливість властивості 1.

2) .

Для доведення достатньо покласти в попередній формулі .

3) Для будь-яких подій і

.

Дійсно, (доведіть самостійно).

Події в правих частинах рівностей несумісні (доведіть самостійно), тому

,

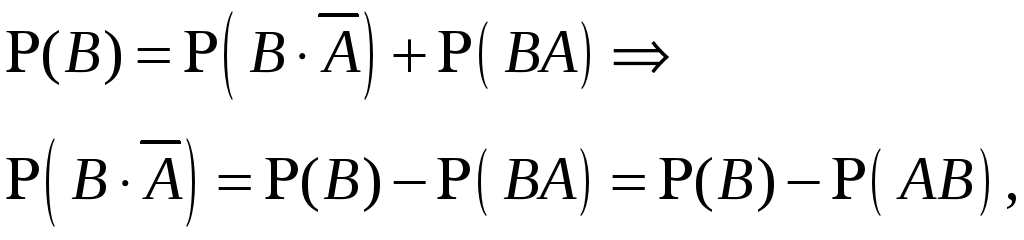
звідки і випливає вихідне твердження.

4) .

Випливає з властивості 3.

5) Якщо , то .

Доведіть самостійно.

6. Класичне означення ймовірності

Одним з можливих підходів до означення ймовірності є так зване класичне означення ймовірності.

Нехай - простір елементарних подій, алгебра подій складається з усіх підмножин простору . Вважають, що ймовірність кожної з елементарних подій дорівнює . Тоді ймовірність події обчислюється, як

.

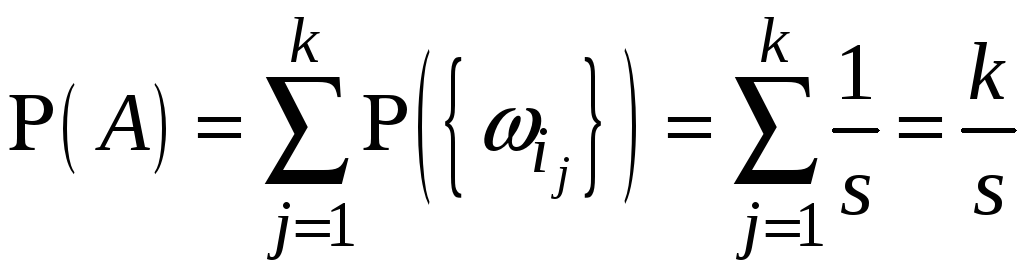Як бачимо, імовірність події дорівнює відношенню кількості елементарних подій , що входять у подію , до загальної кількості елементарних подій у просторі :

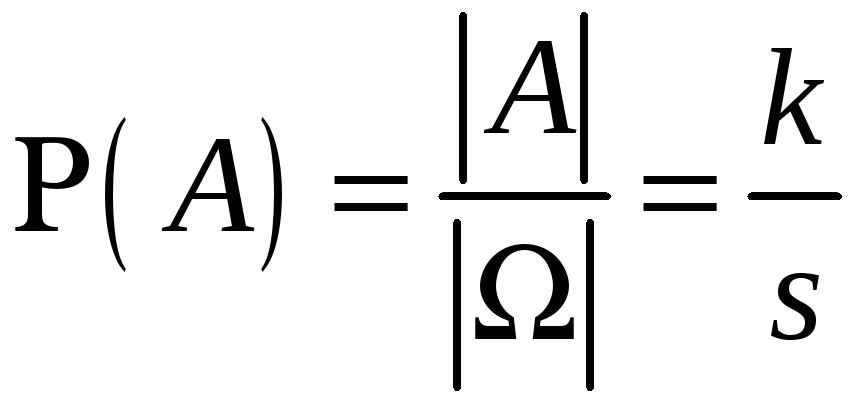, (1)

де через позначається кількість елементів множини .

Зауваження. Елементарні події, що входять у подію часто називають сприятливими подіями. Таким чином, з точки зору класичного означення, ймовірність випадкової події дорівнює відношенню кількості сприятливих елементарних подій до загальної кількості елементарних подій.

Задача. Довести, що визначена в цей спосіб функція задовольняє всі аксіоми ймовірності А1 – А4 і є, таким чином, імовірністю.

Класичне означення ймовірності є доброю математичною моделлю тих випадкових явищ, для яких результати досліду є симетричними, і тому природно вважати їх рівноможливими. Наприклад: задачі з області азартних ігор, лотерей і т.д., а також задачі організації вибіркового контролю і вибіркових статистичних досліджень.

Розглянемо дві найбільш поширені ймовірнісні схеми.

1. Схема випадкового вибору з поверненням.

Розглянемо набір з натуральних чисел . Через позначимо

довільний -вимірний вектор, всі координати якого належать вказаному

набору. Таким чином, в даній імовірнісній схемі розглядається простір елементарних подій

,

причому всі елементарні події рівноймовірні.

2. Схема випадкового вибору без повернення.

В даній імовірнісній схемі розглядаються елементарні події такі, що жодне значення координати не повторюється двічі:

,

причому всі елементарні події рівноймовірні.

Ці схеми можна інтерпретувати так: нехай в ящику міститься однакових кульок, помічених числами від до . З ящику по одній дістають кульок поспіль і їхні номери записують. Якщо кожну витягнену кульку відразу же повертають у ящик, то маємо схему 1, якщо кульки у ящик не повертаються – то схему 2. Іноді в другому випадку простіше вважати , що кульок дістають з ящика разом. При цьому об’єднуються елементарні події, що відрізняються тільки порядком номерів , тобто розглядається простір елементарних подій

.

Можна показати, що отримані схеми 2 и 2^/ еквівалентні.

У формулюваннях задач з теорії ймовірностей доволі часто вказується тільки описання експерименту або явища, а повне математичне формулювання не приводиться. Вважається, що розв’язання задачі мусить складатися з двох частин: 1) вибір моделі для описання даного умовами задачі явища і математичне формулювання задачі, 2) розв’язання математичної задачі.

Приклад.

З ящику, в якому міститься білих та чорних кульок, навмання витягують разом кульок. Знайти ймовірність того, що серед вибраних кульок буде рівно білих?

Розв’язання. Слово «навмання» в описаннях імовірнісних експериментів зустрічається доволі часто. В даній задачі вважається, що кульки були добре перемішані, що всі вони, за виключенням кольору, повністю однакові, що експериментатор кульок не бачить і на доторк розрізняти їх не може. В такому випадку розумним буде вважати, що все елементарні події у нашому експерименті рівноймовірні, і тому можна скористатися класичною схемою. Слово «разом» наводить нас на думку, що використовується схема випадкового вибору без повернення.

За елементарні події природно взяти будь-які підмножини з елементів, які беруться з множини у кульок. Відомо, що таких підмножин рівно

.

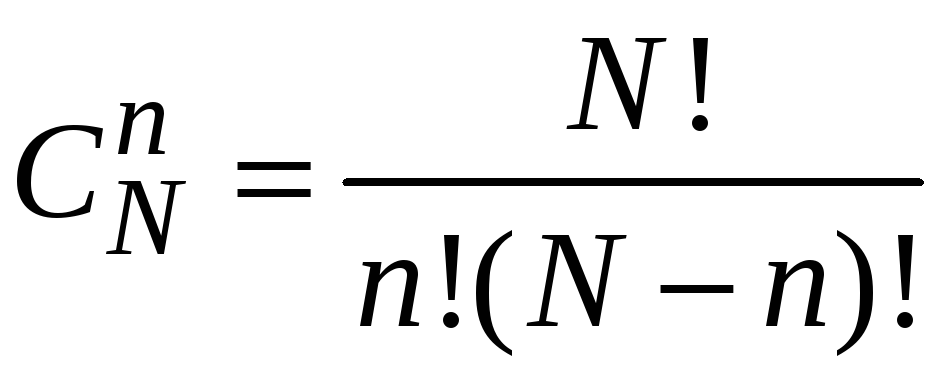Таким чином, у формулі класичної ймовірності (1) треба покласти .

Позначимо випадкову подію, яка досліджується у задачі, через . Цю подію можна розглядати, як множину наборів з кульок, причому кожен з наборів складається з двох частин: а) білих кульок і б) чорних кульок. Всі такі набори можна отримати наступним способом. Спочатку складаються усі можливі набори з білих кульок: усього білих кульок штук, тому вийде наборів. Потом складаються всі можливі набори з чорних кульок – таких наборів буде штук. Об’єднаємо кожен набір білих кульок с кожним набором чорних кульок, отримаємо довільний набір кульок, що належить множині .

Звідси випливає, що кількість сприятливих елементарних подій (елементарних подій, які входять у ) дорівнює . За формулою (1) ймовірність події дорівнює

, (2)

де . Набір чисел (2) називають гіпергеометричним розподілом.

Зрозуміло, що у даному прикладі кульки – це тільки корисний, найпростіший об’єкт імовірнісного експерименту. Отримана формула може бути застосованою для дослідження інших подібних процесів. Наприклад, в одній із задач вибіркового контролю замість кульок розглядаються виробів партії, що досліджується. Число бракованих виробів невідомо. Якщо всі вироби перевірити не можна, то з партії навмання відбирають невеличку кількість виробів . Якщо серед них з’являється бракованих, то вважають, що

.

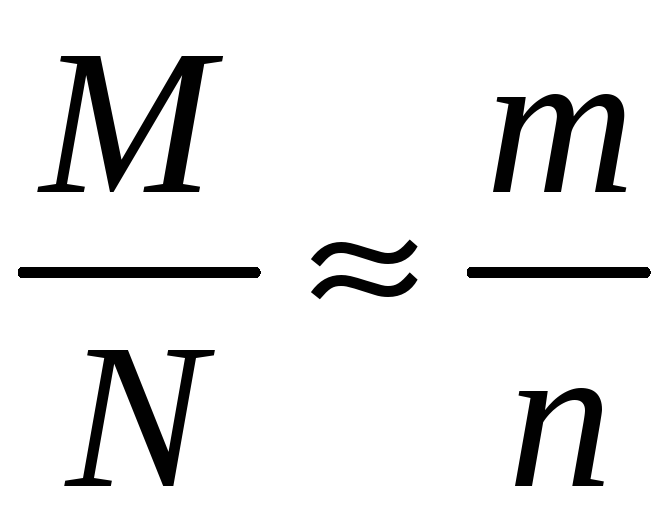Формула (2) застосовується для оцінки відхилення від . Величина у даному випадку – це ймовірність того, що у вказаній партії міститься рівно бракованих виробів.

Аналогічно можна оцінювати й невідомий параметр . Наприклад, у ставку виловлюють риб, мітять їх та відпускають у ставок. Через певний час повторно виловлюють риб. Якщо серед них з’являється помічених, то вважають, що

.

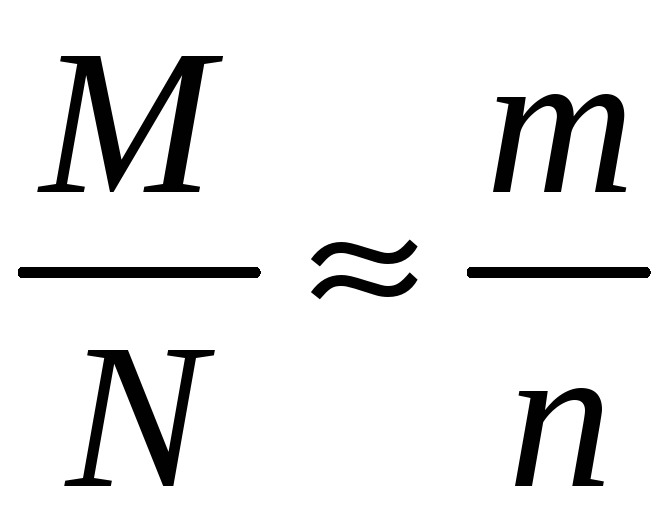Величина у даному випадку – це ймовірність того, що у ставку міститься риб.

За формулою (2) можна оцінювати ймовірність виграшу у лотерею. Припустимо, що Ви граєте у лотерею «6 з 49». Щоб отримати виграш, треба правильно помітити не менше 3 номерів. Позначимо цю подію . Через позначимо подію, яка полягає в тому, що Ви вгадали рівно номерів. Тоді протилежна подія – відсутність виграшу - дорівнює

.

За формулою (2) наближено обчислюємо

,

,

.

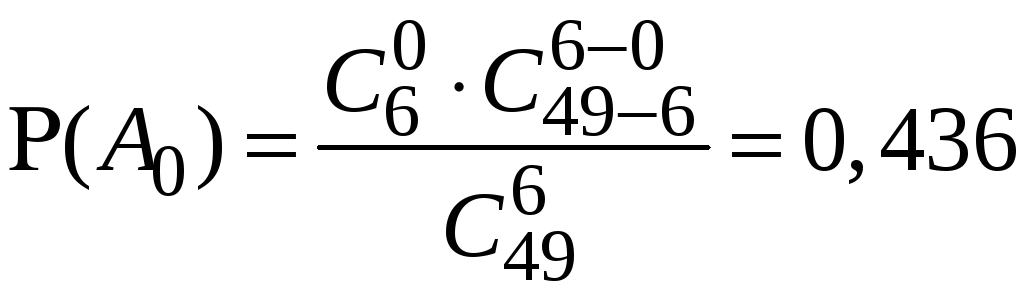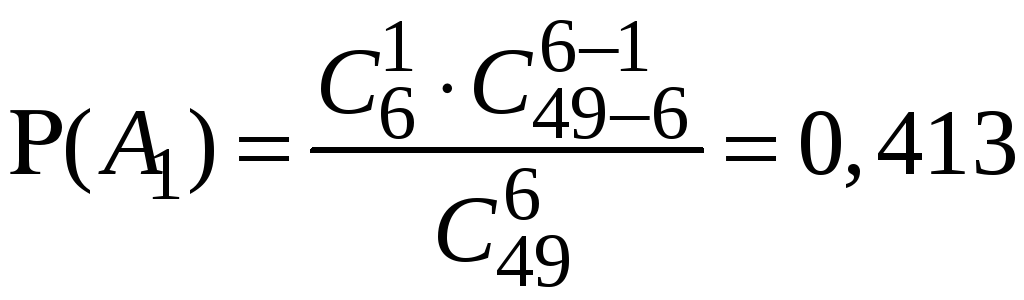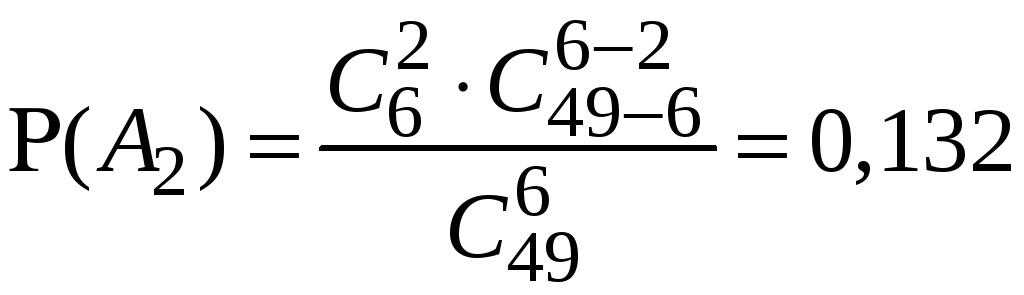За властивостями ймовірності

Звідси шукана ймовірність дорівнює.

,

тобто ймовірність отримати хоча б який-небудь виграш менше 2 відсотків.