9. Бескоалиционные игры. Определение бескоалиционной игры. Равновесные ситуации и стратегии.

Пусть имеется n игроков . Для каждого игрока i определено множество возможных способов действий данного игрока. Процесс игры заключается в выборе каждым игроком своей стратегии . Набор действий наз-ся ситуацией в игре. На каждом элементе определена система функций , кот. явл-ся функциями выигрыша для игроков соответственно.

Опр. Бескоалиционной игрой в нормальной форме называется совокупность

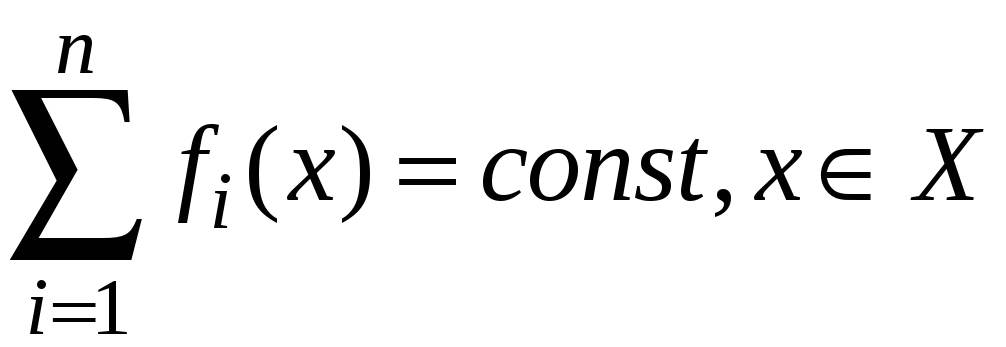На множестве бескоалиционных игр можно выделить игры с постоянной суммой выигрыша, т. е. , и с нулевой суммой выигрыша, т. е. .

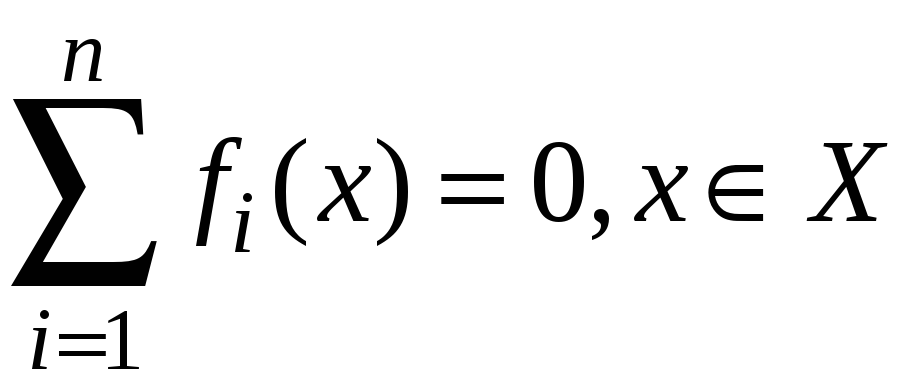Опр. Стратегия игрока наз-ся доминирующей по сравнению с , если выполнены неравенства. Аналогично определяется слабодоминируемая стратегия, для кот-ой.

Опр.Ситуация наз-ся приемлемой для игрока , если . Множество всех ситуаций, приемлемых для игрока i обозначим через .

Опр. Ситуация наз-ся ситуацией равновесия, если она является приемлемой ситуацией для всех игроков. Множество всех ситуаций равновесия обозначим через . Очевидно, .

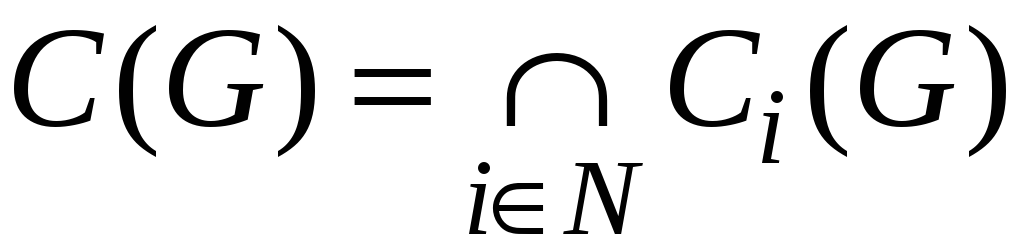Из определения видно, что в ситуации равновесия и только в ней ни один из игроков не заинтересован в отклонении от своих стратегий.

Вернёмся ко примеру1.

Для стороны а приемлемые ситуации — (в, а), (в, в), для стороны в — (а, в), (в, в).

(в, в) — ситуация равновесия.

10. Теорема Нэша для бескоалиционных игр.

Пусть игрок i имеет стратегий, произвольная смешанная стратегия игрока i, т. е. вектор компонентами которой являются вероятности выбора его чистых стратегий. Стратегии игроков будем отождествлять с точками евклидового пространства . Такой подход соответствует смешанному расширению бескоалиционной игры.

Теорема Нэша: Пусть в бескоалиционной игре количество игроков . Для каждого игрока мн-ва его стратегий компактно в . Ф-ции выигрышей непрерывны на множестве ситуаций , при любом наборе стратегий ф-ии выигрышей выпуклы вниз на , тогда в бескоалиционной биматричной игре ситуация равновесия.

Следствие: В конечной бескоалиционной игре существует ситуация равновесия, возможно в смешанных стратегиях.

Биматричная игра

Рассмотрим бескоалиционную игру двух игроков. Такая игра называется биматричной и обозначается . В качестве решения биматричной игры 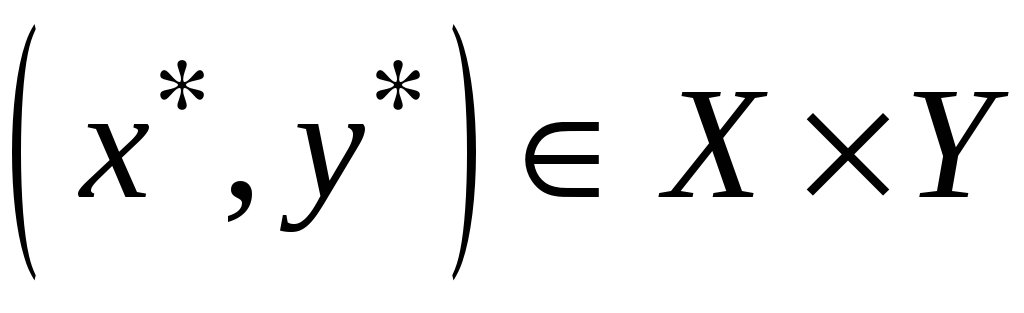рассматривается ситуация равновесия, для которой выполнены условия и .

Эти неравенства означают, что стратегия первого игрока является наилучшей реакцией на действия 2-го игрока, а стратегия явл. наилучшей реакцией 2-го игрока на действия 1-го.

Для любой стратегии находим стратегию , доставляющую наибольшее значение ф-ции выигрышей для 1-го игрока , т.е. .

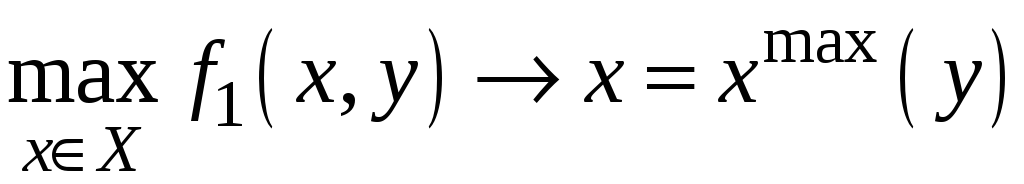Аналогичным образом, для найдем те , которые доставляют наибольшее значение для ф-ции выигрышей 2-го игрока , т.е. 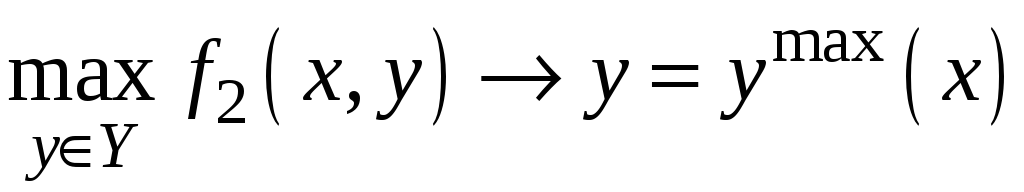. Объединяем полученные решения в систему уравнений:

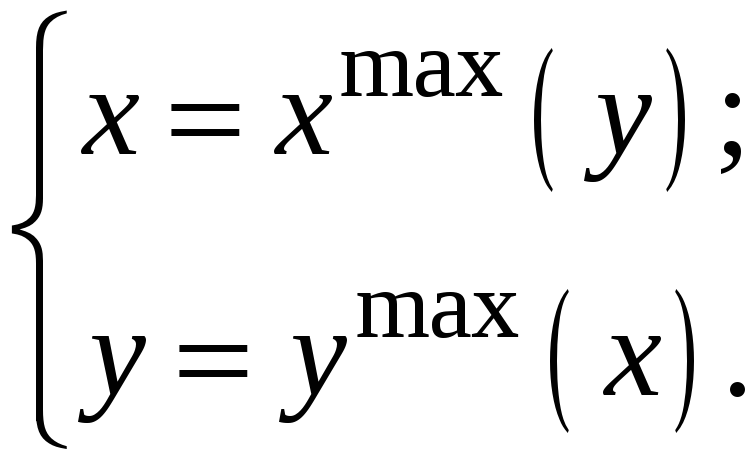
Данная система позволит нам найти ситуации равновесия.

11. Методы анализа сетей. Потоки на сетях.

Граф – пара двух мн-в , где - мн-во элементов произвольной природы, наз. Вершинами, - подмн-во всех пар элементов из . Неупорядоченная пара вершин наз. ребром, а упорядоченная – дугой. Граф, содержащий только ребра наз. неориентированным, а граф, содержащий только дуги – ориентированным.

Пример (неориентированного графа).

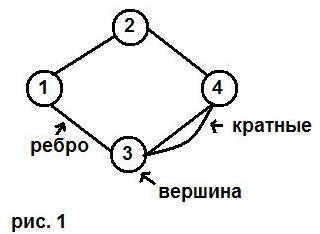
Пример (ориентированного графа).

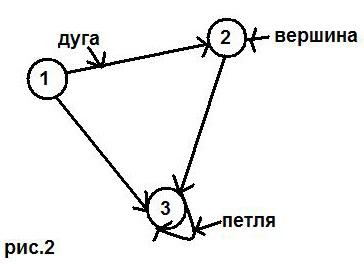
Если концевые вершины дуг (ребер) совпадают, то такие дуги (ребра) наз. петлей. Если пара вершин соединены двумя или более дугами (ребрами), то такие дуги (ребра), наз. кратными. Вершины, соединенные ребром или дугой, наз. смежными. Ребра, имеющие общую вершину, наз. смежными. Ребро (дуга) и любая из его двух вершин, наз. инцидентными.

Путем в графе наз. последовательность дуг , в которой конец каждой предыдущей дуги явл. начало следующей. Например, на рис. 2 путь , . Путь, у которого начальная вершина совпадает с конечной наз. контуром. Для неориентированного графа понятие, аналогичное пути, это цепь, а понятие, аналогичное контуру – цикл. На рис.1 цепь (1,2), (2,4), цикл – (1,2), (2,4), (4,3), (3,1).

Граф наз. конечным, если мн-ва и конечны. Граф наз. связным, если его любые две вершины можно соединить путем (цепью).

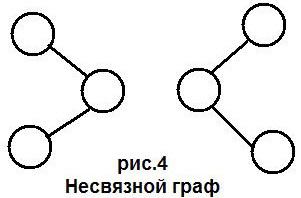
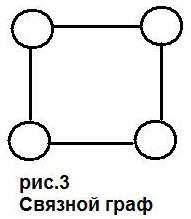
Если дугам графа приписаны числа (веса), то такой граф наз. взвешенным.

Сеть – взвешенный, конечный, ориентированный граф без петель с выделенной вершиной , называемой истоком, и выделенной вершиной , называемой стоком, причем дуги сети имеют направление от к .

Задача о максимальном потоке. Разрывы в сетях.

Сформулируем задачу о нахождении максимального потока на сети. Найти такую совокупность 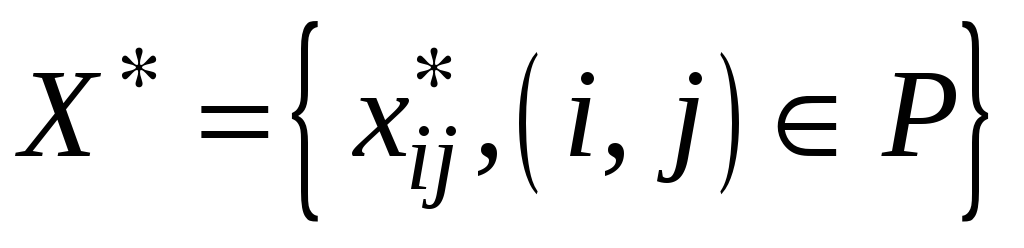потоков по дугам, которая удовлетворяет условиям

(1)

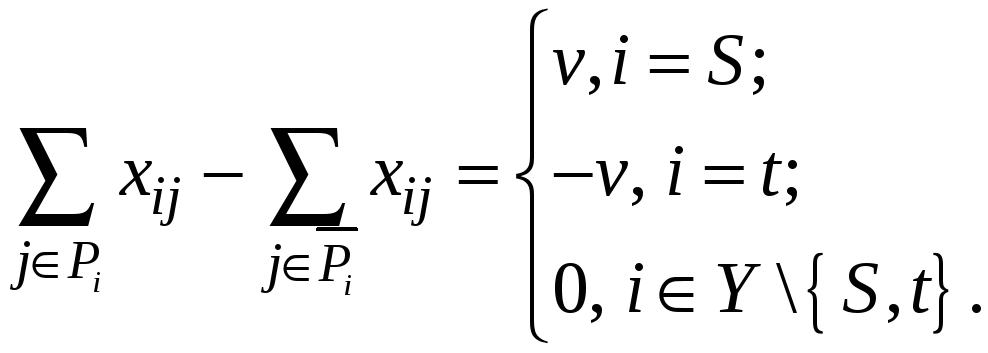(2)

и максимизирует линейную ф-цию (3).

Задача (1)-(3) наз. ЗЛП и может быть решена любым годящимся способом решения ЗЛП. Однако, специфика ограничений задач (2)-(4) предполагает поиск специального метода решения данной задачи.

Анализ сети легче проводить, если она правильно пронумерована. Сеть наз. правильно пронумерованной, если для любой дуги .

Алгоритм Фалкерсона правильной нумерации сети:

1. Рассматриваем все вершины, в которые не входит ни одна дуга и нумеруем их с единицы в произвольном порядке.

2. Мысленно удаляем все пронумерованные вершины вместе с инцидентным им дугам.

3. Вершины, которые стали начальными в результате удаления нумеруем начиная с последующего номера в произвольном порядке. Возвращаемся к шагу 2.

4. Шаги 2, 3 повторяем до тех пор, пока не будут пронумерованы след. вершины

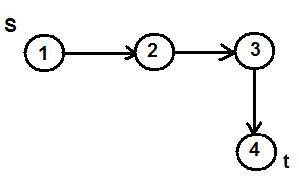
Рассмотрим такой случай

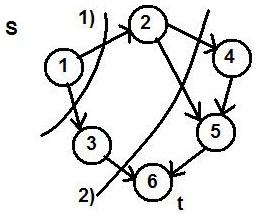
Разрезом сети , отделяющим исток от стока , наз. мн-во дуг , которые имеют начало в мн-ве , а конец в мн-ве , т.е. и - подмн-ва такие, что исток , а сток .

. Для того, чтобы задать разрез, достаточно задать мн-во .

Для последнего рассмотрим наши случаи:

1)

2)

Лемма 1: Пусть задана некоторая сеть . Тогда путь из вершины в вершину содержит по крайне мере одну дугу, принадлежащую одному разряду.

Док-во: Пусть задан разрез . Рассмотрим произвольный путь . Поскольку , , то обязательно наступит момент, когда , а . Тогда дуга принадлежит разрезу по определению.

Следствие: Если из сети удалить дуги произвольного разреза, то не останется пути из в .

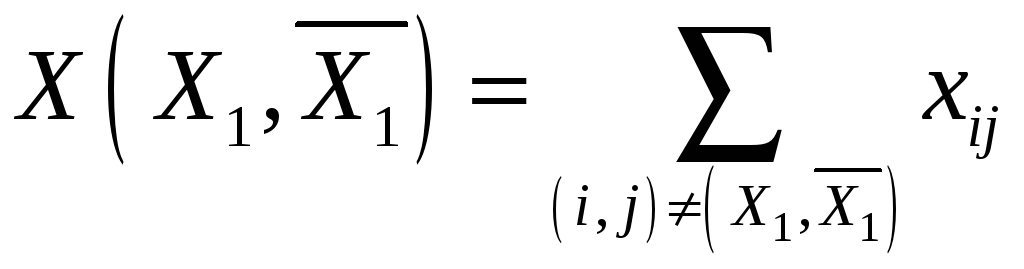Пусть на сети определен поток и задан некоторый разрез . Величина наз. потоком через разрез, а величина наз. пропускной способностью разреза.

Лемма 2(о величине потока на сети): Пусть задана сеть и некоторый поток на сети величины . Пусть некоторый разрез сети, тогда имеет место соотношение

(5)

Док-во: Запишем условие (5) в виде (6)

(7)

Просуммируем равенство (6) и (7) по всем вершинам мн-ва , получим: