6. Решение игры 22

Пусть имеем матричную игру 22 с платежной матрицей , которая не имеет седловой точки. В данном случае все стратегии игроков являются активными. Пусть первый игрок применяет смешанную стратегию тогда если игрок B применяет первую чистую стратегию, выигрыш . Аналогично, если игрок В применяет вторую чистую стратегию, выигрыш не изменится и будет равен .

Получаем систему для нахождения и :

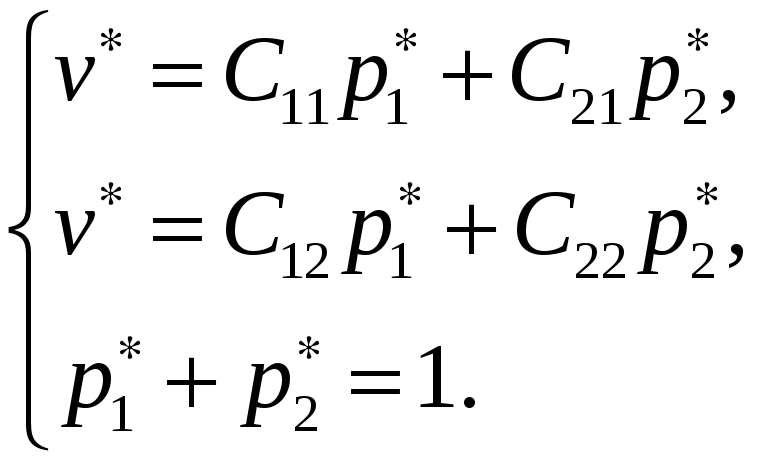
Решение этой системы следущее:

.

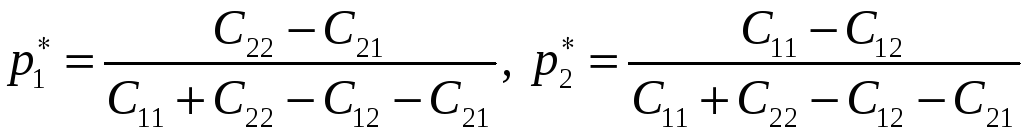
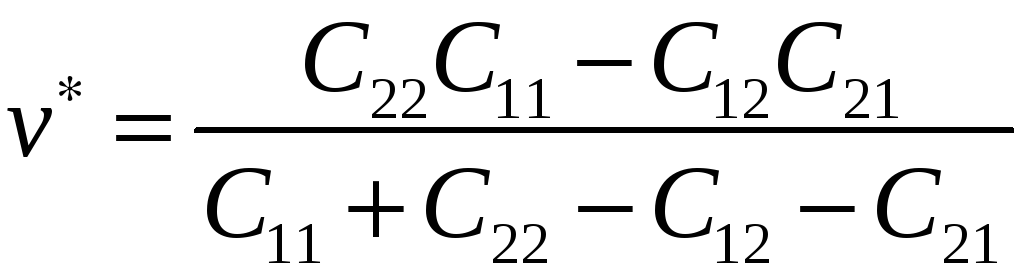Аналогично находим смешанную стратегию для игрока В из системы

Откуда

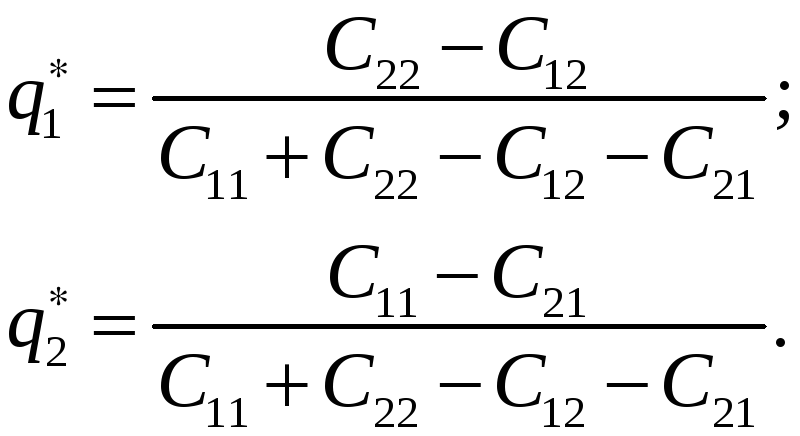
Графическое решение игр 2n b m2.

Рассмотрим матричную игру 2n с платежной матрице С. По оси Ох будем откладывать стратегии первого игрока. Координата х на оси абсцисс это вероятность (вероятность выбора стратегии ). Тогда расстояние от х до 1, т.е. - это вероятность (вероятность выбора стратегии ).

П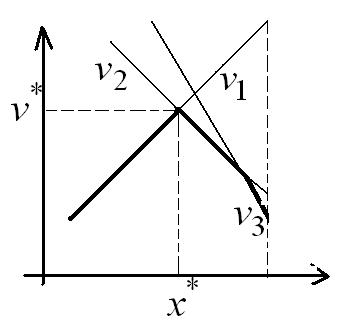усть второй игрок В выбрал свою j-ую чистую стратегию. Тогда средний выигрыш игрока А равен . По оси ординат будем откладывать средние выигрыши 1-го игрока в случае, когда он выбрал смешанную стратегию , а второй игрок чистую стратегию j.

В соответствии с принципом минимакса оптимальная стратегия 1-го игрока таковы, что min выигрыш его будет соответствовать нижней огибающей всех прямых соответствующих стратегиям 2-го игрока. Полученная огибающая обращена выпуклостью вверх, ее наивысшая точка определяет оптимальную стратегию 1-го игрока .

Определим оптимальную стратегию 2-го игрока. Возможны следующие случаи:

1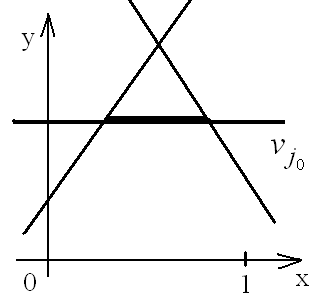). Огибающая имеет горизонтальный участок. Такое возможно в случае, когда , при этом оптимальной стратегией для второго игрока является чистая -ая стратегия.

2) Огибающая имеет пик

а) Пик имеет ноль или 1. Тогда оптимальная стратегия 1-го игрока чистая, а оптимальными стратегиями 2-го игрока являются те стратегии, которые соответствуют прямые подходящие к пиковой точке с положительным наклоном.

б) Пик лежит между 0 и 1. Пик имеет абсциссу не равную 0 или 1, если второй игрок откажется от всех остальных стратегий, кроме стратегий с номером и , то решение игры останется прежним. При этом мы можем воспользоваться результатами игры 22

, .

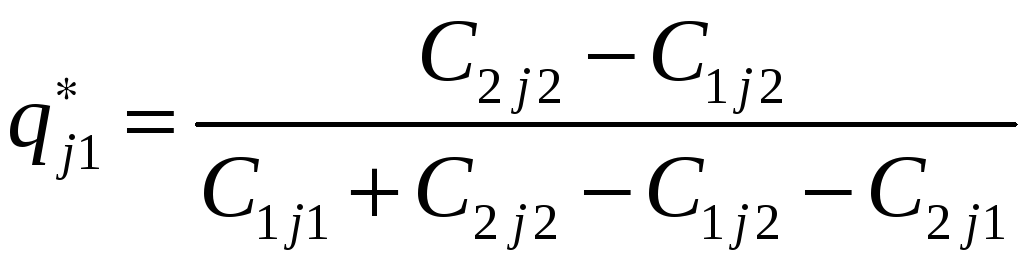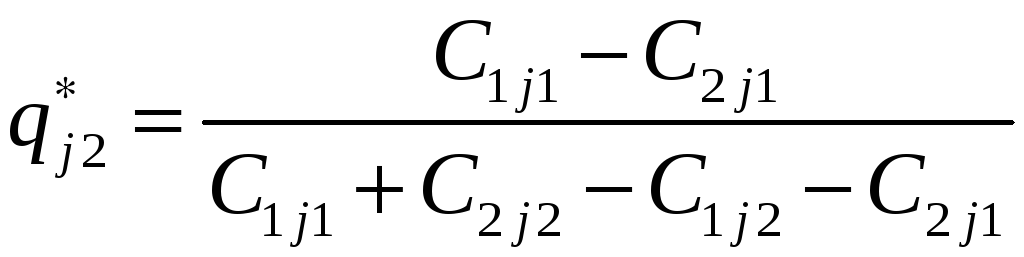Аналогично рассматривается графическое решение игры m2. Только при этом строится верхняя огибающая х ищется ее точка min.

7. Упрощение игр

Если игра mn не имеет седловой точки, то ее решение при больших mn может быть весьма затруднительным. Иногда удается упростить матрицу.

Опр1. Строка k доминирует строку l платежной матрицы С, если и .

В данном случае доминирующая строка не входит в оптимальную, поэтому строку l можно вычеркнуть из платежной матрицы.

Опр2. Столбец k доминирует столбец l платежной матрицы С, если и .

Доминируемые столбцы можно вычеркнуть из платежной матрицы.

Опр3. Строка k матрицы С дублирует строку l , если ,

Аналогично определяются дублирующие столбцы. Если в матрице есть дублирующие строки или столбцы, можно по одной из них вычеркнуть.

Иногда удается упростить матрицу путем замены чистых стратегий искусственными смешенными стратегиями.

П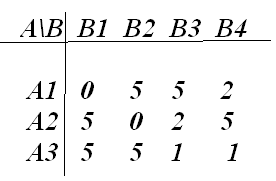ример.

В силу симметричности столбцов и соответствие чистых стратегий игрока В заключаем, что если они входят в оптимальную смешанную стратегию, то их вероятности равны.

Заменим указанные пары чистых стратегий смешанными для которых платежи равны среднему арифметическому платежей заменяемых стратегией.

Если искусственная смешенная стратегия вошла в оптимальную смешенную стратегию с вероятностью , то вероятности

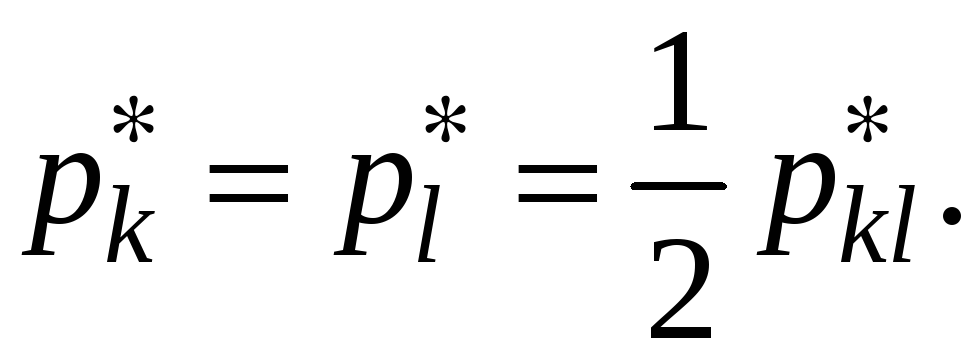
Алгоритм решения матричной игры m n.

Пусть задана матричная игра mn с платёжной матрицей С. Тогда игру можно решить следующим образом:

1) вычисляем верхнюю и нижнюю цену игры, т. е. находим и. Если =, то игра имеет решение в чистых стратегиях, следовательно, существует седловая точка — седловая точка, а решение игры есть тройка ,где .

2) если , то переходим к поиску решения смешанных стратегий, производим возможные упрощения матрицы.

3) если в платёжной матрице есть отрицательные элементы, то увеличиваем все её элементы до получения положительных, т. е. 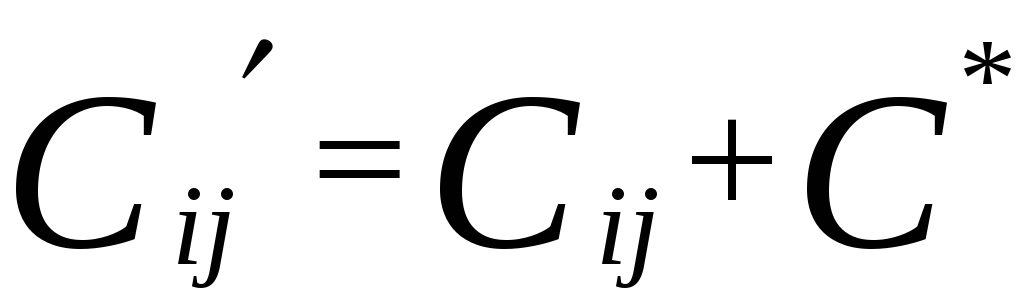при этом такая, что .

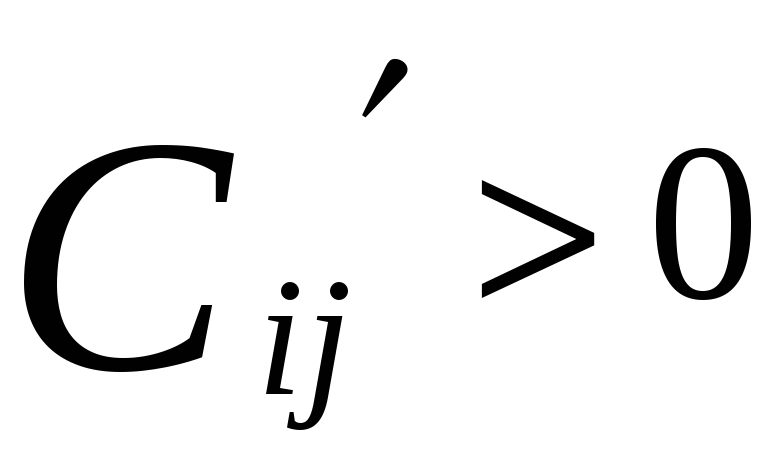4) для игры с платёжной матрицей сроим пару двойственных ЗЛП.

5) составленные задачи решаем любым способом, находи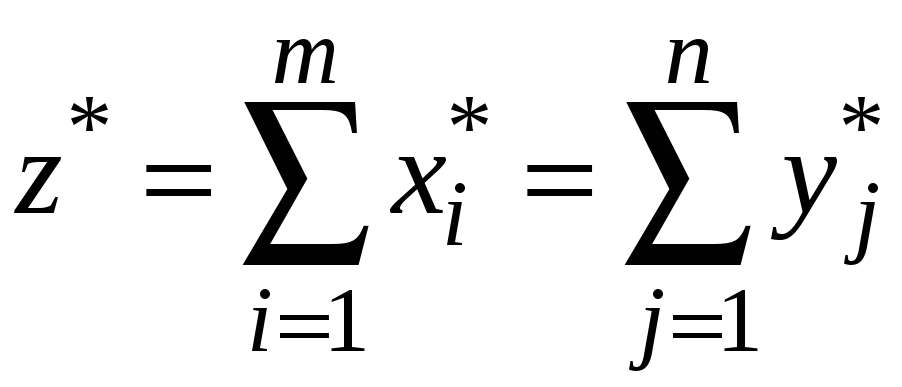м , , . Находим =.

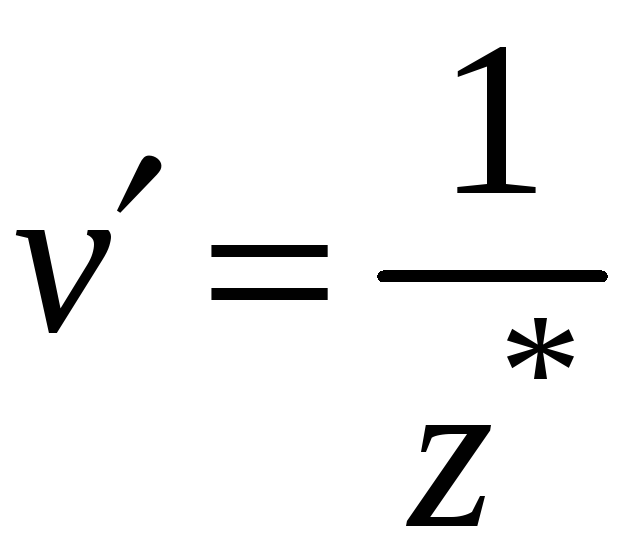6) решение исходной задачи получаем из соотношений , , ; , .

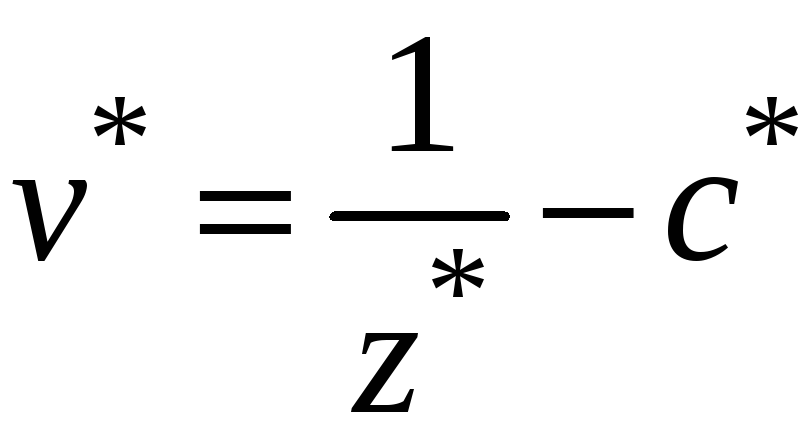7) если на втором шаге было выполнено упрощение платёжной матрицы, то вероятности доминируемых стратегий равно 0, вероятности дублируемых стратегий k и l находятся из соотношения

Если есть вероятность искусственно смешанной стратегии (k,l), то _.
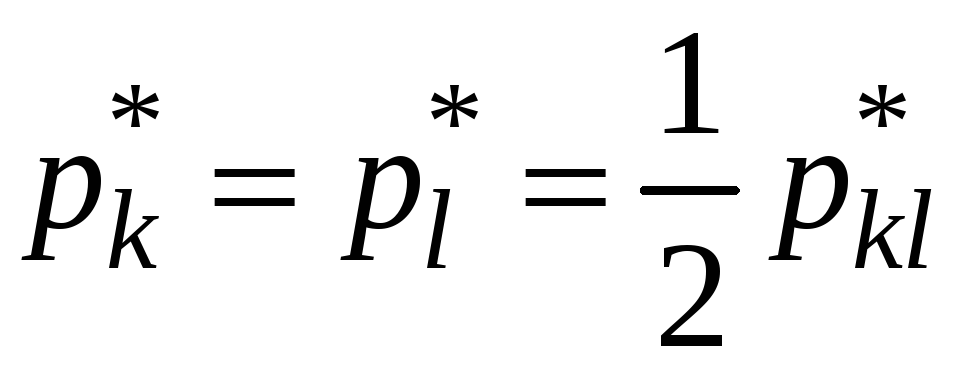