
- •1. Введение в исо. Предмет и история исо. Основные этапы и принципы операционного исследования. Постановка задач исо.
- •2. Постановка многокритериальной задачи.
- •3. Неопределенность природы и действий противника: принцип гарантированного результата
- •4. Основные понятия, принципы и классификация игр.
- •5. Решение матричных игр в смешанных стратегиях.
- •6. Решение игры 22
- •7. Упрощение игр
- •8. Игры с природой. Критерий Байеса
- •9. Бескоалиционные игры. Определение бескоалиционной игры. Равновесные ситуации и стратегии.
- •10. Теорема Нэша для бескоалиционных игр.
- •11. Методы анализа сетей. Потоки на сетях.
- •12. Теорема Форда-Фалкерсона
- •13. Комбинированные приложения з-чи о максимальном потоке. Простейшая з-ча о назначении.
- •I. Предварительный этап.
- •II. Этап расстановки пометок.
- •III. Этап переброски.
- •14. Классическая задача о назначении.
- •I этап. Приведение матрицы.
- •II этап. Выбор назначений.
- •III этап. Дополнительное приведение матрицы.
- •15. Основные этапы и понятия сетевого планирования и управления(спу)
- •17. Задача оптимального по времени распределения ограниченных ресурсов на сетевых графиках
- •19. Общая задача теории расписаний.
5. Решение матричных игр в смешанных стратегиях.
Пример (игра поиск): Имеются 2 игрока и 2 комнаты. Игрок А может спрятаться в одной из этих двух комнат, а игрок В ищет его в одной из двух комнат. Если игрок В находит игрока А, то игрок А выплачивает ему одну денежную единицу. В противном случае игрок В выплачивает игроку А одну денежную единицу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так
как
![]() ,
значит
,
значит
![]() .
Данная игра не имеет седловой точки и
не имеет решения в чистых стратегиях.
.
Данная игра не имеет седловой точки и
не имеет решения в чистых стратегиях.
Пусть
задана антагонистическая игра, в
платежной матрице которой нет седловой
точки. Решения в чистых стратегиях такая
игра не имеет. Согласно принципу минимакса
игрок А
может обеспечить себе выигрыш не меньше,
чем
![]() ,
а игрок В
проигрыш не больше, чем
,
а игрок В
проигрыш не больше, чем
![]() .
Рассм. возможно ли улучшение данного
результата если игроки откажутся от
своих максиминных и минимаксных
стратегий, а будут чередовать некоторые
стратегии случайным образом.
.
Рассм. возможно ли улучшение данного
результата если игроки откажутся от
своих максиминных и минимаксных
стратегий, а будут чередовать некоторые
стратегии случайным образом.
Опр. Случайный вектор, координаты которого определяют вероятности применения чистых стратегий того или иного игрока наз-ся смешанной стратегией.
Смешанную
стратегию для игрока A
обозначим
![]() (
(
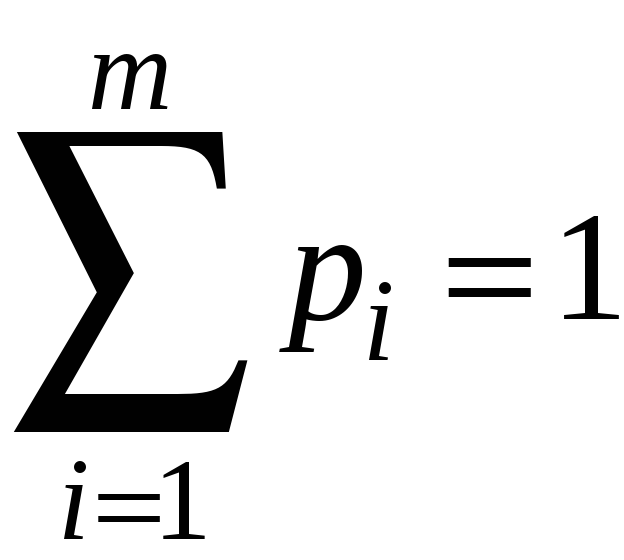 ).
Для игрока В
смешанную
стратегию обозначим
).
Для игрока В
смешанную
стратегию обозначим
![]() (
(
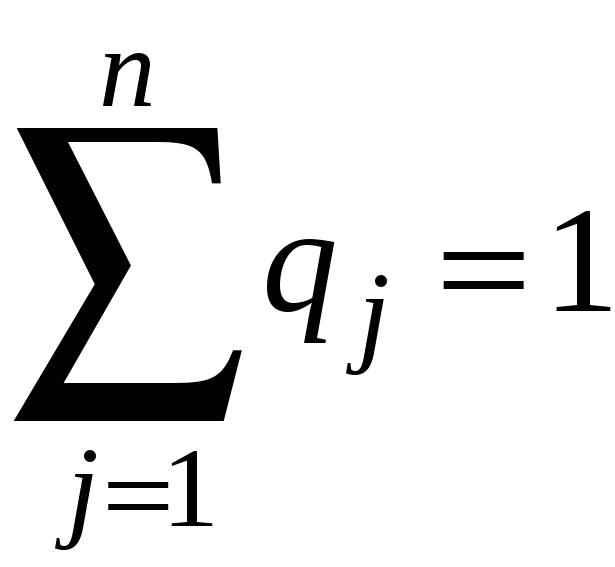 ).
).
Здесь
![]() – вероятности применения игроками A
и В
стратегий
– вероятности применения игроками A
и В
стратегий
![]() и
и
![]() соответственно. Обозначим через P
и Q
множества стратегий для игроков A
и В
соответственно.
соответственно. Обозначим через P
и Q
множества стратегий для игроков A
и В
соответственно.
Величина
выигрыша при использовании смешанных
стратегий p
и q
случайна и равна
![]() (С – платежная матрица игры).
(С – платежная матрица игры).
Основная теорема теории игр
Опр.
Смешанные стратегии
![]() и
и
![]() называются оптимальными, если они
образуют седловую точку для платежной
функции
называются оптимальными, если они
образуют седловую точку для платежной
функции
![]() ,
т.е.
,
т.е.
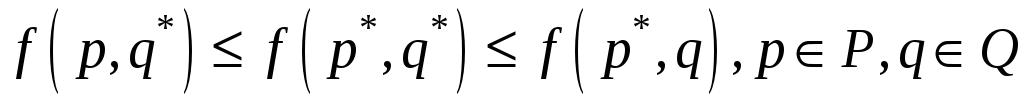 (1)
(1)
Выигрыш
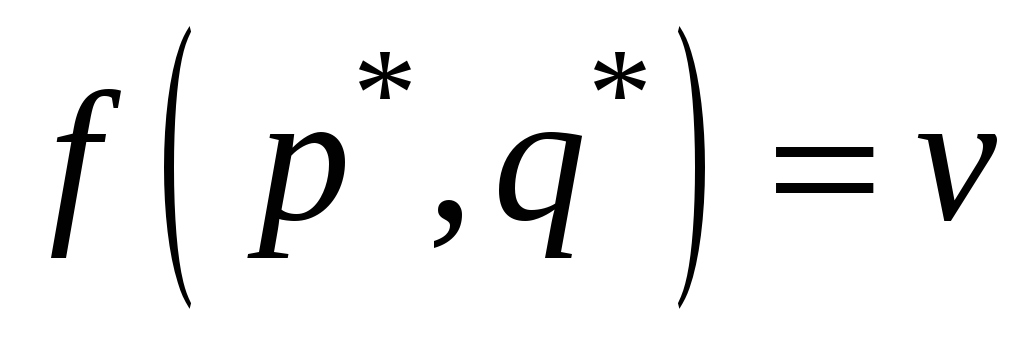 ,
соответствующий паре оптимальных
стратегий
,
соответствующий паре оптимальных
стратегий
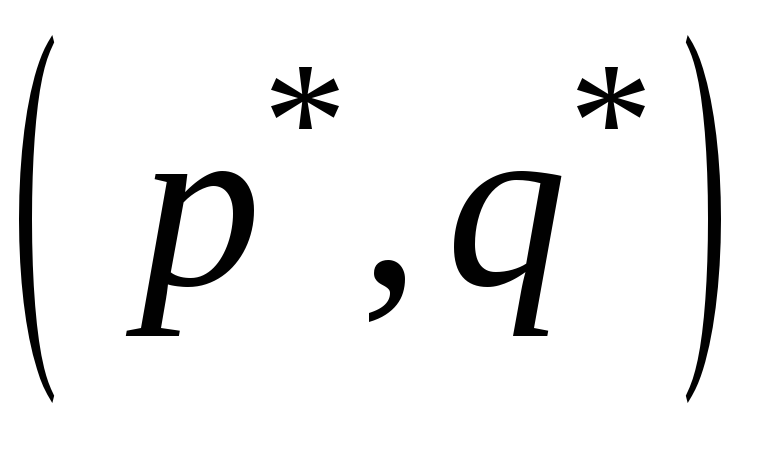 наз-ся ценой игры.
наз-ся ценой игры.
Теорема: Любая конечная матричная игра имеет решение в области смешанных стратегий.
Док-во.
Пусть
С- платежная матрица игры с положительными
элементами. Такое предположение не
ограничивает общности в дальнейших
рассуждениях, поскольку всегда можно
найти такое число, прибавив кот. мы
матрицу, содержащую только положительные
элементы, при этом множество оптимальных
стратегий для этих двух игр совпадает,
а цена игр увеличивается на данное
положительное число. Покажем, что
матричная игра сводится к паре двойственных
задач линейного программирования,
которые имеют решение. Пусть игрок А
использует
свою оптимально смешанную стратегию
![]() ,
а игрок В
некот. j-ую
чистую стратегию q.
Тогда полученный выигрыш будет
удовлетворять нер-ству
,
а игрок В
некот. j-ую
чистую стратегию q.
Тогда полученный выигрыш будет
удовлетворять нер-ству
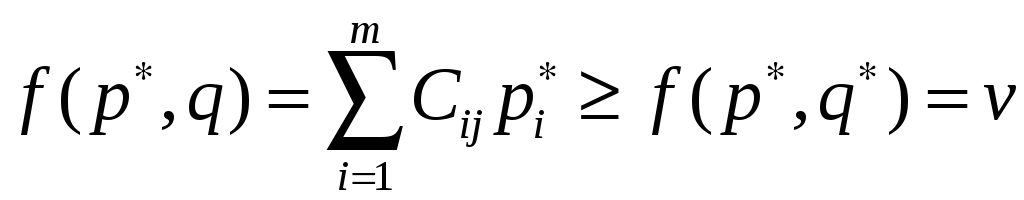 .
.
Введем
переменную
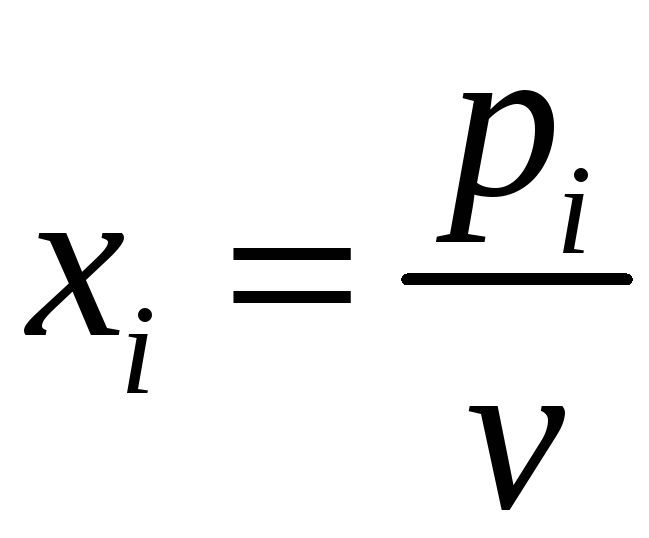 .
Рассмотрим
.
Рассмотрим
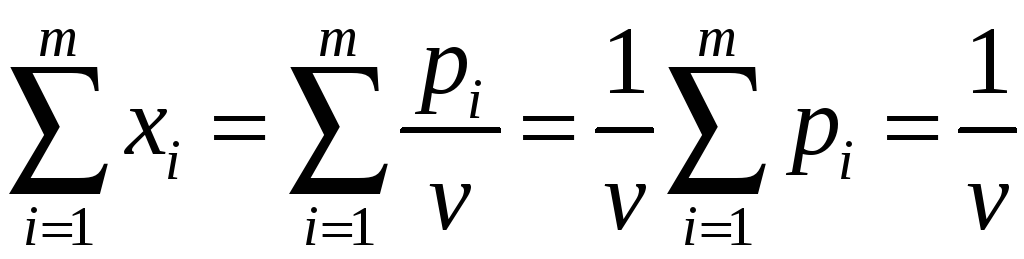 .
Поскольку первый игрок стремится
максимизировать свой выигрыш, то его
цель можно записать следующим образом
.
Поскольку первый игрок стремится
максимизировать свой выигрыш, то его
цель можно записать следующим образом
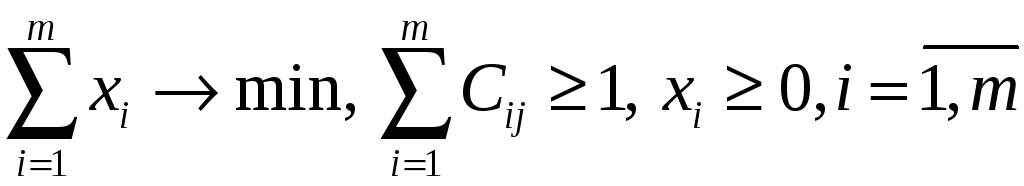 (2)
(2)
Обозначим
через
![]() - оптимальную смешанную стратегию игрока
В.
Пусть игрок А
использует
некоторую
i-ую
стратегию p.
При этом выигрыш удовлетв. след. нер-ву
- оптимальную смешанную стратегию игрока
В.
Пусть игрок А
использует
некоторую
i-ую
стратегию p.
При этом выигрыш удовлетв. след. нер-ву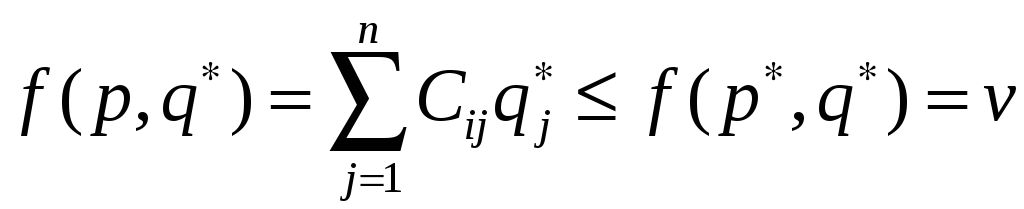 .
Вводя обозначения
.
Вводя обозначения
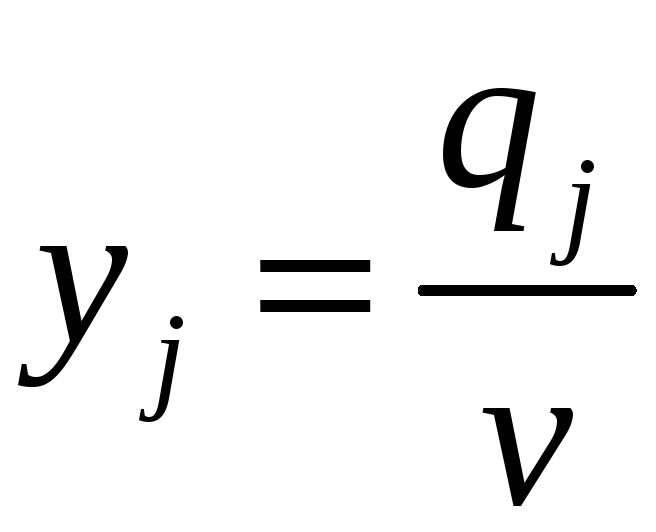 получим следующую задачу линейного
программирования, относительно интереса
игрока В.
получим следующую задачу линейного
программирования, относительно интереса
игрока В.
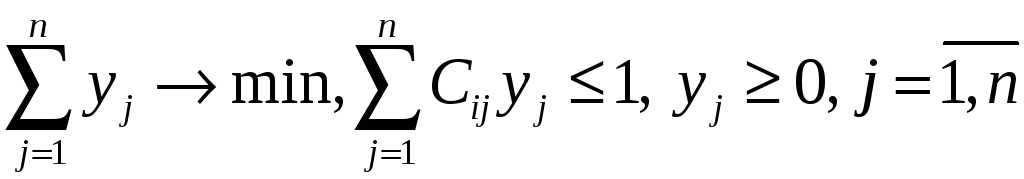 (3)
(3)
Заметим,
что (2) и (3) являются парой взаимнодвойственных
задач линейного программирования.
Согласно теоремы двойственности, задачи
(2) и (3) имеют решения одновременно.
Отметим, что целевая функция задачи (2)
ограничена снизу нулем и решение
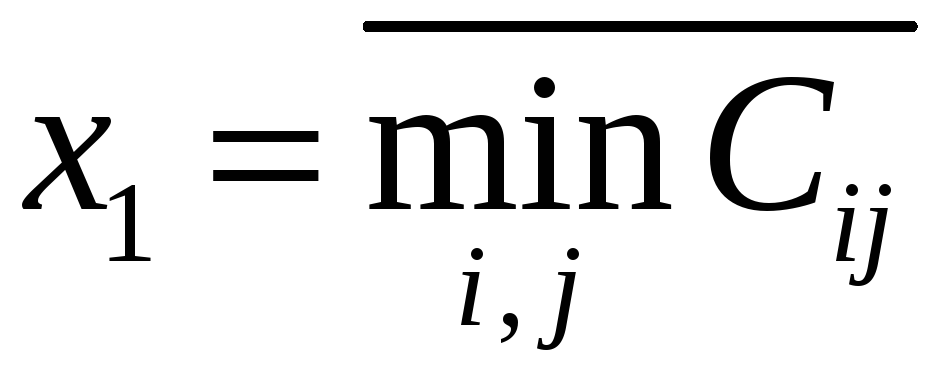 ,
,
![]() .
Это решение является планом задачи (2),
следовательно, задача (3) имеет решение.
Если
.
Это решение является планом задачи (2),
следовательно, задача (3) имеет решение.
Если
![]() -
решение задачи (2), то координаты вектора
-
решение задачи (2), то координаты вектора
![]() находятся следующим образом
находятся следующим образом
![]() .
Аналогично, если
.
Аналогично, если
![]() -
решение задачи (3), то
-
решение задачи (3), то
![]() ,
а
,
а
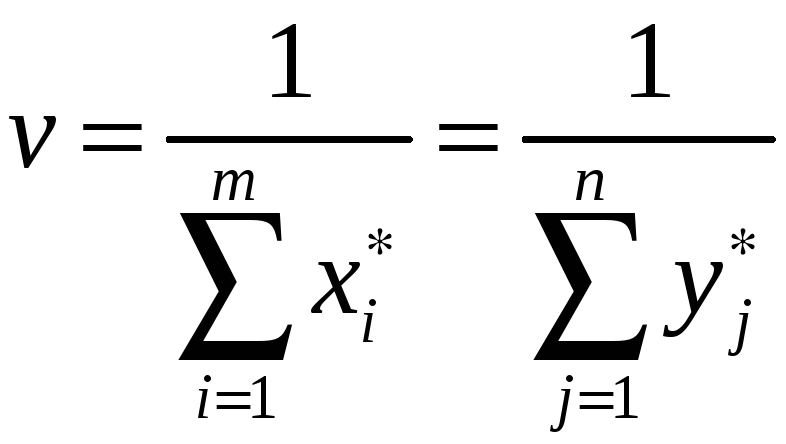 .
Значит, что если на первом шаге
производилось преобразование платежной
матрицы, то из полученной цены игры
следует вычесть положительную величину,
которая прибавлялась для получения
положительно матрицы.
.
Значит, что если на первом шаге
производилось преобразование платежной
матрицы, то из полученной цены игры
следует вычесть положительную величину,
которая прибавлялась для получения
положительно матрицы.
Активные стратегии. Теорема об активных стратегиях.
Опр. Будем говорить, что чистая стратегия i активна, если она входит в оптимальную смешанную стратегию с ненулевой вероятностью.
Теорема. Если один из игроков применяет свою оптимальную смешанную стратегию, то выигрыш останется неизменным и равным цене игры v независимо от того, что делает второй игрок, если тот не выходит за пределы своих активных стратегий, т.е. использует их в чистом виде или смешивает произвольным образом.
Док-во.
Пусть первые к
стратегий
для игрока А
–
активны, т.е.
![]() и соответственно первые
и соответственно первые
![]() стратегий
игрока В
также
активны, т.е.
стратегий
игрока В
также
активны, т.е.
![]() .
Пусть игрок А
применяет
свою стратегию
.
Пусть игрок А
применяет
свою стратегию
![]() ,
а игрок В-
некоторую чистую активную стратегию
j,
при этом полученный выигрыш обозначим
через
,
а игрок В-
некоторую чистую активную стратегию
j,
при этом полученный выигрыш обозначим
через
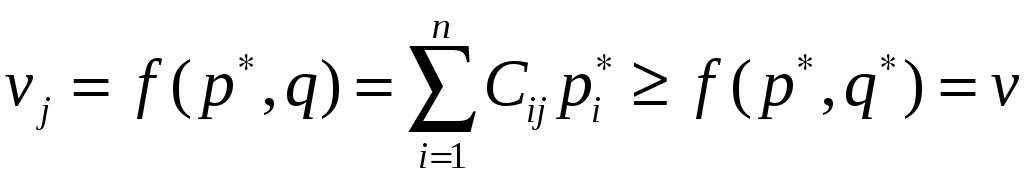 .
Выразим через
.
Выразим через
![]() цену игры
цену игры
![]() ,
т.е.
,
т.е.
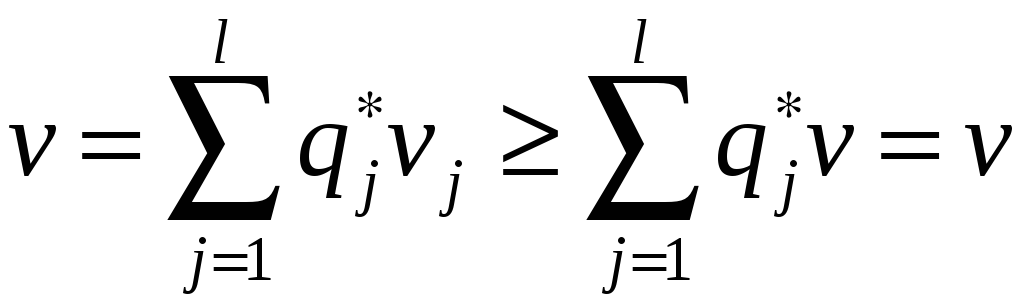 .
Если мы предположим, что
.
Если мы предположим, что
![]() ,
следовательно
,
следовательно
![]() противоречие.
противоречие.
