17. Задача оптимального по времени распределения ограниченных ресурсов на сетевых графиках

Пусть задан сетевой график (СГ), на дугах работах кот. на ряду с длительностью указана интенсивность потребления некоторого ресурса , а также общий имеющийся ресурс R. Пусть на протяжении выполнения всего проекта величины и R остаются постоянными.

Если работы выполняются в порядке временных параметров может возникнуть ситуация, что в некотором промежутке времени суммарное кол-во ресурсов превышает имеющийся ресурс R. В связи с этим возникает необходимость отнять некоторые из работ, что может привести к увеличению критич. времени. Задача состоит в том, чтобы определить календарный план проекта таким образом, что на любом промежутке времени суммарное кол-во потребл. ресурсов не превосходит R, а критич. время минимально. Рассм. эвристический алгоритм решения задачи.

Вся временная ось разбивается на интервалы . полагают равным самой левой точке из концов работ. Работы, расположенные над рассм. интервалами, нумеруем в порядке возрастания полных резервов, а при одинаковых резервах в порядке убывания интенсивности ресурсов. Далее производится накопление ресурса в порядке возрастания номеров. Работа, на кот. суммарное кол-во ресурсов становится больше, чем R, сдвигается. Также сдвигаются работы следующие за ней и все работы, связанные с ними.

Общий к-ый шаг. Пусть на интервале суммарное кол-во ресурсов не превышает R. Рассм. интервал . Точка получается как крайняя левая проекция начал и концов всех последующих работ.

Рассм. все работы над интервалами . Для всех работ, начинающихся после момента расчит. новые полные резервы с учетом сдвига. Если после сдвига критическое время не изменится, то полные резервы уменьшаются на величину сдвига.

Далее процедура нумерации и сдвиг работ, наход-ся над интервалом , осуществляется исходя из условия

1. Работы допуск. перерыв

2. Работы не допуск. перерыв.

В 1-м случае сдвигу подлежит не вся работа, а только часть после момента .

Во 2-м случае рассчит-ся разности между пересчит. полными резервами работ, начатых до момента и их продолжит. до момента . Работы нумеруем в порядке возрастания их разности, а в случае их совпадения в порядке убывания интенсивности ресурса.

19. Общая задача теории расписаний.

Пусть имеется приборов, на которые в момент времени поступает заявок. Каждая заявка характеризуется мн-вом индексов . Для каждой заявки определена последовательность , которая задает порядок обработки - ой заявки на приборах. Число 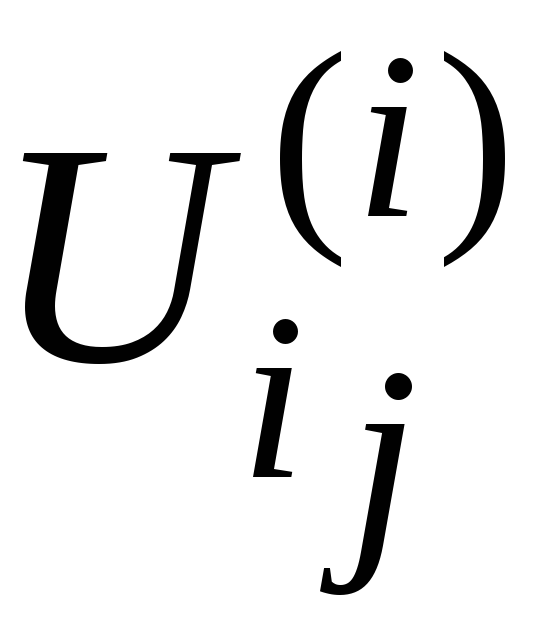- номер обслуживающего прибора. В соответствии с технолог. нормами задаются длительности обработки - ой заявки - ым прибором.

Рассмотрим процесс обработки заявок, удовлетв. след. св-ам:

Ни одна заявка не может быть обслужена одновременно неск-ми приборами;

Один прибор может обслуживать только одну заявку;

Если обслуживание - ой заявки - ым прибором началось в момент , то оно непрерывно продолжается до момента ;

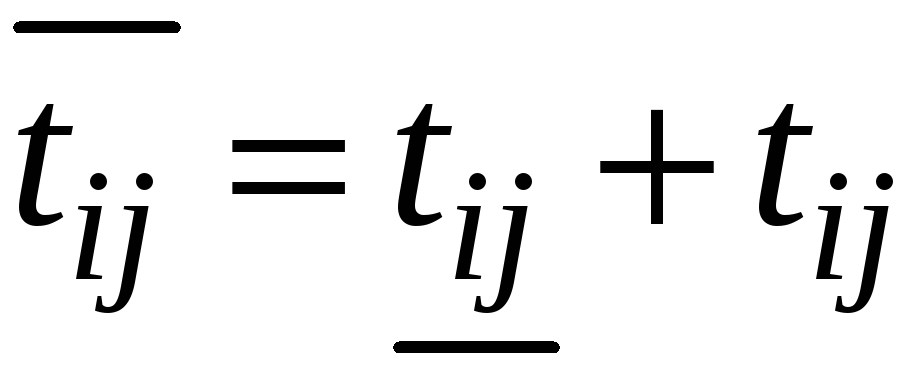Не учитывается время перехода заявок с одного прибора на другой;

Не учитывается время переналадки приборов.

Задача теории расписания

При заданных маршрутах и длительностях найти мом. Начала обслуживания каждой заявки на каждом приборе, так чтобы суммарное время обработки было минимальным.

Задача Белмана-Джонсона.

Наряду с предположениями

Ни одна заявка не может быть обслужена одновременно неск-ми приборами;

Один прибор может обслуживать только одну заявку;

Если обслуживание - ой заявки - ым прибором началось в момент , то оно непрерывно продолжается до момента ;

Не учитывается время перехода заявок с одного прибора на другой;

Не учитывается время переналадки приборов.

рассмотрим дополнительное условие, которое не ограничивает общности результата.

1. Технологические маршруты всех заявок одинаковы.

2. Порядок запуска заявок на устройства одинаков для всех приборов.

Очевидно, что любое расписание в этих предположениях можно представить в виде перестановки:

, где - номер очереди заявки .

Задача Джонсона. Пусть имеется два прибора, на котор. последовательно сначала на 1-ом, а затем на 2-ом должны пройти обработку заявок с заданными технологическими маршрутами.

Теорема(Джонсона). В оптимальном расписании заявка обслуживается раньше заявки , если .

На этой теореме основан алгоритм построения оптимального расписания для двух приборов.

Алгоритм Белмана-Джонсона – основан на идеи, сократить простой второго станка при полном исключении простоя первого.

Суть: резервируем пустую строку, состоящую из позиций. Исход. данные записываем в виде таблицы .

1 строка табл. – номер заявки.

2 строка – время обработки заявки на 1-ом приборе.

3 строка – время обработки заявки на 2-ом приборе.