
- •1. Введение в исо. Предмет и история исо. Основные этапы и принципы операционного исследования. Постановка задач исо.
- •2. Постановка многокритериальной задачи.
- •3. Неопределенность природы и действий противника: принцип гарантированного результата
- •4. Основные понятия, принципы и классификация игр.
- •5. Решение матричных игр в смешанных стратегиях.
- •6. Решение игры 22
- •7. Упрощение игр
- •8. Игры с природой. Критерий Байеса
- •9. Бескоалиционные игры. Определение бескоалиционной игры. Равновесные ситуации и стратегии.
- •10. Теорема Нэша для бескоалиционных игр.
- •11. Методы анализа сетей. Потоки на сетях.
- •12. Теорема Форда-Фалкерсона
- •13. Комбинированные приложения з-чи о максимальном потоке. Простейшая з-ча о назначении.
- •I. Предварительный этап.
- •II. Этап расстановки пометок.
- •III. Этап переброски.
- •14. Классическая задача о назначении.
- •I этап. Приведение матрицы.
- •II этап. Выбор назначений.
- •III этап. Дополнительное приведение матрицы.
- •15. Основные этапы и понятия сетевого планирования и управления(спу)
- •17. Задача оптимального по времени распределения ограниченных ресурсов на сетевых графиках
- •19. Общая задача теории расписаний.
13. Комбинированные приложения з-чи о максимальном потоке. Простейшая з-ча о назначении.
Пусть
имеется
![]() исполнителей и
исполнителей и
![]() работ. Каждый исполнитель может выполнить
лишь некоторые работы. Расставить
исполнителей на работы т.о., чтобы каждый
исполнитель выполнял не более одной
работы. Каждая работа выполнялась не
более одним исполнителем и общее
количество выполняемых работ было бы
максимальным.
работ. Каждый исполнитель может выполнить
лишь некоторые работы. Расставить
исполнителей на работы т.о., чтобы каждый
исполнитель выполнял не более одной
работы. Каждая работа выполнялась не
более одним исполнителем и общее
количество выполняемых работ было бы
максимальным.
Информация
о том, какие из работ способен выполнять
тот или иной исполнитель удобно
представить в виде матрицы
![]() ,
,
![]() ,
где элементы
,
где элементы
![]() ,
если
,
если
![]() -ый
исполнитель может выполнять
-ый
исполнитель может выполнять
![]() -ую
работу и
-ую
работу и
![]() - в противном случае.
- в противном случае.
Составим матем. модель данной задачи:
1)
введем управляемые переменные
![]() ,
которые могут принимать следующие
значения:
,
которые могут принимать следующие
значения:

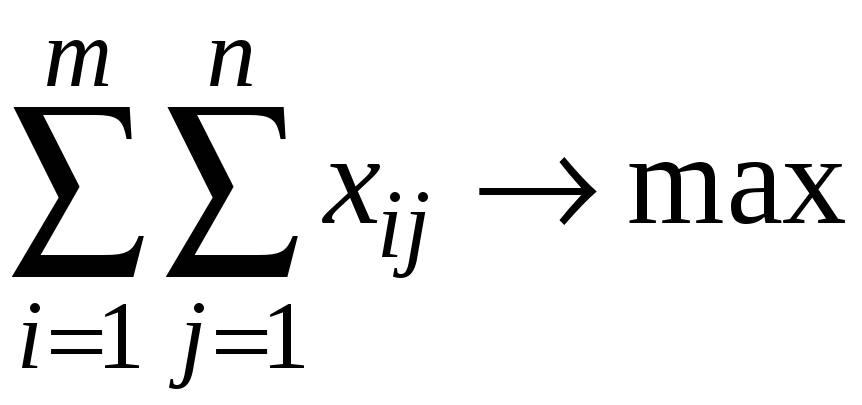 ;
;
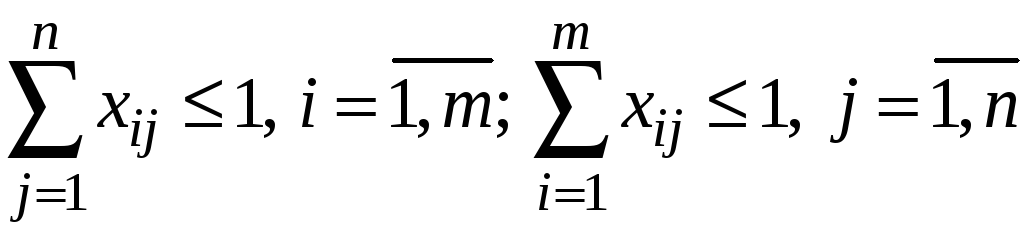 .
.
![]() .
.
Приведем графовую модель з-чи о назначении:
![]() ;
;
![]() -
мн-во всех исполнителей и работ;
-
мн-во всех исполнителей и работ;
![]() ;
;
![]() .
.
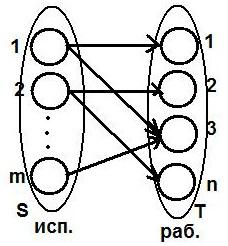
Опр.
Граф
![]() наз. двудольным,
если его мн-во вершин
наз. двудольным,
если его мн-во вершин
![]() можно разбить на два подмн-ва
можно разбить на два подмн-ва
![]() и
и
![]() т.о., что
т.о., что
![]() и любая дуга
и любая дуга
![]() соединяет вершину
соединяет вершину
![]() с вершиной
с вершиной
![]() .
.
Опр.
![]() - рассекающим
мн-вом наз. любое подмн-во вершин
двудольного графа, если при удалении
всех вершин этого мн-ва вместе с
инцидентными им дугами разрываются все
пути из
- рассекающим
мн-вом наз. любое подмн-во вершин
двудольного графа, если при удалении
всех вершин этого мн-ва вместе с
инцидентными им дугами разрываются все
пути из
![]() в
в
![]() .
.
Теорема Кенига-Эгервари.
Опр.
Граф
![]() наз. двудольным, если его множество
вернин Y
можно разбить на 2 подмножества S
и T
т.о., что
наз. двудольным, если его множество
вернин Y
можно разбить на 2 подмножества S
и T
т.о., что
![]() .
Любая дуга
.
Любая дуга
![]() соединяет вершину
соединяет вершину
![]() с вершиной
с вершиной
![]() .
.
Опр.
![]() -
рассекающим мн-вом называется любое
подмножество вершин двудольного графа,
если при удалении всех вершин этого
мн-ва вместе с инцидентными им дугами
разрываются все пути из
-
рассекающим мн-вом называется любое
подмножество вершин двудольного графа,
если при удалении всех вершин этого
мн-ва вместе с инцидентными им дугами
разрываются все пути из
![]() в
в
![]() .
.
Теорема.
Максимальное число дуг двудольного
графа
![]() попарно не имеющих общих вершин равно
минимальному кол-ву вершин в
попарно не имеющих общих вершин равно
минимальному кол-ву вершин в
![]() рассекающем мн-ве.
рассекающем мн-ве.
Д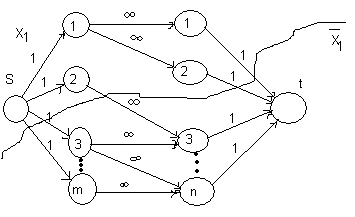 ок-во.
Сведем
двудольный граф
ок-во.
Сведем
двудольный граф
![]() к сети с одним истоком
к сети с одним истоком
![]() ,
и стоком
,
и стоком
![]() ,
также введем финивные дуги
,
также введем финивные дуги
![]() ,
,
![]() ,
пропускные способности которых положим
равными 1.
,
пропускные способности которых положим
равными 1.
Пропускные
способности двудольного графа положим
равными
![]() .
Решим на модифицированной сети задачу
о максимальном потоке. Пусть
.
Решим на модифицированной сети задачу
о максимальном потоке. Пусть
![]() - ф-ция, реализующая максим. поток на
сети.
- ф-ция, реализующая максим. поток на
сети.
![]() разрез сети. Рассмотрим мн-во дуг
разрез сети. Рассмотрим мн-во дуг
![]() .
Покажем, что мн-во
.
Покажем, что мн-во
![]() содержит дуги, попарно не имеющие общих
вершин. В каждую вершину мн-ва
содержит дуги, попарно не имеющие общих
вершин. В каждую вершину мн-ва
![]() может попасть поток, не превышающий 1.
По построению мн-ва
может попасть поток, не превышающий 1.
По построению мн-ва
![]() по каждой дуге этого мн-ва течет единичный
поток, следовательно, дуги мн-ва
по каждой дуге этого мн-ва течет единичный
поток, следовательно, дуги мн-ва
![]() не имеют общих начальных вершин.
Аналогично можно доказать, что дуги
мн-ва
не имеют общих начальных вершин.
Аналогично можно доказать, что дуги
мн-ва
![]() не имеют общих конечных вершин. Т.о. по
всем дугам мн-ва
не имеют общих конечных вершин. Т.о. по
всем дугам мн-ва
![]() бежит единичный поток, а по построению
данный поток максимален, сл-но, мощность
мн-ва
бежит единичный поток, а по построению
данный поток максимален, сл-но, мощность
мн-ва
![]() равно величине максимального потока:
равно величине максимального потока:
![]() .
.
Рассмотрим
мн-во
![]() .
Покажем, что
.
Покажем, что
![]() является
является
![]() -
рассекающим мн-вом. Положим обратное,
что
-
рассекающим мн-вом. Положим обратное,
что
![]() не явл-ся
не явл-ся
![]() -
рассекающим мн-вом, т.е. после удаления
всех вершин мн-ва
-
рассекающим мн-вом, т.е. после удаления
всех вершин мн-ва
![]() остается дуга
остается дуга
![]() такая, что
такая, что
![]() ,
т.е. сущ-ет ненасыщенная дуга
,
т.е. сущ-ет ненасыщенная дуга
![]() ,
помеченная вершина
,
помеченная вершина
![]() ,
не помеченная вершина
,
не помеченная вершина
![]() ,
которая может быть помечена, т.е.
,
которая может быть помечена, т.е.
![]() возникающее
противоречие док-ет, что мн-во
возникающее
противоречие док-ет, что мн-во
![]() явл-ся
явл-ся
![]() -рассекающим
мн-вом. Покажем, что мн-во
-рассекающим
мн-вом. Покажем, что мн-во
![]() -минимально.
Вершины этого мн-ва взаимно-однозначно
связаны с вершинами определяющим
минимальный разрез, т.е. либо явл-ся
началами, либо концами дуг разреза.
Поскольку построенный разрез минимален,
мощность мн-ва
-минимально.
Вершины этого мн-ва взаимно-однозначно
связаны с вершинами определяющим
минимальный разрез, т.е. либо явл-ся
началами, либо концами дуг разреза.
Поскольку построенный разрез минимален,
мощность мн-ва
![]() совпадает
со всей величиной потока:
совпадает
со всей величиной потока:
![]()
![]()
Приведем табличный аналог доказанной теоремы.
По
двудольному графу строим таблицу
![]() ,
где строки соот-ют исполнителям, а
столбцы ребятам;
,
где строки соот-ют исполнителям, а
столбцы ребятам;
![]() -
клетка считается допустимой, если
-
клетка считается допустимой, если
![]() ,
недопустимые клетки вычеркиваются.
,
недопустимые клетки вычеркиваются.
Опр. Две допустимые клетки наз. независимыми, если они не покрываются одним рядом.
Теорема. Максим. кол-во независимых допустимых клеток равно минимальному кол-ву рядов, покрывающих все допустимые клетки.
Алгоритм построения максим. мн-ва независимых допустимых клеток(ММНДК).
