
Зад лин прогр и мет их решения 16 12 08
.pdf
|
Никитенков В.Л., Холопов А.А. |
|
|
|
и |
|
методы их решения |
|
N |
|
LINEAR PROGRAMMING |
|
Сыктывкар 2008 |

Сыктывкарский государственный университет
Никитенков В.Л. Холопов А.А.
ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
И
МЕТОДЫ ИХ РЕШЕНИЯ
Учебное пособие и практикум
версия 16.12.08
Рекомендовано УМО по классическому университетскому образованию в качестве учебного пособия по методам решения задач математического программирования для студентов высших учебных заведений, обучающихся по специальности 010200 «Прикладная математика и информатика» и по направлению подготовки 511800 «Математика. Компьютерные науки»
Сыктывкар 2008

УДК 519.85 (075) ББК 22.1 Н 62
Никитенков В.Л., Холопов А.А.
Н 62 Задачи линейного программирования и методы их решения. Сыктывкар: Изд-во СыктГУ, 2008. 277 с. ISBN 978-5-87237-648-4
Вданном учебном пособии рассмотрены методы построения и решения задач математического программирования (построение математической модели, графический способ решения, прямой симплекс-метод, метод потенциалов для решения транспортной задачи, задачи об аренде оборудования, построение сетевых графиков и их анализ). Основные теоретические положения, методы и дополнительные задачи исследования операций приведены в специальном добавлении (двойственность, модифицированный симплекс-алгоритм, задачи раскроя, сетевая транспортная модель и родственные ей задачи). Материал сопровождается подробно разбираемыми примерами.
Впособии содержатся упражнения для самостоятельного решения и контрольные задания. Предназначено для студентов нематематических (а в добавлениях и математических) специальностей и лиц, занимающихся в системе заочного (дистанционного) образования и самообразованием.
Рецензенты:
Громов Н.А. – д.ф.-м.н., профессор, зав. отделом математики (Коми Научный Центр УрО РАН);
Полещиков С.М. – д.ф.-м.н., профессор, зав.кафедрой высшей математики (Сыктывкарский лесной институт С-Петербургской лесотехнической академии).
|
© Никитенков В.Л., Холопов А.А., |
2008 |
|
ISBN 978-5-87237-648-4 |
© ГОУ ВПО «Сыктывкарский государственный университет», |
2008 |
|
3
СОДЕРЖАНИЕ
Стр.
ВВЕДЕНИЕ……………………………………………………………………………..5 1.ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ДЛЯ ЭКОНОМИЧЕСКИХ ЗАДАЧ…………………………………………………………………………………5
1.1Задача планирования производства продукции (ЗЛП на максимизацию)…….5
1.2Задача о составлении оптимального рациона (ЗЛП на минимизацию)……….7
2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗЛП. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ЗЛП ОТ ДВУХ ПЕРЕМЕННЫХ С ОГРАНИЧЕНИЯМИ-
НЕРАВЕНСТВАМИ…………………………………………………………………7
3.СИМПЛЕКС-МЕТОД ДЛЯ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ………………………………………………………….15
3.1Предварительные сведения……………………………………………………..15
3.2Геометрическая идея симплекс-метода………………………………………..18
3.3Алгоритм прямого симплекс-метода…………………………………………...20
3.4Метод искусственных переменных. Вспомогательная задача ЛП…………...31
4.ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ……….38
4.1Постановка транспортной задачи………………………………………………38
4.2Метод потенциалов для решения ТЗ…………………………………………...41
4.3Пример решения классической транспортной задачи...……………………...56
5.ЗАДАЧА ОБ АРЕНДЕ ОБОРУДОВАНИЯ…………………...…………………..66
5.1Предварительные сведения. Бесконтурные сети…...........................................66
5.2 |
Планы аренды. Постановка задачи...................................................................... |
67 |
5.3 |
Сетевая модель задачи и её решение .................................................................. |
69 |
5.4 |
Табличный метод решения задачи...................................................................... |
70 |
6. СЕТЕВОЕ ПЛАНИРОВАНИЕ................................................................................. |
72 |
|
6.1 |
Предмет сетевого планирования ......................................................................... |
72 |
6.2 |
Структурное планирование.................................................................................. |
72 |
6.3 |
Календарное планирование.................................................................................. |
83 |
7. ДОБАВЛЕНИЯ.......................................................................................................... |
94 |
|
7.1Векторы и матрицы……………………………………………………………...94
7.2Постановка задачи ЛП…………………………………………………………..97
7.3Выпуклость множества допустимых решений ЗЛП…………………………..98
7.4Характеристика угловых точек…………………………………………………99
7.5Достижимость оптимального решения ЗЛП в угловой точке множества допустимых решений………………………………………………………….. 100
7.6 Условия разрешимости ЗЛП. Конечность способа перебора вершин........... |
102 |
|
7.7 Критерий оптимальности................................................................................... |
102 |
|
7.8 Улучшение текущего базисного решения ЗЛП. Критерий неограниченности |
||
целевой функции на множестве решений ....................................................... |
104 |
|
7.9 Базисная матрица нового решения ЗЛП. Левый мультипликатор. Формулы |
||
исключения Гаусса-Жордана............................................................................ |
107 |
|
7.10 |
Пары двойственных задач. Теоремы двойственности .................................. |
111 |
7.11 |
Матричная транспортная задача (ТЗ) ............................................................. |
124 |
7.12 |
Модифицированный алгоритм симплекс-метода.......................................... |
127 |
7.13 |
Задачи раскроя .................................................................................................. |
143 |
7.13.1 Постановка задачи..................................................................................... |
143 |
|
7.13.2 Генерирование способа раскроя. Метод ветвей и границ..................... |
144 |
|
7.13.3 Генерирование способа раскроя. Рекуррентные соотношения |
|
|
|
Беллмана (метод динамического программирования)........................ |
148 |
7.13.4. Особенности форматного раскроя бумажного полотна....................... |
155 |
|
7.14 Сетевая транспортная задача и связанные с ней экстремальные задачи на |
|
|
4 |
|
графах (сетях).................................................................................................... |
193 |
7.14.1 Основные сведения из теории графов................................................... |
193 |
7.14.2 Постановка сетевой транспортной задачи............................................ |
197 |
7.14.3 Решение однородных систем с матрицей инциденций....................... |
199 |
7.14.4 Метод потенциалов для решения сетевой ТЗ....................................... |
200 |
7.14.5 Варианты СТЗ и родственные ей задачи .............................................. |
206 |
УПРАЖНЕНИЯ И ЗАДАЧИ………………………………………………………..213
ПРИЛОЖЕНИЯ........................................................................................................... |
228 |
|
1. |
Варианты контрольных заданий.......................................................................... |
228 |
2. |
Методические указания по выполнению контрольных заданий...................... |
247 |
3. |
Пример выполнения контрольной работы ......................................................... |
249 |
РЕКОМЕНДУЕМЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………..275

5
ВВЕДЕНИЕ
Задачей линейного программирования (ЗЛП) называется задача отыскания экстремума (максимума или минимума) линейной функции от нескольких переменных при линейных ограничениях на эти переменные.
Пример: Найти максимальное значение функции f (x1 ,x2 ) = 2x1 + 5x2
при следующих ограничениях на переменные x1 и x2 .
x1 + x2 ≤ 1277x1 − x2 ≤ 83
x1 ≥ 0,x2 ≥ 0
Приведенная задача есть ЗЛП максимизации от двух переменных с ограниченияминеравенствами (могут быть и ограничения-равенства). Линейная функция f называется функцией цели, или целевой функцией. Ограничения
x1 ≥ 0,x2 ≥ 0
называются ограничениями неотрицательности (или условиями неотрицательности), а система линейных неравенств и (или) уравнений называется системой ограничений ЗЛП. Запись ЗЛП с ограничениями-неравенствами выглядит следующим образом
f (x1 , x2 ) = 2x1 + 5x2 → max
x1 + x2 ≤127
7x1 − x2 ≤ 83 }
x1 ≥ 0, x2 ≥ 0 }
ЗЛП является удобной математической моделью для большого числа экономических задач (планирование производства, расходование ресурсов, раскрой материалов, транспортные перевозки и т.д.). Рассмотрим на примерах процесс построения математической модели (в виде ЗЛП на максимум или минимум) для ряда экономических задач.
1. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ДЛЯ ЭКОНОМИЧЕСКИХ ЗАДАЧ
Основа построения экономических моделей в виде ЗЛП - это, прежде всего, правильный выбор параметров экономической задачи (или некоторого процесса), через которые требуемая цель выражалась бы в виде линейной целевой функции, а ограничения на процесс записывались бы в виде системы линейных уравнений или неравенств.
1.1. Задача планирования производства продукции (ЗЛП на максимизацию).
Некоторое предприятие в течение планового периода выпускает 2 вида продукции, например, табуретки и стулья. При их производстве используются три вида ресурсов. Дан-
ные по их расходу на выпуск одного изде- |
|
|
|
|
|
|
|
|
|
Табуретка |
Стул |
Запас ресурса |
|
лия, запасы ресурсов, а также прибыль от |
|
|
|
|||
реализации единицы продукции приведе- |
|
Ресурс 1 |
4 |
6 |
24 |
|
|
Ресурс 2 |
|
3 |
2 |
12 |
|
ны в таблице. Требуется спланировать |
|
|
||||
количество выпускаемых табуреток и |
|
Ресурс 3 |
1 |
1 |
8 |
|
стульев таким образом, чтобы при данных |
|
Прибыль |
|
4 |
5 |
|
условиях производства полученная при- |
|
|
|
|
|
|

6
быль была максимальна. Итак, цель задачи - получение максимальной прибыли. Выберем в качестве параметров, характеризующих процесс планирования производства продукции, число выпускаемых табуреток (переменная x1) и выпускаемых стульев (переменная x2). Выразим через выбранные неизвестные суммарную прибыль от реализации всей продукции
f (x1 , x2 ) = 4x1 + 5x2
Она включает в себя прибыль от реализации всех табуреток ( 4x1) и выпускаемых стульев (5x2 ). Цель задачи (максимизация прибыли) запишется в виде
f (x1 , x2 ) = 4x1 + 5x2 → max
Перейдем к формулировке ограничений. Структура всех трех ограничений одинакова
РАСХОД РЕСУРСА ≤ ЗАПАС РЕСУРСА
Теперь остается выразить полный расход ресурса через выбранные неизвестные x1 и x2 . Так, расход ресурса первого вида на выпуск всех табуреток составит 4x1 единиц, а на выпуск всех стульев 6x2 соответственно (см. первую строку таблицы). В сумме это даст полный расход ресурса первого вида и ограничение примет вид линейного неравенства
4x1 + 6x2 ≤ 24
Аналогично запишутся ограничения по второму и третьему видам ресурсов 3x1 + 2x2 ≤ 12
x1 + x2 ≤ 8
Объединяя их в систему получим
4x1 + 6x2 ≤ 24
3x1 + 2x2 ≤ 12
x1 + x2 ≤ 8
Далее, исходя из смысла введенных переменных, (число производимых изделий не может быть отрицательным) на них необходимо наложить ограничения неотрицательности.
x1 ≥ 0, x2 ≥ 0
Окончательно выпишем математическую модель задачи в форме ЗЛП. f (x1, x2 ) = 4x1 + 5x2 → max
4x1 + 6x2 ≤ 24
3x1 + 2x2 ≤ 12
x1 + x2 ≤ 8 x1 ≥ 0, x2 ≥ 0
Полученная модель может изменяться за счет изменения как условий производства, так и условий реализации продукции. Например, при изменении условий реализации изменятся и коэффициенты в целевой функции. При изменении запасов ресурсов изменятся правые части в системе ограничений. При учете новых условий производства система ограничений дополнится новыми уравнениями или неравенствами.
После решения поставленной ЗЛП переменные x1 и x2 укажут плановое количество табуреток и стульев для получения максимальной прибыли, а разность между правой и левой частями каждого неравенства даст остаток ресурса каждого вида.

7
1.2. Задача о составлении оптимального рациона (ЗЛП на минимизацию)
Предположим, что в дневной рацион животных должны входить питательные вещества двух видов в количестве, заданном в таблице. Имеется возможность составлять рацион из кормов
|
Корм 1 |
Корм 2 |
Пит. в-в в рац. |
Пит. в-во 1 |
2 |
1 |
12 |
Пит. в-во 2 |
6 |
4 |
30 |
Цена корма |
5 |
2 |
|
двух видов, для которых задано содержание питательных веществ в единице корма и цена одной единицы каждого из видов кормов. При удовлетворении условий по необходимому содержанию питательных веществ в данном рационе требуется достичь его минимальной стоимости.
Пусть x1 и x2 - содержание в данном рационе единиц корма 1-го и 2-го вида соответственно. Общую стоимость дневного рациона запишем, используя цены на корма:
f (x1 , x2 ) = 5x1 + 2x2 → min Ограничения имеют следующую структуру:
содержание пит. веществ в рационе ≥ min кол-во пит. в-в.
Используя для записи левой части введенные неизвестные, получим
2x1 + x2 ≥126x1 + 4x2 ≥ 30
Добавив к полученным ограничениям условия неотрицательности (xi равно нулю, если корм i не используется в рационе), окончательно запишем ЗЛП.
f (x1, x2 ) = 5x1 + 2x2 → min
2x1 + x2 ≥126x1 + 4x2 ≥ 30
x1 ≥ 0, x2 ≥ 0
h В приведенных примерах все ограничения имеют вид линейных неравенств. Это, так называемые, нежесткие ограничения (ресурс может быть израсходован полностью, а может и частично). Однако можно ставить и жесткие ограничения в виде линейных уравнений. Так, в первом примере, требование полного использования ресурса 1-го вида приводит к ограничению: 4x1 + 6x2 = 24
h
2. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗЛП. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ЗЛП С ДВУМЯ ПЕРЕМЕННЫМИ И ОГРАНИЧЕНИЯМИ-НЕРАВЕНСТВАМИ.
Графическое решение ЗЛП с двумя переменными и системой ограничений в виде линейных неравенств состоит из 2-х этапов:
1.Построение на плоскости множества решений системы линейных неравенств, являющегося выпуклым многогранным множеством.
2.Выбор в построенном множестве точки х*(х1*, х2*), доставляющей целевой функции требуемое экстремальное (max или min) значение.

8
Коротко о необходимом математическом аппарате.
1)Множество точек, удовлетворяющих уравнению ax1 + bx2 = c геометрически есть прямая (см. рис.)
x1 |
|
ax1 +bx2 |
≤ c |
(c > 0) |
|
|
x2 |
2)Множество точек, удовлетворяющих линейному неравенству, представляет собой полуплоскость по одну сторону от прямой (включая саму прямую)
Способ выбора искомой полуплоскости. |
||
а) На плоскости выбирается точка с известными координатами, не лежащая на гра- |
||
ничной прямой |
|
|
б) Координаты выбранной точки подставляются в неравенство. |
||
Возможны только два случая: |
|
|
1. Получено верное числовое неравенство. |
|
|
|
|
x1 |
|
|
Полуплоскость |
В этом случае искомой полуплоскостью бу- |
|
содержит |
|
проверяемую |
|
дет та, в которой содержится выбранная точка. |
|
|
|
точку |
|
|
|
x2 |
x1 |
|
|
Полуплоскость |
2. |
Числовое неравенство - невер- |
выбранную |
||
точку |
|
ное. |
не содержит |
|
|
|
|
|
x2
Искомая полуплоскость не содержит выбранной точки.
|
9 |
x1 |
Множество |
|
решений |
|
системы из трех |
|
неравенств |
4. Нормальный вектор N прямой ax+by=f задается коэффициентами при неизвестных x и y , т.е. N= (a ; b)
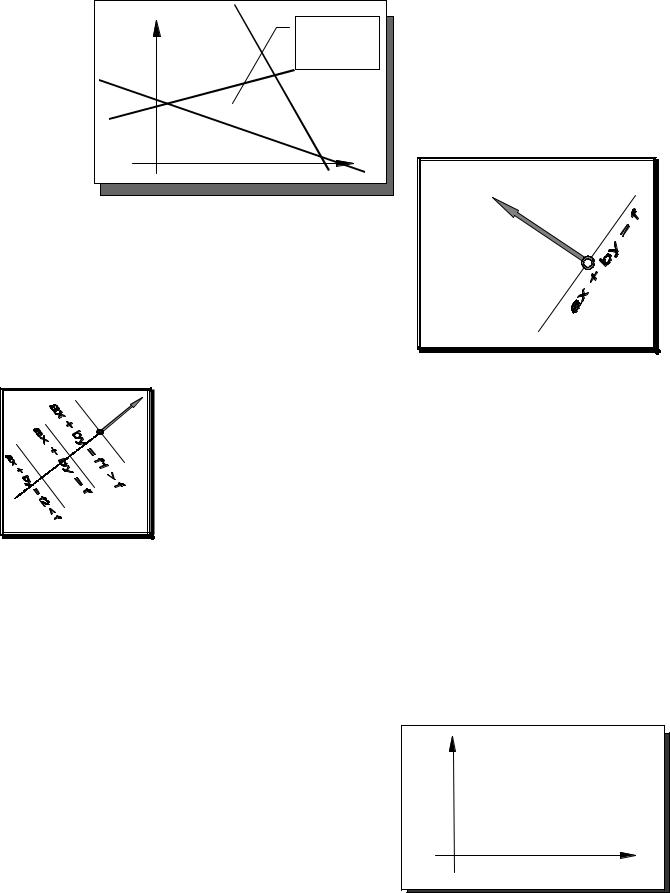
3. Множество точек, удовлетворяющих системе линейных неравенств представляет собой пересечение (общую часть) всех полуплоскостей, соответствующих каждому неравенству.
N
|
Свойство нормального вектора |
|
N |
а) При перемещении прямой (параллельно самой себе) в на- |
|
правлении вектора N значение f увеличивается. |
||
|
||
|
б) При перемещении прямой (параллельно самой себе) про- |
|
|
тив направления N значение f уменьшается. |
|
|
Разберем пример графического решения задачи максимиза- |
|
|
ции |
|
|
прибыли, сформулированной выше. |
|
|
f (x1, x2 ) = 4x1 + 5x2 → max |
4x1 + 6x2 ≤ 24
3x1 + 2x2 ≤ 12
x1 + x2 ≤ 8 x1 ≥ 0, x2 ≥ 0
1. Изобразим на плоскости систему координат
x2 |
x1 |
0 |
