
Зад лин прогр и мет их решения 16 12 08
.pdf
|
10 |
|
2. Рассмотрим ограничения неотрицательности. |
||
|
|
а) Неравенство x1 ≥ 0 определяет |
x1 |
|
полуплоскость, в которой все точки |
x2 |
|
имеют неотрицательную первую ко- |
{ x1 ≥ 0 |
|
ординату. |
x1 |
|
|
|
|
|
0 |
|
|
x1 |
|
|
x2 |
|
|
{ x2 ≥ 0 |
|
б) Неравенству x2 ≥ 0 соответ- |
|
|
|
|
|
ствует полуплоскость, где вторая ко- |
|
x1 |
ордината каждой точки неотрица- |
|
|
тельна. |
0 |
|
|
x1 |
|
в) Системе неравенств соответ- |
|
ствует 1-я четверть. |
|
x2 |
|
|
|
|
|
x1 ≥ 0 |
|
|
x2 ≥ 0 |
|
|
|
x1 |
|
0 |
|
|
|
|
|
|
hВ дальнейшем, если заданы |
|
ограничения неотрицательности, все построения проводятся в 1-ой четвертиh |
|||||
|
|
|
1-ое неравенство |
|
|
3. Строим множество точек, соответст- |
x1 |
|
|||
x2 |
|
||||
вующее множеству решений системы ограни- |
|
||||
|
|
||||
чений. |
|
|
4x1 + 6x2 |
= 24 |
|
Берем первое неравенство |
|
|
|
||
{4x1 + 6x2 ≤ 24 |
|
|
4 |
||
и заменим его уравнением |
|
|
|
||
{4x1 + 6x2 = 24 |
|
0 |
6 |
||
|
|
|
|
||
Строим |
прямую, |
соответствующую |
этому |
|
x1 |
|
|
||||
уравнению. |
|
|
|
(I) |
|
|
|
|
|
||
(Если она не проходит через начало коорди- |
|
|
|||
нат, то удобнее всего строить эту прямую по |
|
|
|||
точкам пересечения с осями координат). |
|
|
|
||
11
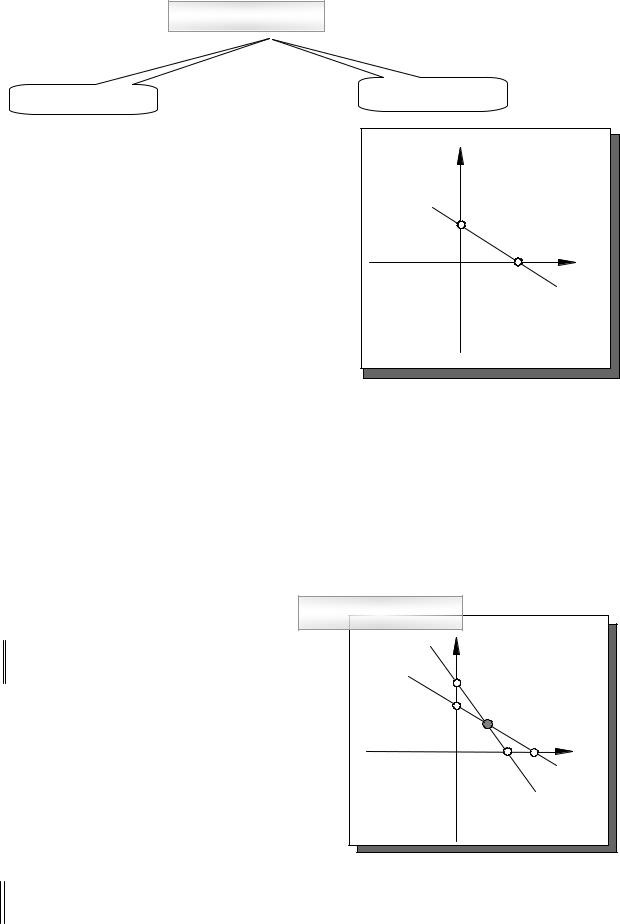
Точка пересечения
x |
= 0 |
|
|
x |
= 0 |
1 |
|
|
|
1 |
|
4 0 + |
6x |
2 = 24 |
x2 = 4 |
||
С осью ОХ2
Построенная прямая разбивает плоскость на 2 полуплоскости. Для выбора полуплоскости, соответствующей нашему неравенству, возьмем на плоскости точку с известными координатами, не лежащую на прямой (пусть это будет точка (0,0) - начало координат). Подставим координаты этой точки в неравенство
{4 0 + 6 0 ≤ 24 , {0 ≤ 24 Получилось верное числовое неравенство. Зна-
чит полуплоскость содержит выбранную для проверки точку (в данном случае - начало координат).
x |
= 0 |
|
x |
|
= 0 |
2 |
|
|
|
2 |
|
4x1 + 6 0 = 24 |
x1 = 6 |
||||
С осью ОХ1 |
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
A |
|
|
|
|
|
0 |
B |
|
|
x1 |
|
|
|
|
|
|
|
|
|
(I) |
|
|
hЗаметим, что для проверки не обязательно брать начало координат. Главное, чтобы точка не лежала на прямой и имела известные координаты. Например, возьмем точку М с координатами (8,0). Подставляем в неравенство
{4 8 + 6 0 ≤ 24 32 ≤ 24 Неравенство неверное. Значит полуплоскость не содержит точки М, т.е. опять определяется та же полуплоскость.h
Таким образом, в совокупности с первой четвертью текущее множество решений представляет собой треугольник ОAB. Далее аналогично строятся полуплоскости, соответствующие остальным неравенствам, и пересекаются с текущим множеством решений.
2-е неравенство
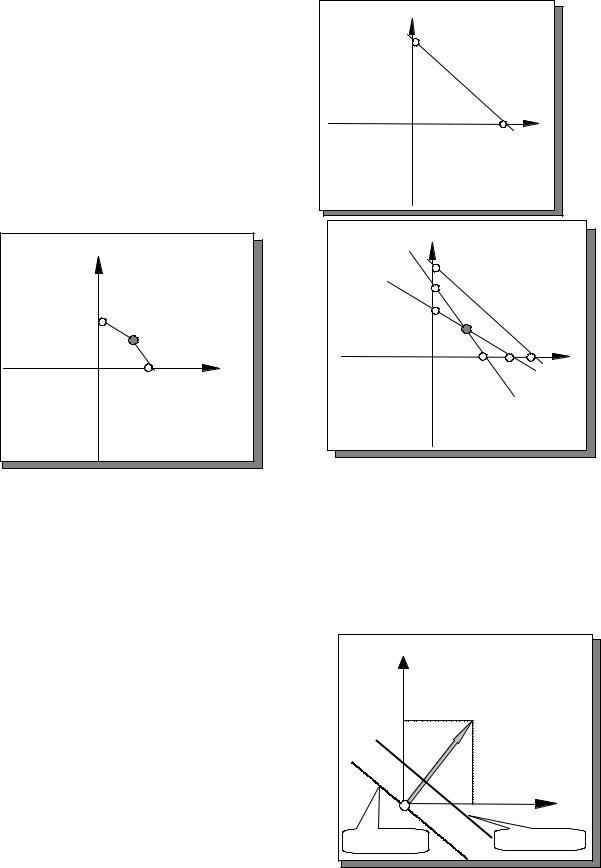
3x1 + 2x2 ≤12 3x1 + 2x2 =12 x1 = 0 x2 = 0
x2 = 6 x1 = 4
Точка для проверки О(0,0) 3 0 + 2 0 ≤12 0 ≤12
Верное неравенство. Полуплоскость содержит точку О. Пересекаем ее с предыдущим множеством. Получаем четырехугольник OAMD.
3-е неравенство
x1 + x2 ≤ 8 x1 + x2 = 8 x1 = 0 x2 = 0
x2 = 8 x1 = 8
2-ое неравенство |
|
x1 |
|
x2 |
|
|
C |
A |
M |
|
|
|
B |
0 |
D |
|
x1 |
|
(I) |
12
Подставляя в неравенство точку начала координат, убеждаемся, что полуплоскость содержит эту точку. При пересечении с предыдущим множеством решений приходим к выводу, что четырехугольник OAMD целиком содержится в данной полуплоскости.
hЭтот факт свидетельствует о том, что в данной задаче последнее ограничение не существенно и может быть либо отброшено, либо изменено за счет уменьшения запаса ресурса третьего видаh
x2 |
|
A |
M |
|
x1 |
0 |
D |
8 |
|
|
|
|
x2 |
|
|
|
|
|
|
8 |
x1 |
|
0 |
|
(III) |
|
|
|
|
|
|
|
x2 |
|
|
|
|
(II) |
E |
|
|
|
|
|
|
|
|
C |
|
|
|
|
A |
|
|
|
|
|
M |
|
F |
x1 |
|
|
|
||
0 |
D |
B |
(III) |
|
|
|
|
|
|
|
|
(I) |
|
|
Окончательно множество решений ЗЛП представляет собой четырехугольник OAMD.
4. Займемся отысканием в множестве решений точки, которая доставляет максимум целевой функции
f = 4x1 + 5x2
(эта точка будет соответствовать оптимальному решению)
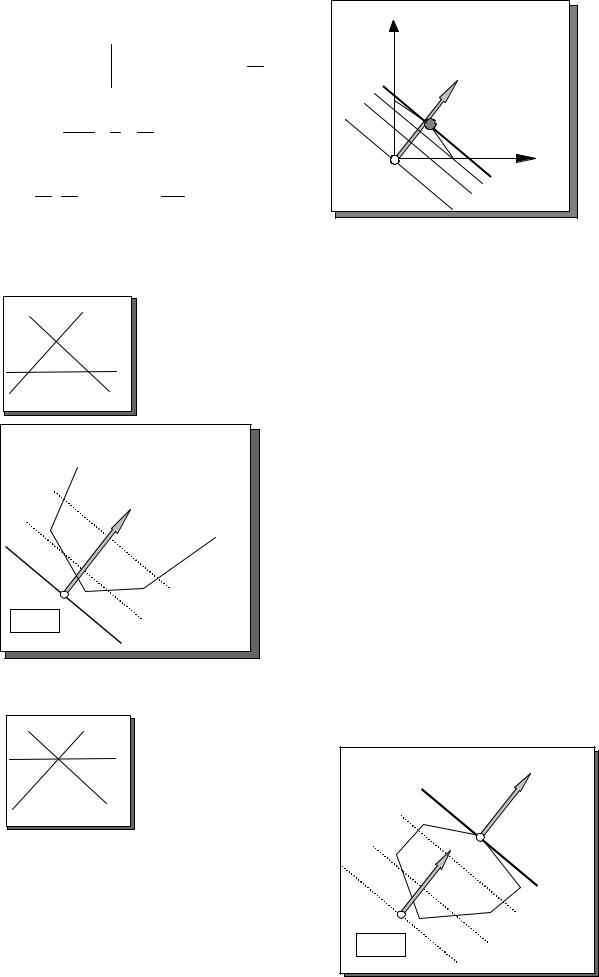
а) Для этого построим нормальный вектор N=(4,5). Если придать f какое-либо конкретное значение f0, то прямая будет проходить перпендикулярно N. (При f=0 прямая проходит через начало координат).
б) Перемещая прямую в направлении N (задача на MAX!!!), по которому значение целевой функции возрастает, находим последнюю точку пересечения прямой и множества решений. Эта точка и будет искомым оптимальным решением. Определяем ее компоненты как координаты точки пересечения 1-й и 2-й прямых
x2 |
|
|
N |
|
x1 |
4x1+5x2=0 |
4x1+5x2=f0>0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
3x1 + 2x2 =12 3 |
5x1 =12 x1 |
= |
12 |
|
|
||||||||||||
− |
|
|
|
|
|
|
|
|
|
|
||||||||
|
4x1 + 6x2 = 24 |
|
|
|
|
|
|
5 |
|
N |
||||||||
x2 = |
|
− |
3 12 |
|
|
1 |
= |
12 |
|
|
|
f = 0 |
X* |
|||||
12 |
5 |
|
2 |
|
5 |
|
|
|
|
x1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
* |
= |
12 |
12 |
|
|
|
f (x |
* |
) = |
108 |
|
|
|
f = f (x*) |
|||
|
|
, |
|
, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
5 |
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
Возвращаясь к исходной экономической задаче, можно заключить, что наиболее выгодно выпускать табуретки и стулья в одинаковом количестве.
Проиллюстрируем теперь различные случаи разрешимости и неразрешимости ЗЛП.
ЗЛП неразрешима (не имеет оптимального решения)
а) Из-за несовместности системы ограничений. Т.е. система не имеет ни одного решения.
N |
MAX |
ЗЛП разрешима |
б) Из-за неограниченности целевой функции на множестве решений. (В этом случае множество решений обязательно неограничено). Другими словами при решении ЗЛП на max значение целевой функции стремится к бесконечности, а в случае ЗЛП на min - к минус бесконечности.
Вектор N направлен в сторону неограниченности множества решений (при решении - задачи на MAX). Поэтому прямую можно перемещать до бесконечности, не достигнув последней точки пересечения.
а) Множество решений состоит из одной точки. Она же и является оптимальной.
б) Единственное оптимальное решение ЗЛП
Прямая, соответствующая целевой функции в предельном положении пересекается с множеством решений в одной точке.
N |
X* |
MAX |
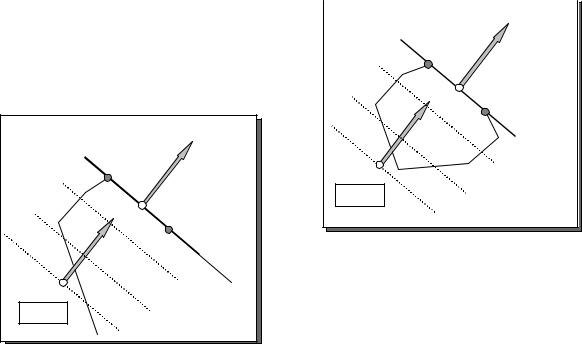
14
в) Оптимальное решение ЗЛП не единственно |
|
|
N |
||
|
||
Вектор N перпендикулярен к одной из сторон мно- |
|
|
жества решений. В этом случае оптимальной являет- |
A |
|
ся любая точка на отрезке АВ |
|
|
B |
|
N |
|
A |
|
MAX |
|
M |
MAX |
Здесь оптимальными решениями являют- |
|
|
|
ся точка А и любая точка луча АМ. |
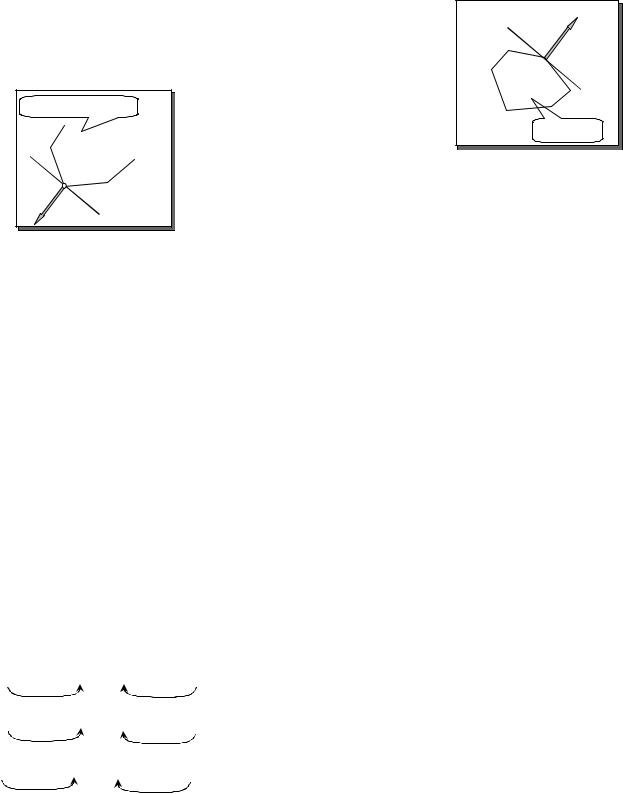
Графически также могут быть решены ЗЛП и с большим числом переменных, если их удается свести к ЗЛП с 2-мя переменными и ограничениями-неравенствами. Например, ЗЛП.
f = x1 + x2 + x3 + x4 + x5 → max
2x1 + 4x2 + 5x3 = 12 |
||||||
(*) 5x |
− x |
2 |
− 2x |
4 |
= 8 |
|
|
1 |
|
|
|
||
|
|
+10x2 + 7x5 = 70 |
||||
7x1 |
||||||
x1 , x2 , x3 , x4 , x5 ≥ 0
Путем отбрасывания переменных x3 , x4 , x5 из системы уравнений, замены их неравенства-
ми и выражения отбрасываемых переменных в целевой |
функции через x1 и x2 , задача мо- |
||||||||||||||||||||
жет быть приведена к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f = x |
+ x |
|
+ |
1 |
(12 − 2x |
− 4x |
|
)− |
1 |
(8 − 5x |
+ x |
|
)+ |
1 |
(70 − 7x |
−10x |
|
)→ max |
|||
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
2 |
|
|
5 |
|
1 |
|
2 |
2 |
1 |
|
2 |
7 |
1 |
|
2 |
|
||
2x1 + 4x2 |
≤ 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(**) 5x |
− x |
2 |
≥ 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7x |
+10x |
2 |
≤ 70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 , x2 ≥ 0
После графического решения (**) x3 , x4 , x5 определяются из ( )
15
3. СИМПЛЕКС-МЕТОД ДЛЯ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
3.1.Предварительные сведения
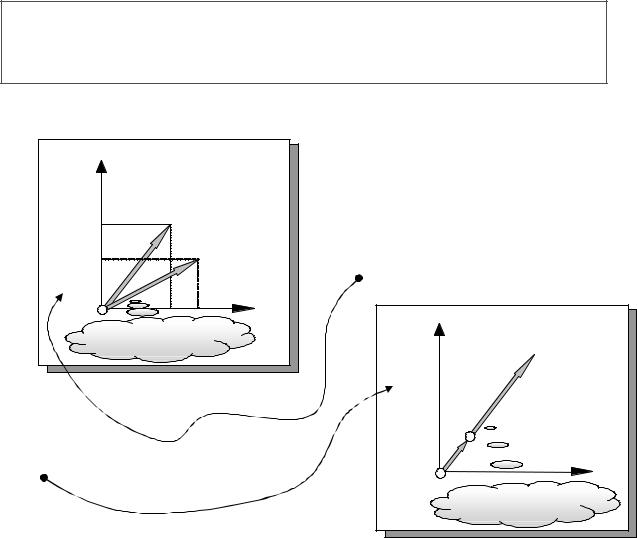
Из предыдущего раздела мы знаем, что множество решений ЗЛП представляет собой выпуклое многогранное множество. Оно может быть или ограниченным (в этом случае его называют выпуклым многогранником. Простейший выпуклый многогранник называется симплексом )
НЕОГРАНИЧЕННОЕ ВЫПУКЛОЕ |
МНОГОГРАННОЕ МНОЖЕСТВО |
X* |
или неограниченным.
Далее, из теории линейного
 X*
X*
ВЫПУКЛЫЙ
МНОГОГРАННИК
программирования
известны утверждения:
1. Если ЗЛП имеет оптимальное решение, то оно достигается в вершине множества решений.
2. Точка X , представляющая вершину множества решений ЗЛП, является базисным решением системы ограничений ЗЛП, записанной в виде системы линейных уравнений.
Для того, чтобы пояснить смысл понятия “базисное решение”, рассмотрим способ записи ЗЛП с ограничениями-равенствами. Возьмем пример из раздела 1, касающийся планирования выпуска продукции (задача на max).
f (x1 , x2 ) = 4x1 + 5x2 → max
4x1 + 6x2 ≤ 243x1 + 2x2 ≤ 12
x1 + x2 ≤ 8
x1 ≥ 0, x2 ≥ 0
Система ограничений здесь записана в виде системы линейных неравенств. Превратим каждое из неравенств в уравнение путем введения в левую часть дополнительных переменных, равных разнице между правой и левой частью неравенства.
Например. |
|
|
1-е неравенство |
дополнительная переменная |
1-е уравнение |
{4x1 + 6x2 ≤ 24 |
x3 = 24 − (4x1 + 6x2 ) ≥ 0 |
{4x1 + 6x2 + x3 = 24 |
2-е неравенство |
дополнительная переменная |
2-е уравнение |
{3x1 + 2x2 ≤ 12 |
x4 = 12 − (3x1 + 2x2 ) ≥ 0 |
{3x1 + 2x2 + x4 =12 |
3-е неравенство |
дополнительная переменная |
3-е уравнение |
{x1 + x2 ≤ 8 |
x5 = 8− (x1 + x2 ) ≥ 0 |
{x1 + x2 + x5 = 8 |
Окончательно получаем ЗЛП с пятью переменными
16
f = 4x1 |
+5x2 |
|
|
→ max |
||
4x1 + 6x2 + x3 |
|
= 24 |
||||
|
|
|
|
+ x4 |
|
=12 |
3x1 + 2x2 |
|
|||||
|
x |
+ x |
2 |
+ x |
5 |
= 8 |
|
1 |
|
|
|
||
xi ≥ 0 (i 1:5) ( * )
“Заплатить” за ограничения-равенства пришлось увеличением числа неизвестных (на число введенных дополнительных переменных x3 , x4 , x5 ). Отсутствие дополнительных
переменных в целевой функции означает, что они входят туда с коэффициентами, равными нулю. Каждой переменной в системе ограничений соответствует столбец коэффициентов.
Например,
|
4 |
|
6 |
|
1 |
|
0 |
|
0 |
|||||
x1 ~ |
|
|
x2 ~ |
|
|
x3 ~ |
|
|
x4 ~ |
|
|
x5 ~ |
|
|
3 , |
2 , |
0 , |
1 , |
0 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
0 |
|
0 |
|
1 |
|||||
Если столбцы коэффициентов, соответствующие положительным значениям переменных, в решении ЗЛП образуют базис (они линейно независимы и число их равно числу уравнений), то такое решение называется базисным.
Если один из векторов набора можно выразить через остальные, то это набор линейнозависимых векторов. В противном случае вектора набора линейно независимы.
x2 |
A |
B |
x1 |
Вектора А и В линейно |
независимы |
Здесь указанное равенство возможно
|
1 |
3 |
A = |
, |
B = , |
|
3 |
1 |
Ни при каких числовых коэффициентах α |
||
невозможно равенство |
|
|
A =α B |
|
|
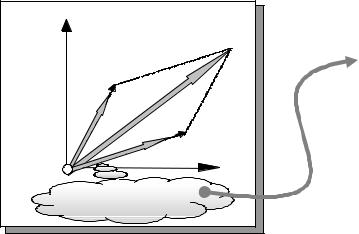
x2 |
|
|
|
|
B=2 |
A |
|
|
|
|
x1 |
|
Вектора А и В линейно |
|
|
|
зависимы |
|
|
|
|
|
|
17 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
С =α1 A +α2 B |
α1A |
|
C |
|
|
|
|
|
|
|
т.к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
α2B |
x1 |
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
Вектора А, B и C линейно |
|
|
|
|
|
|
|
|
|
|
|
зависимы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, решение ЗЛП ( ) |
|||||
x1 |
= x2 = 0, |
x3 = 24, |
x4 =12, |
x5 = 8 |
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
X = (0, 0, 24, 12, |
|
8) |
|
|
|
|||||
будет базисным, т.к. столбцы, отвечающие положительным переменным x3 , x4 , x5 |
|||||||||||
|
1 |
|
0 |
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
1 |
|
|
|
||
образуют, так называемый, единичный базис. |
|
|
|
|
|
||||||
(Во-первых, эти столбцы линейно независимы, т.е. ни один из них нельзя выразить в виде |
|||||||||||
линейной комбинации остальных, и, во-вторых, их число равно числу уравнений). |
|||||||||||
С другой стороны, решение |
|
|
|
|
|
|
|
|
|
|
|
|
X = (1, |
1, |
14, |
7, 6) |
|
|
|
||||
не является базисным, т.к. число столбцов, отвечающих положительным неизвестным |
|||||||||||
больше числа уравнений. |
|
|
|
|
|
|
|
|
|
|
|
Еще один пример небазисного решения |
|
|
|
|
|
||||||
|
2x − 4x |
|
+ x |
|
|
|
= 7 |
|
|||
|
|
1 |
|
2 |
|
|
3 |
|
|
|
|
|
x1 − 2x2 |
|
|
|
+ x4 |
|
=1 |
|
|||
|
− x + 2x |
2 |
|
|
|
+ x |
5 |
= −1 |
|
||
|
|
1 |
|
|
|
|
|
|
|
||
|
|
xi |
≥ 0 |
|
|
(i 1:5) |
|
|
|
||
Решение |
X = (3, |
1, 5, |
0, |
|
0) |
|
|
|
|
||
не является базисным, т.к., хотя число положительных неизвестных и равно числу |
|||||||||||
уравнений, однако, отвечающие им столбцы |
|
|
|
|
|
|
|||||
|
|
А1 |
|
|
|
|
|
А2 |
|
|
|
|
А3 |
|
|
|
2 |
|
|
|
|
− 4 |
|
|
|
1 |
|||
x |
~ |
1 |
, |
x |
2 |
~ |
− 2 , |
x |
3 |
~ |
0 , |
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
0 |
|||
линейно зависимы, (хотя бы потому, что второй столбец выражается через первый, т.е.
А2 = -2А1
или

18
|
− 4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
= −2 |
|
|
|
|
|
|
|
|
− 2 |
|
1 |
). |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
−1 |
|
|
|
|
|
Теперь достаточно просто |
оценить |
число |
базисных |
решений |
ЗЛП |
с m |
||||
ограничениями относительно n |
переменных |
|
|
(или, что тоже |
самое, |
число |
вершин |
|||
множества решений). Так как столбцов коэффициентов в системе n штук, а любой базис состоит из m столбцов, то максимальное число базисных решений (при условии, что любое сочетание из m столбцов образует базис и значения переменных, отвечающие им, положительны) будет равно числу сочетаний из n элементов по m элементов. Или, иначе,
|
|
|
|
|
m |
= |
n! |
|
|
|
|
|
|
||||
|
|
Число вершин множества |
|
|
||||
|
|
|
|
|
|
|||
|
|
решений ЗЛП |
|
≤ |
Cn |
|
|
|
|
|
|
m!(n − m)! |
|||||
|
|
|
|
|||||
|
|
|
|
( n! = 1· 1· 1·…(n-1)·n ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так, для нашего примера (n = 5, m = 3) множество решений содержит
C |
3 |
= |
5! |
|
= |
1 2 3 4 5 |
=10 вершин |
|
5 |
|
|
|
|
||||
3!(5−3)! |
|
1 2 3 1 2 |
||||||
|
|
|
|
|
||||
Казалось бы, что самым простым методом решения ЗЛП является перебор всех базисных решений или вершин (ведь мы знаем, что оптимальное решение находится среди них!). И, действительно, в случае нашего примера нетрудно десять раз решить систему из трех уравнений с тремя неизвестными (две переменные, не отвечающие базисным столбцам, полагаются равными нулю). Однако уже для такой средней ЗЛП, которая имеет 20 переменных и 10 ограничений, оценка для числа базисных решений равна
C |
10 |
= |
20! |
|
=184756 |
||
|
|
|
|||||
20 |
10!(20 −10)! |
||||||
|
|
|
|||||
Как говорится: “Хотя и конечно, но очень велико!”.
3.2. Геометрическая идея симплекс-метода
Идея состоит в том, чтобы вершины множества решений (базисные решения) перебирать направленно.
1. Пусть мы находимся в некоторой вершине множества решений x0 (имеем
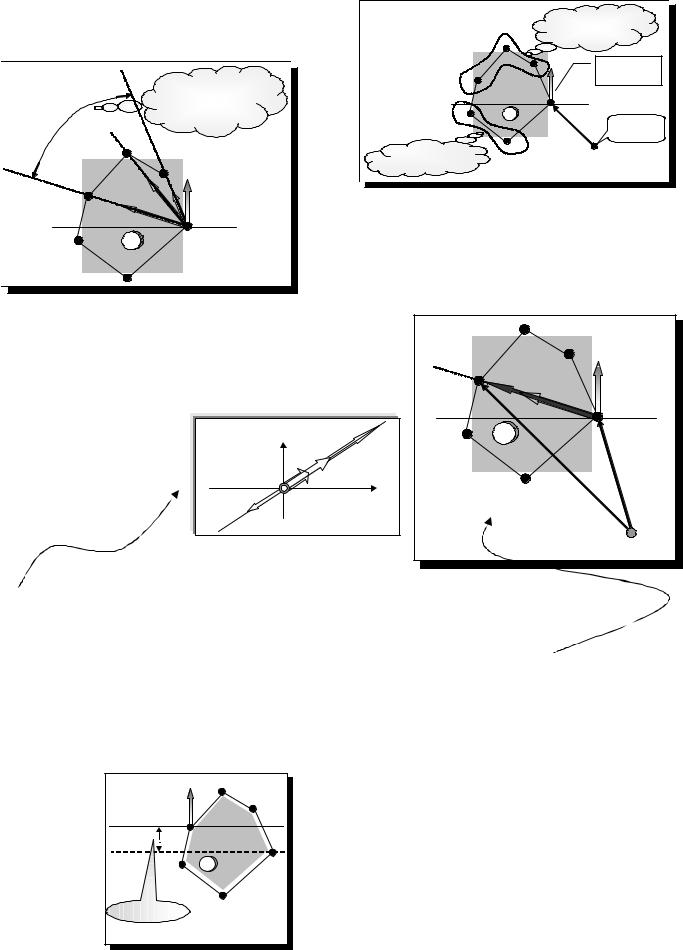
некоторое базисное решение ЗЛП). Для определенности будем рассматривать ЗЛП на max. Тогда все вершины разделятся на две части: “лучшие”, чем x0 (значение целевой функции в них больше, чем f( x0 )=f0) и “худшие”, чем x0 (с меньшим, чем f0 значением целевой функции (см. рис.)). В симплекс-методе каждый раз осуществляется переход к одной из “лучших” вершин (вершины “худшие”, чем x0, как бы заранее отсекаются). Все начинается с того, что для текущей вершины проверяется условие (критерий) оптимальности (т.е. имеются ли вершины “лучшие”, чем x0 ). Если таких вершин нет, то имеющееся решение оптимально.
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вершины, "лучшие" |
|
|
|
|
|
|
|
|
|
|
|
чем X0 |
(f > f0) |
|
|
|
|
|
|
|
|
X4 |
|
|
|
|
|
|
|
|
|
|
|
|
X5 |
|
Направление |
|
|
|
|
|
|
|
|
|
|
возрастания f |
|
|
|
|
|
|
|
|
X3 |
Мн-во |
|
||
|
|
|
Конус возможных |
|
|
|
|
||||
|
|
|
|
|
|
Решений |
|
|
|||
|
|
|
направлений |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ЗЛП |
f = f0 |
|
||
|
|
|
улучшения решения X0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
X2 |
1 |
X0 |
|
Начало |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
координат |
|
X4 |
|
|
|
|
|
|
|
X1 |
|
|
|
|
|
|
|
|
Вершины, "худшие" |
|
|
|
0 |
|
|
|
X5 |
|
|
|
чем X0 |
(f < f0) |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-Z2 |
-Z3 |
|
|
|
|
|
|
|
|
X3 |
|
|
|
|
|
|
|
|
|
|
|
|
-Z1 |
|
|
|
|
2. В противном случае определяются |
|||||
|
|
|
|
|
|
||||||
X2 |
2 |
|
X0 |
|
|
направления на “лучшие” вершины (здесь -z1, - |
|||||
|
|
|
|
||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
z2, -z3), которые |
образуют |
конус |
возможных |
||
|
|
X1 |
|
|
|
направлений улучшения текущего решения x0. |
|||||
|
|
|
|
|
|
||||||
3. |
Далее |
выбирается |
одно |
из |
направлений |
|
X4 |
|
|
||
улучшения |
решения |
(например -z1 |
). |
С помощью |
|
|
|
||||
|
|
|
X5 |
N |
|||||||
положительного числового коэффициента θ вектор -z1 |
|
|
|
|
|||||||
|
|
|
|
|
|||||||
растягивается (или сжимается) таким образом, чтобы |
X3 |
- θZ1 |
|
|
|||||||
вектор -θz1 “упирался” в “лучшую” вершину (здесь x3). |
|
-Z1 |
|
|
|||||||
|
|
|
|
|
|||||||
2 Z |
X2 |
3 |
X0 |
|
|||
Z |
|
|
|
0.5 Z |
|
|
X1 |
- Z |
|
|
|
|
|
|
0 |
Умножение вектора на число θ >1 геометрически представляет растяжение вектора в θ раз, если же θ <1, то умножение на θ сжимает вектор в θ раз (см. рис.)
После выбора переход к “лучшей” вершине совершается по правилу (см.рис.) x3 = x0 − θ z1
Теперь в качестве текущего решения имеем вершину x3 , в которой значение целевой функции больше, чем в предыдущей вершине x0.
f (x3 ) = f1 > f0 = f (x0 )
|
N |
X4 |
|
|
|
|
X5 |
f = f1 |
|
|
|
|
X3 |
|
|
f = f0 |
X2 |
1 |
X0 |
|
|
||
|
|
|
X1 |
f = f1-f0 |
|
|
|
“Скачок” целевой функции в сторону увеличения равен f . Таким образом, мы опять
пришли к случаю , но текущее значение
целевой функции увеличилось. Описанные шаги повторяются до тех пор, пока не будет достигнута оптимальная вершина (в данном случае это x4). Так как число вершин конечно и целевая функция каждый раз не убывает, то через конечное число шагов будет получено оптимальное решение ЗЛП.
