Зад лин прогр и мет их решения 16 12 08
.pdf
111
7.10. Пары двойственных задач. Теоремы двойственности
Рассмотрим ЗЛП в общей форме записи ( M1 , M 2 M , M1 M 2 = M , N1 , N2 N ,
N1 N2 = N )
f (X ) = C[N] X[N] → max
A[M1 , N] X[N] ≤ b[M1 ] A[M 2 , N] X[N] = b[M 2 ]
X[N1 ] ≥ 0[N1 ]
X[N2 ] >< 0[N2 ]
С ней тесно связана некоторая другая ЗЛП, которая носит название ЗЛП двойственной к данной.
g(Y) = Y[M ] b[M ] → min
Y[M ] A[M, N1 ] ≥ C[N1 ]
Y[M ] A[M , N2 ] = C[N2 ]
Y[M1 ] ≥ 0[M1 ]
Y[M 2 ] >< 0[M 2 ]
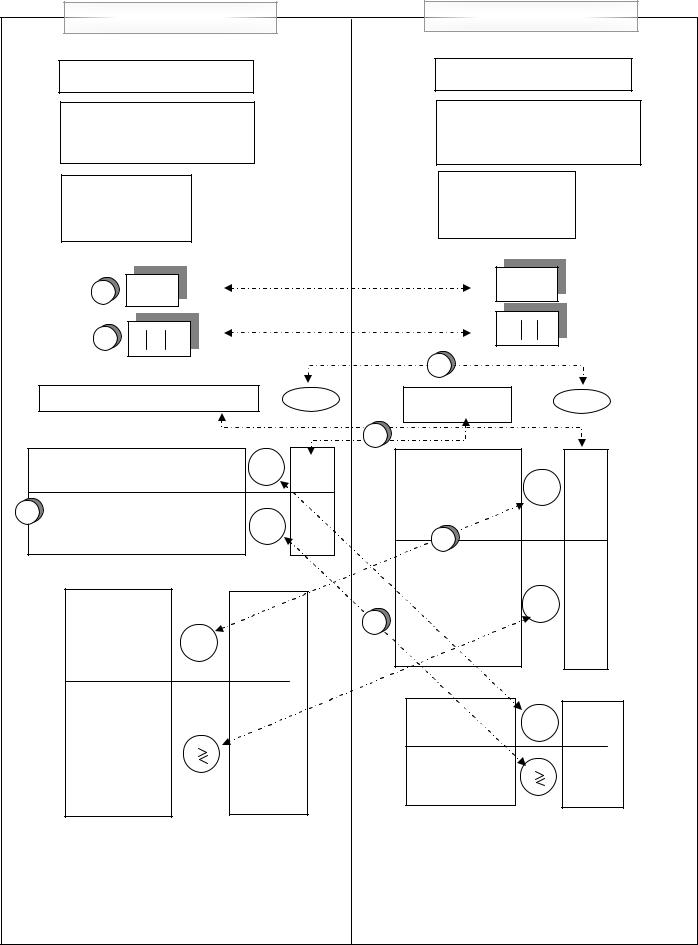
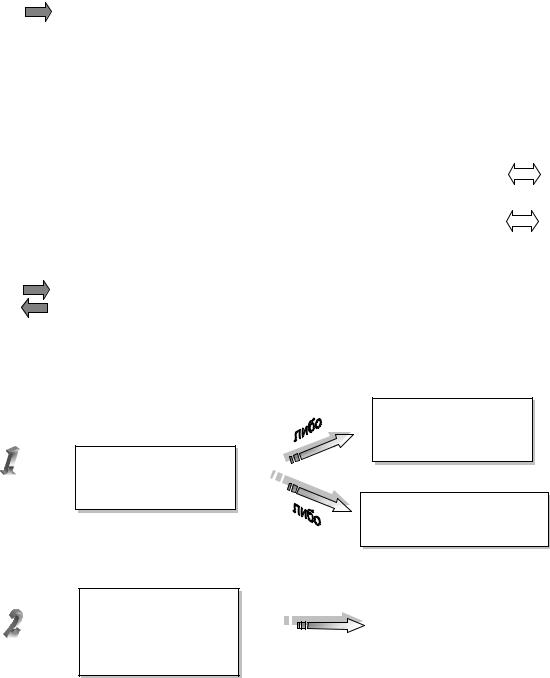
Построение двойственной задачи сводится к следующей схеме:
1-2Число переменных в двойственной задаче равно числу ограничений в исходной, а число ограничений в двойственной равно числу переменных в исходной.
3 В двойственной задаче меняется вид экстремума (max на min и наоборот).
4 Векторы правой части ( в[M] ) и коэффициентов целевой функции (C[N]) в двойственной задаче меняются местами: первый становится вектором коэффициентов целевой функции, а второй - вектором правой части в системе ограничений.
5Левая часть системы ограничений строится по транспонированной матрице AT [N, M ] (строки в A[M , N] становятся столбцами и наоборот), которая умножается на вектор переменных двойственной задачи Y[M ]
6Знаки в системе ограничений двойственной задачи определяются знаками ограничений неотрицательности в исходной задаче:
- ограничения неотрицательности на переменные X[N1 ] дают нежесткие ограничения с номерами из N1 (типа ≥ для задачи на min и ≤для задачи на max); - отсутствие ограничений неотрицательности на переменные X[N2 ] определяет
жесткие ограничения (равенства) с номерами из N2 . И, наоборот,
- нежесткие ограничения с номерами из M1 дают ограничения неотрицательности на
переменные Y[M1 ];
- жесткие ограничения с номерами из M 2 не накладывают условий неотрицательности на переменные Y[M 2 ](в дальнейшем запись Y >< 0 будем опускать).
hДвусторонние стрелки на схеме показывают, что ее можно применять в обе стороныh
|
|
|
|
|
|
|
|
|
|
|
|
112 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исходная задача (I) |
|
|
|
|
|
Двойственная задача (II) |
|
|
||||||||
|
|
f (x) = c[N] x[N] → max |
|
|
|
g(y) = y[M ] b[M ] → min |
|
||||||||||||||
|
|
A[M |
1 , N] x[N] ≤ b[M1 ] |
|
|
|
|
T |
[N1 , M ] |
y[M ] ≥ c[N1 ] |
|||||||||||
|
|
|
|
|
A |
|
|||||||||||||||
|
|
|
A[M |
|
, N |
] x[N] = b[M |
|
] |
|
|
|
|
|
[N |
|
, M ] y[M ] = c[N |
|
] |
|||
|
|
|
2 |
2 |
|
|
|
AT |
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x[N1 ] ≥ 0[N1 ] |
|
|
|
|
|
y[M1 ] ≥ 0[M1 ] |
|
|
|
||||||||||
|
|
x[N2 ] ≥≤ 0[N2 ] |
|
|
|
|
|
y[M 2 ] ≥≤ 0[M 2 ] |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Переменные |
|
|
|
|
y[M ]] |
|
|
|
||
|
|
|
|
1 |
|
|
x[N] |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Число ограничений |
|
|
|
|
N |
|
|
|
||
|
|
|
|
2 |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
max |
b |
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
A: |
|
A[M |
, N] x[N] |
|
|
≤ |
b[M1 ] |
A: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
AT [N |
, M ] y[M ] |
≥ |
c[N ] |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
5 |
A[M 2 , N] x[N] |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
b[M2 ] |
5 |
|
|
|
|
|
|
|
c |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
AT [N |
, M ] y[M ] |
= c[N2 ] |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x[N1] |
≥ |
|
|
0 [N1 ] |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y[M1 ] |
|
|
≥ 0 [M1 ] |
|
|
|||
|
|
|
|
x[N2 ] |
|
|
|
0 [N2 ] |
|
|
|
|
|
|
|
0 [M 2 ] |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
y[M 2 ] |
|
|
|
|
|
|||
114
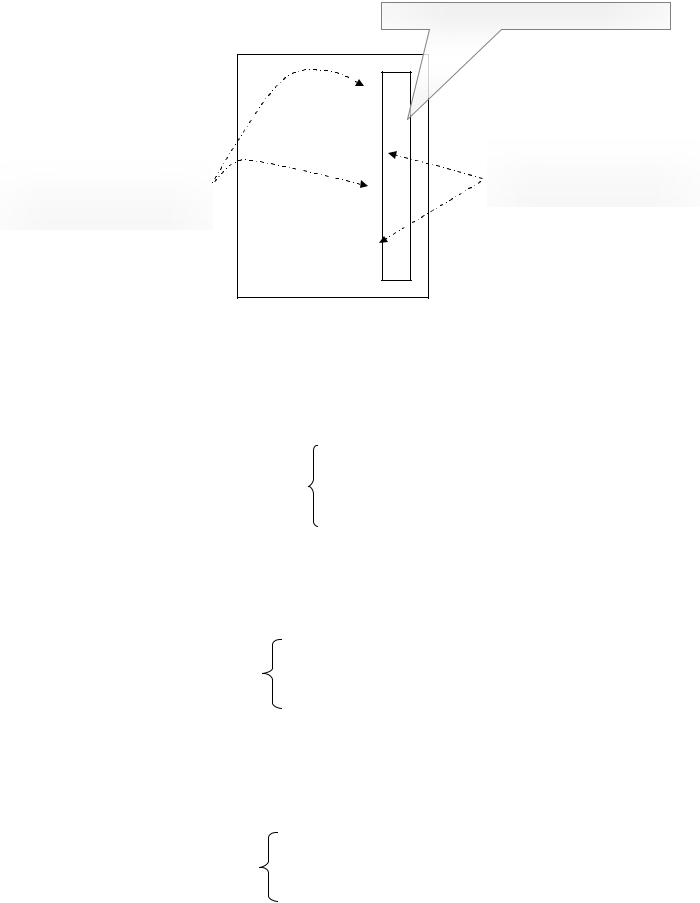
Это вектор правой части двойственной задачи
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2y + y |
2 |
=7 |
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y + y ≥3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Ограничения неотрицательности |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
Ограничений неотрицательности |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
на х2 и х4 дают нежесткие 2-е и |
||
на х1 и х3 нет. Значит 1-е и |
|
|
|
|
|
|
|
|
|
|
|
|
|
4-е ограничения (вида ≥ , т.к. |
|
|
|
|
|
|
4y − y |
|
|
= −1 |
|
|
|
задача на min). |
|||
3-е ограничения - жесткие. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− y + y ≥ 2 |
|
|
|
|
||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первое ограничение в исходной задаче имеет вид неравенства (нежесткое), поэтому y1 ≥ 0
Жесткое ограничение (2-ое) не дает ограничения неотрицательности на y2 . Окончательно запишем двойственную задачу
g = 9y1 + 7y2 |
→ min |
|
2y1 |
+ y2 |
= 7 |
y1 |
+ y2 |
≥ 3 |
4y1 |
− y2 |
= −1 |
− y1 |
+ y2 ≥ 2 |
|
|
|
|
|
y1 |
≥ 0 |
|
|
|
|
|
|
2 |
f = 5x1 |
+ 4x2 |
+ 2x3 → max |
|
|
|
|
||||
|
x1 + 2x2 + x3 ≤ 6 |
|
1 |
2 |
1 |
||||||
|
2x1 + x2 + 4x3 ≤ 7 |
A = |
2 |
1 |
4 |
||||||
|
2x + 3x |
|
+ 5x |
|
≤12 |
|
|
|
|
||
|
2 |
3 |
|
|
3 |
|
|||||
|
1 |
|
|
|
|
|
2 |
5 |
|||
|
xi |
≥ 0 , |
i 1:3 |
|
|
|
|
||||
ЗЛП в симметричной форме имеет три переменные и три ограничения. Двойственная задача будет такой же размерности.
g = 6y1 + 8y2 |
+ 12y3 → min |
|
|
|
|
|
|
y1 + 2y2 |
+ 2y3 ≥ 5 |
|
|
|
1 |
2 |
2 |
2y1 + y2 + 4y3 ≥ 4 |
|
T |
= |
|
|
|
|
A |
|
2 1 |
3 |
||||
2y1 + y2 |
+ 3y3 ≥ 2 |
|
|
|
|
4 |
|
|
|
|
1 |
5 |
|||
yi ≥ 0, i 1:3

115
3 f = x1 − x2 + x3 + 2x4 − x5 → max
2x1 + 12x2 − x3 + 10x4 + 7x5 = 49 x1 + x2 + 6x3 + 2x4 + x5 = 14 xi ≥ 0 , i 1:5
ЗЛП в стандартной форме. В двойственной задаче на min (2 переменные без ограничений неотрицательности) все ограничения (их пять) имеют вид неравенств ≥
g = 49y1 + 14y2 |
→ min |
|
2y1 + y2 |
≥ 1 |
|
12y1 + y2 ≥ −1 |
||
− y1 |
+ 6y2 |
≥1 |
10y1 |
+ 2y2 |
≥ 2 |
|
7y1 + y2 ≥ −1 |
|
4 |
f = 2x1 + 7x2 |
− 3x3 + x4 − 2x5 → min |
|
x1 + 2x2 + x3 + 2x4 + x5 ≥ 10 |
|
|
3x1 − x2 + 2x3 − x4 + 4x5 ≤ 24 |
|
|
x1 + 2x2 + 3x3 + 4x4 + 5x5 ≤ 48 |
|
|
x1 + x2 + x3 + x4 + x5 = 12 |
|
|
x1 ≤ 0 |
x3 ≥ 0 , |
Прежде чем строить двойственную задачу необходимо в нежестких ограничениях сделать знаки неравенства одного типа. Умножим для этого 1-ое ограничение на (-1)и заменим min на max, поменяв знаки в целевой функции
f |
' = −2x |
− 7x |
2 |
+ 3x |
3 |
− x |
4 |
+ 2x |
5 |
→ max |
|
1 |
|
|
|
|
|
||||
|
− x1 − 2x2 − x3 − 2x4 |
− x5 ≤ −10 |
||||||||
|
3x1 − x2 + 2x3 − x4 + 4x5 ≤ 24 |
|||||||||
|
x1 + 2x2 + 3x3 + 4x4 + 5x5 ≤ 48 |
|||||||||
|
x1 + x2 + x3 + x4 + x5 = 12 |
|||||||||
|
|
x1 ≤ 0 |
|
|
x3 ≥ 0 , |
|
|
|||
Ограничение x1 ≤ 0 можно преобразовать либо в ограничение неотрицательности путем замены x1' = −x1 ≥ 0, либо включив данное неравенство в систему ограничений. Выберем, например, первый способ. Тогда получим

116
f ' = 2x1' − 7x2 + 3x3 − x4 + 2x5 → max x1' − 2x2 − x3 − 2x4 − x5 ≤ −10
−3x1' − x2 + 2x3 − x4 + 4x5 ≤ 24
−x1' + 2x2 + 3x3 + 4x4 + 5x5 ≤ 48
− x1' + x2 + x3 + x4 + x5 =12
x' |
≥ 0 |
x |
3 |
≥ 0 , |
1 |
|
|
|
К полученной ЗЛП запишем двойственную.
g = 10y1 + 24y2 + 48y3 +12y4 → min
y1 − 3y2 − y3 − y4 ≥ 2
|
− 2y1 − y2 + 2y3 + y4 = −7 |
|
|
− 3y1 + 2y2 + 3y3 + y4 ≥ 3 |
|
|
− 2y1 − y2 |
+ 4y3 + y4 = −1 |
|
− y1 + 4y2 |
+ 5y3 + y4 = 2 |
|
yi ≥ 0, i 1:3 |
|
5 |
f = x1 + 3x2 + 5x3 → min |
|
|
− 2x1 + x2 − 4x3 ≤ −2 |
|
|
x1 + 4x2 + 5x3 ≥12 |
|
x1 + x2 + x3 = 10 x2 ≥ 0
Сменим знак на обратный в 1-ом неравенстве (умножив его на (-1)) и, применив схему в обратную сторону, построим двойственную задачу.
f = x + |
3x |
2 |
+ 5x |
3 |
→ min |
g = 2y1 +12y2 +10y3 → max |
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
2x |
1 |
− x |
2 |
|
+ 4x |
3 |
≥ 2 |
2y1 + y2 + y3 = 1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
x + 4x |
2 |
|
+ 5x |
3 |
≥12 |
− y1 + 4y2 + y3 ≤ 3 |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
x + x |
2 |
+ x |
3 |
= 10 |
4y1 + 5y2 + y3 = 5 |
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
y1 ≥ 0 , y2 ≥ 0 |
||
|
|
x |
2 |
|
≥ 0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С помощью двойственной ЗЛП можно решить вопрос о разрешимости или неразрешимости исходной задачи, оценить значение ее целевой функции и, наконец, найти решение исходной задачи, зная решение двойственной, которую, зачастую, легче решить, чем исходную.

117
hТак, в примере 1 двойственная задача содержит всего две переменные и ее можно решить, например, графическим способом, тогда как исходная имеет четыре переменные. Более того, если внимательно посмотреть на систему ограничений двойственной задачи в
примере 1, то можно убедиться, что она имеет всего одно допустимое решение, которое и будет оптимальным. Это следует из того, что система
2y1 + y2 = 7
4y1 − y2 = −1
имеет единственное решение ( y1 = 1, y2 = 5 ) которое удовлетворяет остальным ограничениям. Итак, оптимальным решением двойственной задачи будет вектор Y = (1 , 5) . При этом gmin = 44. Применение теорем двойственности и соотношений дополняющей нежесткости (о них см. ниже) позволяет сразу выписать решение исходной задачи:
x |
|
= 0, x |
|
= 0, |
2x + 4x |
|
|
= 9 |
x |
|
= |
5 |
|
f |
|
= 7 |
37 |
+ |
5 |
= 44 |
h |
|
|
|
|
|
|
6 |
|
|
6 |
6 |
|||||||||||||
|
2 |
|
4 |
|
1 |
3 |
|
|
3 |
|
|
|
max |
|
|
|
|
|||||
|
|
|
|
|
x − x |
|
= 7 |
x |
= |
37 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
6 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим теперь более подробно свойства пары двойственных задач. Ниже исходную и двойственную задачи будем называть задачами (I) и (II) соответственно.
Лемма 1.
Если X[N] и Y[M ] - произвольные допустимые решения задач (I) и (II) соответственно, то f (X ) ≤ g(Y)
Доказательство. |
|
f (X ) = C[N] X[N] = C[N1 ] X[N1 ]+ C[N2 ] X[N2 ] |
( * ) |
Из системы ограничений задачи (II) |
|
C[N1 ] ≤ Y[M ] A[M, N1 ] |
|
C[N2 ] ≤ Y[M ] A[M, N2 ] |
|
Подставляя последние выражения в (*) имеем |
|
f(X ) ≤ Y[M ] A[M , N1 ] X[N1 ]+ Y[M ] A[M, N2 ] X[N2 ] =
=Y[M ] A[M, N] X[N] ≤ Y[M ] b[M ] = g(Y)
■
Лемма 2
Пусть X*[N] - допустимое решение ЗЛП (I): ε[N] ≥ 0[N]
Y *[M ] - допустимое решение ЗЛП (II): g(Y * ) = f (X * )
Доказательство.
Запишем (I) в стандартной форме
f (X |
* |
' |
] |
' |
] |
= |
' |
' |
~ |
' |
' |
~ |
|
|
) = C[N |
X[N |
( т.к. ε[N |
] = 0[N |
] ) = Y[M ] A[M , N |
] X[N |
] = Y[M ] b[M ] |
||||||
Возьмем в качестве |
Y |
* |
[M ] =ˆ |
~ |
|
|
|
|
|
|
|||
|
Y[M ]. Тогда |
|
|
|
|
||||||||
g(Y * ) = f (X * )

118
При этом согласно лемме 1, Y *[M ]- оптимальное решение ЗЛП (II), т.к. для любого допустимого решения Y [M] ЗЛП (II)
|
g(Y) ≥ f (X * ) = g(Y * ) |
X *[N]- оптимальное решение ЗЛП (I) в силу того, что по лемме 1 |
|
f (X * ) = g(Y * ) ≥ f (X ) для любого X[N] - допустимого решения ЗЛП (II) ■ |
|
Теорема 1. |
|
ЗЛП (I) разрешима |
ЗЛП (II) разрешима |
При этом g(Y * ) = f (X * ) для X *[N] и Y *[M ] - оптимальных решений ЗЛП (I) и (II) соответственно.
Доказательство.
Доказательство второй части теоремы проведено в лемме 2. Докажем необходимость и достаточность в первой части условия теоремы
Для разрешимости ЗЛП необходимо и достаточно: 1) -ия хотя бы одного допустимого решения: б) ограниченности целевой функции на множестве решений.
Если ЗЛП (I) разрешима X *[N]- ее оптимальное решение. Тогда (а) по лемме 2
Y *[M ]- допустимое решение ЗЛП (II), а по лемме 1 (б) g(Y * ) = f (X ) X[N]- допустимого решения ЗЛП (I) ЗЛП (II) разрешима.
Доказывается аналогично, считая исходной задачей ЗЛП (II). ■
hПервая теорема двойственности устанавливает тот факт, что обе задачи (I) и (II) разрешимы или неразрешимы одновременно и значения целевых функций обеих задач на оптимальных решениях совпадают. Таким образом, чтобы установить разрешимость задачи и найти оптимальное значение целевой функции достаточно решить ту ЗЛП из пары
двойственных задач, которая решается легче. Так, в примере на основании решения
двойственной задачи (см. предыдущее замечание) из 1-ой теоремы двойственности следует, что исходная задача (I) разрешима и максимальное значение ее целевой функции
|
|
|
|
|
|
fmax = gmin = 44 |
|
h |
||
Рассмотрим еще один пример |
|
|
|
g = 12y1 → min |
||||||
|
|
|
|
|
|
|
|
|
||
( I ) |
f = x1 + x2 + 3x3 + 2x4 |
→ max |
|
|
( II ) |
2y ≥ 1 |
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2x1 + 3x2 + 4x3 + x4 =12 |
|
|
|
3y1 ≥ 1 |
|||||
|
x |
i |
≥ 0 , i 1: 4 |
|
|
|
|
4y1 ≥ 3 |
||
|
|
|
|
|
|
|
|
y1 ≥ 2 |
||
|
|
|
|
|
|
|
|
|
||
Множеством допустимых решений задачи (II) является |
D = {y1 : y1 ≥ 2} |
|||||||||
|
|
|
|
|
1 |
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1/3 |
3 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|

 D и E одновременно не пусты.
D и E одновременно не пусты. Пусть
Пусть