Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сыктывкарский Государственный Университет им. Питирима Сорокина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Зад лин прогр и мет их решения 16 12 08

.pdf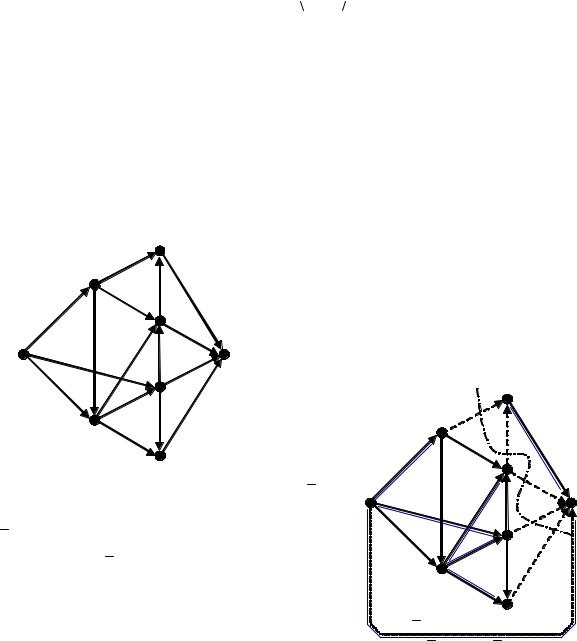

Скачиваний:

Добавлен:

29.03.2016

Размер:

7.61 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2822 23 24 25 26 27 28 > Следующая >>>

210 Длина критического пути равна 28. Дуги критического пути выбираются из условия

vj(u) −v i(u) = t[u]

(выделены на рисунке жирными линиями).

1. Вышеописанный алгоритм применяется и для поиска кратчайшего пути в сетевой модели задачи об аренде. Там "правильная"нумерация уже заложена в постановке задачи.

2. С задачей о дереве кратчайших путей тесно связана задача о кратчайшем дереве

– связывающем дереве с минимальной суммой длин дуг. Она решается при помощи

алгоритма Прима-Краскала, который основан на выделении связывающего дерева с "правильной" нумерацией [9]

3. Максимальный поток в сети

Эта задача является частным случаем СТЗ с ограничением пропускных способностей дуг. Пусть задан связный ориентированный граф M, N , положительный вектор пропускных

способностей его дуг d [N] и две выделенные вершины: i− – "источник" и i+	– "сток".
Требуется найти поток x[N], удовлетворяющий во всех вершинах кроме i− и i+	условию
баланса
a[i, N] x[N]= 0, i M \{i− ,i+},

и при этом поток, выходящий из "источника" i− (равный потоку, входящему в "сток" i+ )

				V = 1		N	− x	N	− .
							i−		i−
Эта сумма называется величиной потока.
Пример.
						Числа около дуг – их пропускные способности,
		3(1)				в	круглых скобках – дуговые потоки. На
		2	1	6(1)		остальных дугах потоки равны нулю.
		2	1	6(1)		Величина потока v = 3
6(1)						Величина потока v = 3
6(1)
		3		3
		3
i-	7(1)	5	4		i+
6(1)				6(1)
6(1)
		7	1	4(1)							3(3)
		5(1)									2(2)	1(1)	6(4)
										6(5)
Сведем задачу к СТЗ. Добавим к графу дугу u											3		3(3)
Сведем задачу к СТЗ. Добавим к графу дугу u									i-		3		i+
из i− в i+ .										7(6)	5(2)	4
										7(6)		4

c[u]=1,	c[N]= 0[N],									6(6)		6(6)
c[u]=1,	c[N]= 0[N],									6(6)
b[i+ ]= −b[i− ]= d [u]=1+V,											7(1)	1(1)	4(4)
b[i+ ]= −b[i− ]= d [u]=1+V,													4(4)

b[M0 ]= 0[M0 ],		M0 = M \{i+ ,i−}.									5(3)
Минимизация стоимости			потоков в		этой сети					u
означает	минимизацию			перевозки	по		дуге			u	[u]=1 x[u]=1
означает	минимизацию			перевозки	по		дуге
										c

211

u (x[u]=1), т.е. максимизацию потока V через исходную сеть.

Запись полученной СТЗ в виде задачи линейного программирования выглядит следующим образом:

f = 0[N] x[N]+1 x[u]→ min

a[i− , N] x[N]− x[							]= −1−V
a[i− , N] x[N]− x[					u		]= −1−V
a[M0 , N] x[N]− 0[M0 ]= 0[M0 ]
a[i		, N] x[N]+ x[					]=1+V
a[i		, N] x[N]+ x[				u	]=1+V
	+
		− x[N]					≥ -d [N]
		− x[N]					≥ -d [N]
		− x[		]			≥ -1−V
		− x[	u	]			≥ -1−V
		x[N]≥ 0[N], x[u]≥ 0
		x[N]≥ 0[N], x[u]≥ 0

[ − ]

[

]

[ + ]

[

]

[

]

Выпишем двойственную

задачу ( g = v

, ρ

– вектор

двойственных переменных)

(1+V ) (v[i+ ]− v[i− ]− ρ [

])− ρ [N] d [N]→ max

v[ j(u)

]− v[i(u)]− ρ [u]≤ 0

v[i ]− v[i ]− ρ [

]≤1

−

ρ [N]≥ 0[N], ρ [u]≥ 0

Пусть теперь V – максимальная величина потока, идущего через сеть. Тогда x[u]=1 и

дуга u является дугой оптимального базисного дерева (на рисунке эти дуги выделены). Базисное дерево имеет такую структуру, что при удалении дуги u оно распадается на две компоненты связности (два поддерева, одно из которых содержит источник i− , а другое –

сток i+ ). Обозначим множества вершин этих поддеревьев через M− и M+ соответственно. Тогда дуги, идущие из M− в M+ и обратно из M+ в M− называются дугами разреза (прямыми (N+ ) и обратными (N− )), разделяющего источник и сток (при их удалении

"разрезаются " все пути из источника в сток). Пропускной способностью разреза называется сумма пропускных способностей прямых дуг разреза

C (M− ,M+ ) = 1		+		+
C (M− ,M+ ) = 1	N		d N	.

Ясно, что величина потока, складывающаяся из величин потоков на путях, идущих из источника в сток, должна быть не больше пропускной способности разреза (иначе поток "не пройдет" через разрез). Отметим, что потенциалы всех вершин из M− равны нулю

(т.к. v[i− ]= 0 и C[N]= 0[N]), а потенциалы всех вершин из M+ равны единице (т.к.

v[i+ ]= v[i− ]+ c[

]= 0+1=1 и

C[N]= 0[N]). Отсюда следует, что для всех дуг u N с

ненулевым потоком (кроме дуг разреза

N+

и N− )

ρ [u]= 0 . Далее, из соотношений

дополняющей нежесткости получаем

] (v[i+ ]− v[i− ]− ρ [

]−1)= 0

(

[

]

)

[

]

1/ − 0 − ρ

−1

= 0 ρ

= 0

212

По теореме двойственности для оптимальных решений прямой и двойственной задач находим

g = (1+V ) (v[i+ ]− v[i− ]− ρ [

])− ρ [N] d [N] = f = x[

] =1

1+V − ρ [N] d [N]=1 V = ρ [N] d [N]

Далее имеем

−

≥

V = ρ [N] d [N]≥ ρ N

d N

+ ρ N

d N

≥

ρ N

d N

≥ 1

= C (M− ,M+ )

Отсюда

следует,

что

при

V == C (M− ,M+ )

прямые дуги разреза должны быть

насыщенными ( x N+

= d N+ ), а на обратных дуговые потоки должны быть нулевыми

( x N

−

= 0 N

− ).

Алгоритм для нахождения максимального потока является вариантом метода потенциалов, однако, реально вводить b[M ],c[N] и дугу u нет необходимости. Основу алгоритма составляет систематический поиск путей из i− в i+ , поток по которым можно

увеличить. Найденный путь вместе с дугой u образует единственный цикл в базисном дереве и после увеличения потока на нем, он разрывается по насыщенной дуге (или по обратной дуге с нулевым потоком). При отсутствии путей, увеличивающих поток будет получено оптимальное решение.

Задача о выборе минимального разреза является также основой алгоритма при

распределении ограниченных ресурсов в сетевом графике [9, стр.185]

К сетевым транспортным моделям сводятся многие задачи о покрытиях и паросочетаниях на графах. В частности, доказательство теоремы Дилворта (минимальное число путей, содержащих все вершины графа равно максимальному числу попарно несравнимых вершин) сводится к решению специальным образом построенной СТЗ. Задачи о паросочетаниях в простых (двудольных) графах могут быть сформулированы в виде потоковых задач на сетях. Методы решения задач линейного программирования применимы ко многим задачам с матрицами из нулей и единиц (задача о различных представителях, задача о наилучшем покрытии или разбиении, задача о порядке исключения переменных) [9].

213

Упражнения и задачи

1. Геометрическая интерпретация ЗЛП

1-11. Решить следующие ЗЛП графически или убедиться в их неразрешимости.

. 1.	f = x1 + x2	→ max
	{x1 + x2	≤1

x1 ≥ 0, x2 ≥ 0

2. f = x1 + 2x2 → max

x1 + x2 ≤1

x1 − x2 ≤1 x1 ≥ 0, x2 ≥ 0

4.f = x1 + x2 → max

x1		+ 2x2				≤1
2x				+ x		≤	1
		1			2
			− x2		≤1
x1			− x2		≤1
x			− 2x			≤	1
	1				2
2x				− x	2	≤1
		1			2

x1 ≥ 0, x2 ≥ 0

6.f = x1 + x2 → min

	0	≤ x1			≤ 1
		≤	x2		≤ 2
	0
	0	≤ x1	+ x2		≤ 3

−1		≤ x	− x	2	≤ 0
		1

8.f = x1 + 2x2 → max

3x1		− 2x2	≤ 6
	− x1 + 2x2		≤ 4

	3x1	+ 2x2	≤12

	x	≥ 0
	1

3. f = x1 + 2x2 → max

x1 − x2 ≤1

x1 − 2x2 ≤1 x1 ≥ 0, x2 ≥ 0

5.f = x1 − x2 → min

x1 + x2				≤ 1
x	− 2x				≤		1
1				2
		+ 3x2				≤ 2
2x1
3x		+ 2x				≤ 3
	1				2
x	+ x		2	≥ 1 2
1
x1		≥ 0, x2					≥ 0

7.f = x1 − x2 → max

1		≤ x1 + x2 ≤ 2
		≤ x1 − 2x2 ≤ 3
2
	1	≤ 2x1 − x2 ≤ 2

		x1 ≥ 0, x2 ≥ 0

9.f = 2x1 + x2 → max

− x1	+ x2	≤ 2
x1 + 2x2 ≤ 7
x1 + 2x2 ≤ 7
4x1 − 3x2			≤ 6
4x1 − 3x2			≤ 6
x	≥ 0, x	2	≥ 0
1		2

10.f = 7x1 + 5x2 → min

x	+ x			≥ 3
1			2
x1	+ 5x2 ≥ 5
2x		+ x		2	≥ 4
1				2

214

11.f = −x1 + 2x2 → min

2x1	− 3x2 ≥ 0
x1 − x2		≤ 3
x1 − x2		≤ 3
2x	− x	2	= 4
1		2

12-15. Используя метод исключения неизвестных и графический способ, найти решения следующих ЗЛП:

12. f = 8x1 − 2x2

− 3x3

→ max

13.

= x1

+ x3 − 7x4

+ x5 → max

− x

+ 3x

+ x

≤ 4

− x

− 2x

= −7

7x1

− 2x3 ≤ 16

x2 − x3 − 4x4 + 6x5 = 24

− x

= 2

+ x

− x

−

+ 7x

= 32

x1 ≥ 0, x2 ≥ 0, x3 ≥ 0

xj ≥ 0, j 1: 5

14.

= −x1 + x2

+ x4

+ 3x5

→ min

+ 2x

− x

− 5x

= −5

x1 + x

2 + x3 − 2x4 + 5x5 = −2

− 2x2 + x3 + 3x4 − 3x5 = 6

x1 ≥ 0, x2 ≥ 0, x3 ≥ 0

15.

f = x1 + x2 + 2x3

− 9x4

→ max

2x1 − x2 + x3 − 4x4 ≤ 6

+ 2x2

− x3 + 7x4 = 5

5x1 + x2

− 3x4 = 11

+ x

− 3x

= 7

≥ 0,

j 1: 4

2.Базисные решения. Метод полного перебора вершин.

16-23. Найти базисы решений систем, приведенных в условиях (в случае вырожденности решения найти все его базисы).

x − x		=1	3x + 2x			=1
16. 1	2		17.	1	2
x1 ≥ 0, x2 ≥ 0			x1	≥ 0, x2 ≥ 0
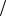
X0 = (1, 0)			X0	= (0 ,1/ 2)

215

− x2 = 0

+ x

= 2

= 0

18.

≥ 0, x2 ≥ 0

19. x1 − x2

≥ 0, x

≥ 0

= (0 , 0)

X0 = (1,1)

x + x

+ x

x + x

+ x

= 0

20. x1

− x3

= 0

21. x1

− x2

+ x3

= 0

≥ 0, i 1:3

= (1/ 2, 0 ,1/ 2)

X 0

= (0 , 0 , 0)

+ x2 + x3 + x4 =1

+ x

= 0

− x2

+ x3

− x4 =1

x1 − x2 + x3 − x4 = 0

22. x1

23.

+ x2 − x3 + x4 = 0

≥ 0, i 1: 4

= (1, 0 , 0 , 0)

X 0

= (0 , 0 , 0 , 0)

24-27. Найти решения следующих ЗЛП методом полного перебора вершин.

24.

f = x1 + x2

+ x3

→ max

25.

f = x1 + x2

+ 2x3

+ 3x4

→ min

− x

+ x

≤ 4

2x − x

+ x

−

≤ 6

2x1 + x2 + x3 ≤ 3

+ x2 + 3x3 + 4x4 =12

+ x

+ 2x

≤ 6

− x

+ x

− x

= 2

+ 2x2 − x3 ≤ −3

xj ≥ 0, j 1:4

− x1

26.

f = x1

+ 2x2 − 3x3

→ max

27.

= x1 + x2

− 4x3 + 2x4

→ max

− x +

−

+ x

= −4

− x1 + 2x2 + 2x3 ≤1

3 x1 − x2 − x3 + 2x4 ≤ −3

x1 + x2 − x3 = 0

x + 5x

+ x

+ 3x

≤ 4

x1 ≥ 0, x2 ≥ 0, x3 ≥ 0

≥ 0,

≥ 0

216

3. Прямой алгоритм симплекс-метода.

28-45. Решить ЗЛП, рассматривая в качестве начального базисного решения приведенное в условии.

28.

f = x1 − 2x2

+ x3 → max

29.

f = x1 + x2 + x3 → max

x + 4x

+ x

= 5

− x + x

+ x

= 2

x1 − 2x2 − x3 = −1

3x1 − x2 + x3 = 0

x1 ≥ 0, x2 ≥ 0, x3 ≥ 0

= (1,1, 0)

= (0 ,1,1)

30.

f = 2x1 + x2

+ 3x3 + x4

→ max 31.

f = 6x1 + x2

+ 4x3

− 5x4 → max

x + 2x

+ 5x

− x

= 4

3x + x

− x

+ x

x1 − x2 − x3 + 2x4 =1

5x1 + x2 + x3 − x4 = 4

xj ≥ 0, j 1:4

= (0 , 0 ,1,1)

X0 = (1, 0 , 0 ,1)

32.

f = x1 + 2x2

+ 3x3 − x4

→ max

33.

f = x1 − 3x2

− 5x3

− x4

→ max

x − 3x

− x

− 2x

= −4

x + 4x

+ 4x

+ x

= 5

x1 − x2 + x3

= 0

x1 + 7x2 + 8x3 + 2x4 = 9

xj ≥ 0, j 1:4

= (0 ,1,1, 0)

X0 = (1, 0 ,1, 0)

34.

f = x1 + x2 + x3

+ x4 → max

35.

f = x1 + 2x2 − x3

+ x4 → max

x + 3x

+ x

+ 2x

= 5

x + x

− 2x

+ 3x

2x1

− x3 + x4 =1

2x1 − x2 − x3 + 3x4 = 2

xj ≥ 0, j 1:4

= (0 ,1, 0 ,1)

= (0 , 0 ,1,1)

36.

f = x1 + x2 + x3

+ x4

+ x5 → max

2x + 3x

+ 5x

+ 7x

+ 9x

=19

− x2

+ x4 + 2x5 = 2

≥ 0,

j 1:5

= (0 , 0 ,1, 2 , 0)

217

37.

f = −2x1 + x2 + x3 − x4

+ 4x5

+ x6 → max

3x + x

+ 2x

+ 6x

+ 9x

+ 3x

=15

x1 + 2x2 − x3

+ 2x4 + 3x5 + x6 = 5

xj ≥ 0,

j 1:6

= (1, 0 , 0 , 0 , 0 ,4)

38.

f = x1 + x2 + 2x3

− x4 + x5 − x6 → max

x + 3x

+ x

− 3x

+ 4x

+ x

= 6

x1 − x2 − x3

+ x4

− x6 = 2

xj ≥ 0,

j 1:6

= (0 , 0 , 0 , 0 ,1,2)

39.

f = x1 − x2

+ x3

+ x4 − x5 − x6 → max

+ x

+ 3x

= 7

− x3

+ x5 − x6 = −2

+ x3

+ x4 + x5 + 2x6 = 5

≥ 0,

j 1:6

X0 = (0 , 0 , 2 , 0 ,1,1)

40. f = 5x1 + x2 + 2x3 + x4 → max

41.

f = x1 + 3x2 + x3

− x4

→ max

− x

+ x

= 1

+ 2x

+ x

= 3

2x1 + x2

+ x4 = 5

− x1 + x2 + x3

xj ≥ 0, j 1: 4

xj ≥ 0, j 1:4

X0 = (0 , 0 ,1, 5)

= (0 , 0 ,1, 3)

42.

f = 3x1

+ 7x2 + 4x3 − 3x4 + 2x5

+ 2x6 → max

− x1 + 3x

2 + 2x3 + x4 + x5 + 3x6 = 3

4x1

− 2x2 − 3x3 − 4x4 + x5 − 7x6 = −2

xj ≥ 0,

j 1:6

= (0 , 0 ,1, 0 ,1, 0)

218

43.

f = x1 + 3x2

+ 2x3 + 4x4

− 2x5 → min

− x1

+ x3 − 2x4

= −2

x2 − x3 + x4 − 2x5 = 0

+ 5x

+ x

= 7

xj ≥ 0,

j 1:5

= (3,1,1, 0 , 0)

44.

f = 3x1

− 2x2 + x3 + 3x4 + 3x5

→ max

2x1 − x2 + x3 + x4 + x5 = 2

− 4x1 + 3 x2 − x3 − x4 − 3x5 = −4

+ 2 x

+ 3x

+ 5x

= 3

≥ 0,

j 1:5

= (1, 0 , 0 , 0 , 0)

45.

f = x1 + 3x2 − 2x3 − x4

+ x5 + 3x6 → max

x2 + x3 + x4 − x5 + x6 =1

− x2

− x3 + x4 + 4x5 − 3x6 = −1

+ x2

+ x4 + x5

+ x

≥ 0,

j 1:6

= (0 ,1, 0 , 0 , 0 , 0)

46-48. Решить следующие ЗЛП, предварительно преобразовав их к канонической форме.

46. f = −x1 + x2

− 2x3 + 3x4 + x5 → max

+ 2x

− x

− 2x

+ x

≤ 3

− x1

− x2 + x3 + 2x4 + x5

≤1

+ x

− x

≤1

≥ 0,

j 1:5

47.f = x1 + 2x2 − 4x3

	x	− x		− x			+
	1		2			3
	2x1 − x2				+ x3
− x		+ 3x		2	− 2x			3
	1			2				3
	xj	≥ 0,			j 1:

→ max

x4 ≤1

≤3

−x4 ≤ 2

4. Искусственные переменные.

219
48. f = x1 + x2				+ x3 − 2x4				→ min
2x1 − x			2			+ x4 ≤ 3
					+ x3 − x4 ≤1
x1 + x			2		+ x3 − x4 ≤1
	x1 + 2x2				− x3			≤1
	x1 + 2x2				− x3			≤1
	x	+ 3x		2	− 2x	3	+ x	4	≤1
	1			2		3		4
	xj	≥ 0,			j 1:4

49-58. Решить ЗЛП, используя метод искусственных переменных.

49.

f = x1 + 4x2

+ x3 → max

50.

f = x1 −10x2

+ x3 → max

x − x

+ x

= 3

− x + 5x

+ 7x

=13

2x1 − 5x2

− x3 = 0

x1 +14,5x2 + 7x3 =15

x1 ≥ 0, x2 ≥ 0, x3 ≥ 0

51.

f = x1

+ 2x2

+ 3x3

− 4x4 → max

52.

f = x1 − 4x2 + 3x3

+ 10x4 → max

+ x

− x

+ x

= 2

x + x

− x

+ x

= 0

x1 +14x2 +10x3 −10x4 = 24

x1 +14x2 +10x3 −10x4 =11

xj ≥ 0, j 1:4

53.

f = x1

− 5x2

− x3 + x4 → max

54.

f = x1 + 10x2

− x3

+ 5x4

→ max

+ 2x

− x

+ 3x2 + 3x3 + x4 = 3

2x1

+ 3x3 − x4 = 4

− x1 + 2x2 + 3x3 + x4 = 2

+ 5x

+ x

− x

= 5

xj ≥ 0,

j 1:4

≥ 0,

j 1:4

55.f = −2x1 + 2x2 + x3 + 2x4 − 3x5 → max

− 2 x1 + x				2 − x3 − x4		=1
		− x2		+ 2x3 + x4 + x5 = 4
x1		− x2		+ 2x3 + x4 + x5 = 4
	− x	+ x	2	− x	5	= 4
	1		2		5
	xj ≥ 0,			j 1:5

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2822 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016327.17 Кб77Думин И.В. Другая Русь.doc
#
29.03.2016114.03 Кб212Е.А. Шевченко УМКРУНТ фольклор русский.docx
#
28.03.2016159.74 Кб82Евгений Онегин статья Маймина.doc
#
28.03.2016748.03 Кб16Еколе русс.doc
#
26.09.2019454.66 Кб35Загайнов Рудольф Максимович Психологическое мас...doc
#
29.03.20167.61 Mб29Зад лин прогр и мет их решения 16 12 08.pdf
#
29.03.2016470.27 Кб20Задания для самостоятельной работы.pdf
#
28.03.201646.84 Кб26Задания о выпуске продукции при ограниченных ресурсах.docx
#
28.03.2016152.06 Кб16Задачи к экзамену.doc
#
29.03.20167.64 Mб155Задачи ЛП и методы их решения .pdf
#
23.11.2018455.17 Кб9ЗАДАЧИ СОКОЛОВ!!!.doc