
Зад лин прогр и мет их решения 16 12 08
.pdf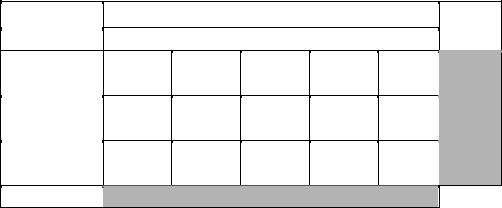
60
|
Новый план грузоперевозок |
|
|
|||
|
|
Потребитель |
|
|
|
|
Поставщик |
В1 |
В2 |
В3 |
В4 |
В5 |
Запасы |
|
|
|||||
A1 |
22 |
14 |
16 |
28 |
0 |
350 |
|
140 |
200 |
|
10 |
||
|
|
|
|
|||
A2 |
19 |
17 |
26 |
36 |
0 |
200 |
170 |
|
|
30 |
|
||
|
|
|
|
|
||
A3 |
37 |
30 |
31 |
39 |
0 |
300 |
|
|
|
165 |
135 |
||
|
|
|
|
|
||
Потребность |
170 |
140 |
200 |
195 |
145 |
|
Стоимость перевозок при этом = 15905.
Значение стоимости перевозок изменилось на 390 единиц, по сравнению с предыдущей стоимостью.
3 этап.
Полагая потенциал U1 = 0, определяем остальные потенциалы из соотношения
U j + Vi = Ci, j (i = 1..m, j = 1..n),
просматривая все занятые клетки. Потенциалы:
U1 |
= 0, |
|
|
V2 |
= C1,2 |
− U1 |
= 14, |
V3 |
= C1,3 |
− U1 |
= 16, |
V5 |
= C1,5 |
− U1 |
= 0, |
U3 |
= C5,3 |
− V5 |
= 0, |
V4 |
= C3,4 |
− U3 |
= 39, |
U 2 |
= C4,2 − V4 |
= −3, |
|
V1 |
= C2,1 |
− U 2 |
= 22. |
Определяем значения оценок, для всех свободных клеток:
Si, j = Ci, j − (V j − Ui ).

61
|
|
Значения оценок |
|
|
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
A1 |
0 |
|
|
-11 |
|
A2 |
|
6 |
13 |
|
3 |
A3 |
15 |
16 |
15 |
|
|
Выделенные оценки не являются оптимальными, а именно:
S1,4 = C1,4 − (V4 − U1 )= −11.
Выбираем оценку S1,4 = −11 .
Строим для этой клетки цикл, помечая клетки цикла знаками "плюс" и "минус".
План грузоперевозок
|
|
|
|
Потребитель |
|
|
|
|
|
Потенциалы |
|
|||
Поставщик |
|
|
|
|
|
|
|
|
|
|
|
Ui |
|
|
В1 |
|
В2 |
|
В3 |
В4 |
|
В5 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
A1 |
|
22 |
|
14 |
16 |
|
+ |
28 |
– |
0 |
|
0 |
|
|
|
|
140 |
|
200 |
|
|
|
10 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
A2 |
170 |
19 |
|
17 |
26 |
|
30 |
36 |
|
0 |
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A3 |
|
37 |
|
30 |
31 |
|
– |
39 |
+ |
0 |
|
0 |
|
|
|
|
|
|
|
|
165 |
|
135 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потенциалы |
22 |
14 |
16 |
39 |
0 |
|
Vj |
||||||
|
|
|
|
|
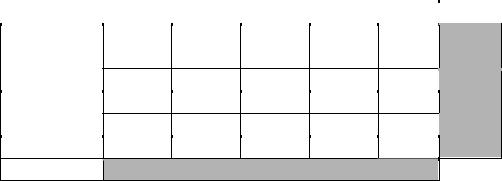
Перемещаем по циклу груз величиной в 10 единиц. В результате перемещения по циклу получим новый план.
62
Новый план грузоперевозок
|
|
|
Потребитель |
|
|
|
|
Поставщик |
|
|
|
|
|
|
Запасы |
В1 |
В2 |
В3 |
В4 |
В5 |
|
||
|
|||||||
|
|
|
A1 |
22 |
14 |
16 |
28 |
0 |
350 |
|
140 |
200 |
10 |
|
||
|
|
|
|
|||
A2 |
19 |
17 |
26 |
36 |
0 |
200 |
170 |
|
|
30 |
|
||
|
|
|
|
|
||
A3 |
37 |
30 |
31 |
39 |
0 |
300 |
|
|
|
155 |
145 |
||
|
|
|
|
|
||
Потребность |
170 |
140 |
200 |
195 |
145 |
|
Стоимость перевозок при этом = 15795.
Значение стоимости перевозок изменилось на 110 единиц, по сравнению с предыдущей стоимостью.
4 этап.
Полагая потенциал U1 = 0, определяем остальные потенциалы из соотношения
U j + Vi = Ci, j (i = 1..m, j = 1..n),
просматривая все занятые клетки. Потенциалы:
U1 = 0,
V2 = C1,2 − U1 = 14,
V3 = C1,3 − U1 = 16,
V4 = C1,4 − U1 = 28,
U2 = C4,2 − V4 = 8,
U3 = C4,3 − V4 = 11,
V1 = C2,1 − U 2 = 11,
V5 = C3,5 − U3 = −11.
Определяем значения оценок, для всех свободных клеток:
Si, j = Ci, j − (Vj − Ui ).
63
|
|
Значения оценок |
|
|
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
A1 |
11 |
|
|
|
11 |
A2 |
|
-5 |
2 |
|
3 |
A3 |
15 |
5 |
4 |
|
|
Выделенные оценки не являются оптимальными, а именно:
S2,2 = C2,2 − (V2 − U 2 )= −5.
Выбираем оценку S2,2 = −5 .
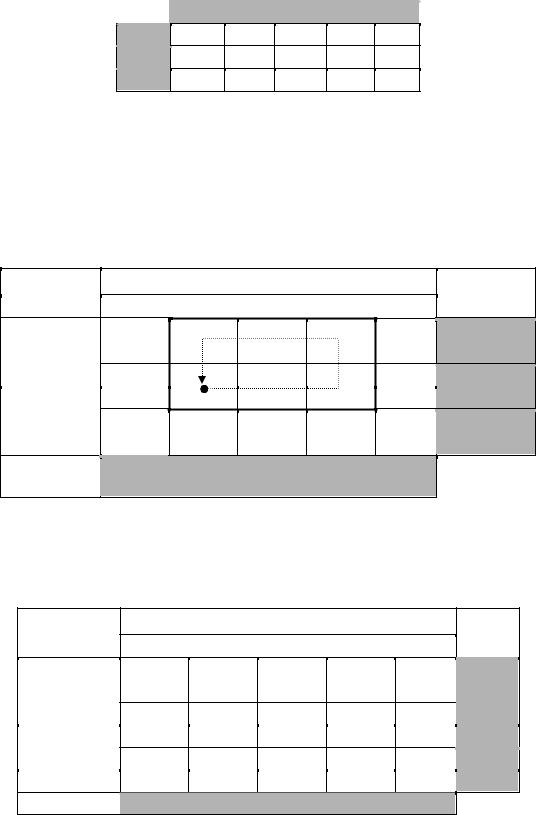
Строим для этой клетки цикл, помечая клетки цикла знаками "плюс" и "минус".
План грузоперевозок
|
|
|
Потребитель |
|
|
|
Потенциалы |
|
Поставщик |
В1 |
В2 |
|
В3 |
В4 |
|
В5 |
Ui |
|
|
|
|
|||||
A1 |
22 |
– |
14 |
16 |
+ |
28 |
0 |
0 |
|
140 |
|
200 |
10 |
|
|
||
|
|
|
|
|
|
|||
A2 |
19 |
+ |
17 |
26 |
– |
36 |
0 |
8 |
170 |
|
|
|
30 |
|
|
||
|
|
|
|
|
|
|
||
A3 |
37 |
|
30 |
31 |
|
39 |
0 |
11 |
|
|
|
|
155 |
|
145 |
||
|
|
|
|
|
|
|
||
Потенциалы |
11 |
14 |
|
16 |
28 |
|
-11 |
|
Vj |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Перемещаем по циклу груз величиной в 30 единиц. В результате перемещения по циклу получим новый план.
|
Новый план грузоперевозок |
|
|
|||
|
|
Потребитель |
|
|
|
|
Поставщик |
В1 |
В2 |
В3 |
В4 |
В5 |
Запасы |
|
|
|||||
A1 |
22 |
14 |
16 |
28 |
0 |
350 |
|
110 |
200 |
40 |
|
||
|
|
|
|
|||
A2 |
19 |
17 |
26 |
36 |
0 |
200 |
170 |
30 |
|
|
|
||
|
|
|
|
|
||
A3 |
37 |
30 |
31 |
39 |
0 |
300 |
|
|
|
155 |
145 |
||
|
|
|
|
|
||
Потребность |
170 |
140 |
200 |
195 |
145 |
|
Стоимость перевозок при этом = 15645.

64
Значение стоимости перевозок изменилось на 150 единиц, по сравнению с предыдущей
стоимостью.
5 этап.
Полагая потенциал U1 = 0, определяем остальные потенциалы из соотношения
U j + Vi = Ci, j (i = 1..m, j = 1..n),
просматривая все занятые клетки.
Потенциалы:
U1 |
= 0, |
|
|
V2 |
= C1,2 |
− U1 |
= 14, |
V3 |
= C1,3 |
− U1 |
= 16, |
V4 |
= C1,4 |
− U1 |
= 28, |
U2 = C2,2 − V2 = 3,
U3 = C4,3 − V3 = 11,
V1 = C2,1 − V2 = 16,
V5 = C3,5 − U3 = −11.
Определяем значения оценок, для всех свободных клеток:
|
Si, j = Ci, j − (Vj − Ui ). |
|
|
||
|
|
Значения оценок |
|
|
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
A1 |
6 |
|
|
|
11 |
A2 |
|
|
7 |
5 |
8 |
A3 |
10 |
5 |
4 |
|
|
Так как все оценки неотрицательны, то полученный план является оптимальным.
Транспортная задача решена.
65
|
Оптимальный план грузоперевозок |
|
|
|||
|
|
Потребитель |
|
|
|
|
Поставщик |
В1 |
|
В3 |
В4 |
В5 |
Запасы |
|
|
|
||||
A1 |
22 |
14 |
16 |
28 |
0 |
350 |
|
110 |
200 |
40 |
|
||
|
|
|
|
|||
A2 |
19 |
17 |
26 |
36 |
0 |
200 |
170 |
30 |
|
|
|
||
|
|
|
|
|
||
A3 |
37 |
30 |
31 |
39 |
0 |
300 |
|
|
|
155 |
145 |
||
|
|
|
|
|
||
Потребность |
170 |
140 |
200 |
195 |
145 |
|
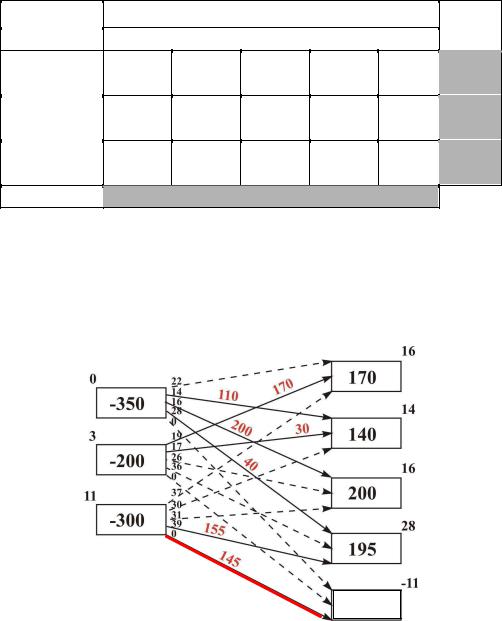
Стоимость перевозок при этом = 15645.
145 единиц груза из хранилища A3 осталось нераспределенным.
Графически оптимальный план грузоперевозок можно представить в виде графа со значения перевозок на дугах.
145

66
5. ЗАДАЧА ОБ АРЕНДЕ ОБОРУДОВАНИЯ
5.1. Предварительные сведения. Бесконтурные сети
Сети являются частным случаем графов. Ограничимся случаем бесконтурных сетей, используемых в задачах контрольных заданий.
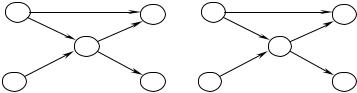
Граф является математическим, формальным представлением объектов, между которыми попарно установлены некоторые связи [9,18,19]. Объекты называются вершинами и графически изображаются кружками. Связи считаются установленными между некоторыми парами из различных вершин и считаются односторонними. Графически связь изображается линией со стрелкой, или дугой, соединяющей две вершины. Согласно направлению связи, т.е. направлению стрелки, соединяемые вершины являются началом и концом дуги, или, другими словами, начальной и конечной вершинами дуги.
Будем считать, что между двумя вершинами есть не более одной дуги (нет "параллельных" дуг). Формально этого можно добиться, разбив дугу на две с помощью промежуточной вершины. В дальнейшем дугу будем записать в виде упорядоченной пары (a, b), где a – начало дуги, b – конец дуги.
Путём из вершины v0 в вершину vk , или путём, начинающимся в v0 и заканчивающимся в vk , называется последовательность различных (возможен только случай v0 = vk ) вершин
(v0 ,v1,...,vk−1,vk ) , где пары (v0 ,v1) , (v1,v2 ) , …, (vk−1,vk ) различны и являются дугами. Графически путь представляет непрерывную направленную линию из дуг, согласованную с направлениями стрелок ("движения по стрелкам"). Если v0 = vk , т.е. если начало пути совпадает с концом пути, то путь называется контуром. Цепочкой из вершины v0 в вершину vk называется последовательность (v0 ,v1,...,vk−1,vk ) из различных вершин, в которой дугами являются (v0 ,v1) или (v1,v0 ) , (v1,v2 ) или (v2 ,v1) , и т.д. Таким образом, цепочка соответствует линии из v0 в vk без учёта направления стрелок. Замкнутая цепочка называется циклом.
Будем предполагать, что любые две вершины можно соединить цепочкой (соответствующий граф называется связным).
b |
|
d |
f |
( a, c, b, d, f ) – |
|
||||
|
|
|
|
|
a |
|
|
|
путь |
|
|
|
|
|
|
|
|
|
( b, d, f, c, b ) – |
|
|
|
c |
контур |
|
|
|
|
|
|
|
|
|
( a, b, c, f ) – |
Рис. 1 |
|
|
|
цепочка |
|
|
|
|
( a, b, c, a ) – цикл |
Определение. Конечная совокупность вершин и дуг (и их графическое изображение) называется сетью, если выполняются условия:
а) связности; б) отсутствия петель (начало и конец дуги различны);
в) отсутствие параллельных дуг. ♦
67
Определение. Сеть называется бесконтурной, или упорядоченной сетью, если в ней нет контуров. ♦
Замечание. В литературе встречается также термин ациклическая сеть.
Сеть на рис.1 не является бесконтурной, т.к. есть контур (b, d, f, c, b).
Н у м е р а ц и я вершин сети – это сопоставление вершинам номеров – натуральных чисел, при этом различным вершинам сопоставляются различные номера.
Определение. Нумерация называется правильной, если:
а) номера идут подряд: 1, 2, …, m, где m – число вершин;
б) номер начала дуги меньше номера конца дуги, т.е. все дуги записываются в виде (i, j) , где i < j . ♦
В сетях, имеющих контур, правильной нумерации не может быть, так как для вершины контура с номером N получаем противоречивое неравенство n < ... < n .
В бесконтурных сетях правильная нумерация возможна и может быть проставлена по следующей процедуре (алгоритм Форда).
1.Найдём вершину, которая не является началом никакой дуги, т.е. из которой дуги не выходят. Такая вершина легко может быть найдена, если, начиная с любой вершины, двигаться по стрелкам дуг, переходя из вершины в вершину.
2.Присвоим найденной вершине текущий номер. Первый раз таким номером является m – число вершин сети.
3.Уменьшим текущий номер на одну единицу. Вычеркнем или пометим как-либо дуги, заканчивающиеся в вершине, только что пронумерованной. В дальнейшем считаем, что этих дуг нет в сети. Возвращаемся к шагу 1, т.е. все повторяем с начала.
Замечание. 1. Если не удаётся найти вершину в шаге 1, то в сети есть контур и правильная нумерация невозможна, так что алгоритм Форда является также и проверкой, будет ли сеть бесконтурной.
2. Правильных нумераций в сети может быть несколько.
1 |
2 |
1 |
4 |
|
|
||
|
5 |
|
3 |
6 |
7 |
2 |
5 |
Неправильная нумерация |
|
Правильная нумерация |
|
(1 и 2, 4 и 5 можно поменять местами)
5.2. Планы аренды. Постановка задачи
Некоторая фирма (пункт проката) предоставляет в аренду ценное оборудование. Предположим, что другая фирма планирует иметь это оборудование в течение времени [T нач ,T кон ] и может брать в аренду (оформлять аренду) в определенные моменты
t ,t , ,t ,t , где t =T <t < <t <t =T . Таким образом, имеются N отрезков
1 2 … N N+1 1 нач 2 … N N+1 кон
времени [t ,t ],[t ,t ], ,[t ,t ], в начале которых можно брать оборудование в аренду
1 2 2 3 … N N +1

68
(в другой трактовке – покупать новое оборудование), пользоваться им в течение некоторого целого числа отрезков, а в конце какого-либо отрезка возвращать (в другой трактовке – списывать). Отрезками времени могут быть месяцы, дни, недели, часы и т.п., причем один отрезок может состоять, например, из двух недель, другой – из целого квартала, третий – из
четырех дней и так далее. В дальнейшем отрезки [ti ,ti +1 ] для определенности будем
называть месяцами , а момент ti начала отрезка (начала i-го месяца) будем обозначать
просто через I . Таким образом, в аренду оборудование можно брать в моменты I=1,2,…,N и возвращать в моменты J=2,3,…,N+1.
Планом аренды называется последовательность очередных моментов оформления аренды (и возврата оборудования). В наших обозначениях – это возрастающая последовательность натуральных чисел (1,i1 ,i2 ,…,ik ,N +1). Общее количество планов аренды на N месяцев
совпадает с числом всех подмножеств {2, 3, ,N} и равно 2N - 1 . Примеры планов аренды:
1.(1,2,3,…,7) - план аренды на 6 месяцев, состоящий в том, аренда оформляется 6 раз – каждый раз на 1 месяц;
2.(1, 3, 5, 7) - план аренды на 6 месяцев, состоящий в том, аренда оформляется 3 раза – каждый раз на 2 месяца;
3.(1, 3, 7) - план аренды на 6 месяцев, состоящий в том, аренда оформляется 2 раза – первый раз на 2=3-1 месяца (первый и второй), второй раз на 4 месяца (третий, четвертый, пятый и шестой);
4.(1, 15) план аренды на 14 месяцев, состоящий в том, аренда оформляется 1 раз – с начала
1-го месяца на весь срок – до конца 14 -го месяца.
Предположим теперь , что фирма, предлагающая оборудование в аренду, установила заранее значения арендной платы (стоимости аренды) на все возможные отрезки времени. Пусть Cij
– стоимости аренды от начала i-го месяца до начала j-го месяца в некоторых единицах (у.е.), где 1 ≤ I < J ≤ N+1. Тогда несложно видеть, что число C1i1 + Ci1i2 +…+ Cik N+1 является суммарной арендной платой за весь период [T нач ,T кон ], то есть стоимостью плана аренды.
Простейшая задача об аренде (замене) оборудования состоит в нахождении при заданной таблице стоимостей аренды самого дешевого (самых дешевых, если их несколько) плана аренды, то есть оптимального плана аренды.
Пример. Пусть при N=3 cтоимости аренды Cij заданы в таблице
Из 4 планов аренды
j |
2 |
3 |
4 |
1) |
(1,2,3,4), С=4+6+6=16; |
|
|
|
i |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
4 |
9 |
15 |
2) |
(1,2,4), С=4+10=14; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
(1,3,4), С=9+6=15; |
|
|
|
2 |
– |
6 |
10 |
|
|
|
||
|
|
|
|
|
|
|
|
|
3 |
– |
– |
6 |
4) |
(1,4), С=15 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
план (1,2,4), то есть план "взять в аренду на |
||||
|
|
|
|
1мес. + 2 мес." является оптимальным планом |
||||
|
|
|
|
со |
стоимостью |
Сmin |
=14 |
у.е. |
69
5.3. Сетевая модель задачи и ее решение
Изобразим моменты i=1,2,..,N+1 в виде вершин графа, а пары (i,j) в виде ориентированных дуг этого графа (основные понятия теории графов и терминология приведены в Приложении). Проставим на дугах (i,j) соответствующие стоимости аренды Cij и будем считать их длинами этих дуг. Тогда произвольный план (1,i1 ,i2 ,… ,ik , N + 1) можно
представить как путь из вершины 1 в вершину N+1, а стоимость плана – длиной этого пути. Наоборот, каждый путь указанного вида является планом аренды. Оптимальным планом аренды будет кратчайший путь из 1 в N+1. Таким образом, задача об аренде оборудования является частным случаем известной задачи о нахождении кратчайшего пути (маршрута) [2- 6].
Полученный граф (сеть) с заданными числами-стоимостями на дугах называется сетевой моделью задачи об аренде оборудования, а нахождение оптимального плана (оптимальных планов) аренды как кратчайшего пути на этой сети – решением на сетевой модели.
Найдём путь методом потенциалов [9,16,19] для бесконтурных сетей.
На 1-м этапе находим потенциалы — числа VI для каждой вершины i, означающие
кратчайшие расстояния от вершины i |
до конечной вершины N+1. Потенциалы найдем, |
начиная с последней и далее по убыванию номеров вершин по формуле |
|
VN = 0; Vi = min { V j + C i j } , i = N |
− 1, N − 2,..., 1, |
j |
|
минимум берётся по всем дугам (i, j ), выходящим из вершины i .
На втором этапе, начиная с вершины i =1, находятся и выделяются дуги (i, j ), на которых потенциал начала дуги Vi в точности равен сумме потенциала конца дуги Vj и стоимости дуги Cij. Выделенные таким образом дуги дают кратчайший путь (пути), то есть оптимальные планы аренды. Потенциал V1 начальной вершины будет равен длине кратчайшего пути, то есть стоимости оптимального плана аренды.
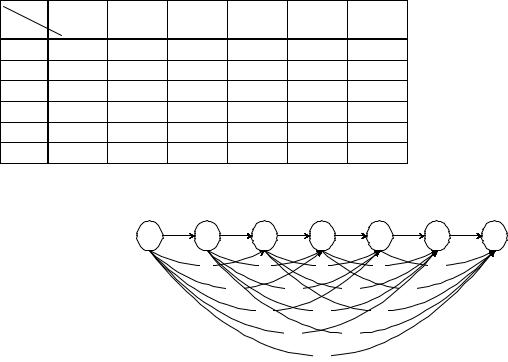
Пример 2. . Пусть при N=6 стоимости аренды Cij заданы в таблице:
J |
2 |
3 |
4 |
|
5 |
|
6 |
|
7 |
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
49 |
99 |
145 |
197 |
244 |
296 |
|
|
|
|
||||
2 |
– |
50 |
96 |
|
146 |
198 |
247 |
|
|
|
|
|||
3 |
– |
– |
48 |
|
95 |
|
147 |
189 |
|
|
|
|
||
4 |
– |
– |
– |
|
49 |
|
98 |
|
148 |
|
|
|
|
|
5 |
– |
– |
– |
|
– |
|
51 |
|
101 |
|
|
|
|
|
6 |
– |
– |
– |
|
– |
|
– |
|
53 |
|
|
|
|
|
Составим сетевую модель: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
49 |
2 |
50 |
3 |
48 |
4 |
49 |
5 |
51 |
6 |
53 |
7 |
|
|
|
|
99 |
|
96 |
|
95 |
|
98 |
|
101 |
|
|
|
|
|
|
|
145 |
|
146 |
|
147 |
|
148 |
|
|
|
|
|
|
|
|
|
197 |
|
198 |
|
189 |
|
|
|
|
|
|
|
|
|
|
|
244 |
|
247 |
|
|
|
|
|
|
|
|
|
|
|
|
|
296 |
|
|
|
|
|
|
