Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сыктывкарский Государственный Университет им. Питирима Сорокина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Зад лин прогр и мет их решения 16 12 08

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

7.61 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2821 22 23 24 25 26 27 28 > Следующая >>>

200

7.14.4. Метод потенциалов для решения

Найдем базисный план перевозок для

сетевой ТЗ

основного примера, приведенного выше

Базисный план в СТЗ определяется из

6 7

условий

-1

x[N \ N ']=0[N \ N ']

1 -1 -1

1 1

a[M, N '] x[N ']=b[M ]

-1

где

[M, N ']

связывающее дерево

(вспомним,

что

ранг

a[M, N ]

равен

-1

-7

-1

-3

N '

−1)

Решению

последней

системы

очень

помогает

правильная

нумерация

дуг

Обратным

ходом

метода

исключения

связывающего дерева, введенная выше.

Гаусса находим

Запишем двойственную ЗЛП к СТЗ

[

]

x 8 =5

v[M ] b[M ]→ max

x 7

[

]

v[M ] a[M, N ]≤C[N ]

x 6

С учетом структуры матрицы инциденций

[

]

x 5 =7

(в каждом

столбце ровно

2 ненулевых

[

]

элемента:

соответствует

концу

дуги

[

]

x 4

j(u)

и −1

соответствует

началу

дуги

x 3

=0+x 8 =5

[

]

[

]

i(u)) получим

x 2

=2+x

( ) ε[u]=v j(u) −v i(u) −C[u]≤0, u N

[

]

[

]

[ ]

x1 =0+x 2 +x

3−x 5−x

6 =5+6−7−3=1

[

]

[

]

[

]

[ ]

[

]

Нетрудно видеть, что левая часть

Начальный базисный план будет выглядеть

последнего неравенства есть оценка дуги и

так:

в текущем базисе N '.

-1

Таким

образом,

критерий оптимальности

задается условием ( ), а сами компоненты

вектора

двойственных

переменных

-3

(называемые

здесь

потенциальными)

определяются

из

условий равенства

нулю

оценок базисных дуг (дуг неравенства N ').

-7

( ) v j(u) −v i(u) =C[u], u N '

Система ( ) содержит уравнений на одно

Определим потенциалы вершин

меньше, чем переменных (

N '

−1), и

это позволяет при нахождении потенциалов

один

из

них

выбрать

произвольно.

Используя

правильную

нумерацию,

потенциалы удобно находить в порядке

возрастания номеров вершин (двигаясь по

ориентации

известному

потенциалу,

добавляем цену по дуге, двигаясь против

ориентации дуги - цену вычитаем).

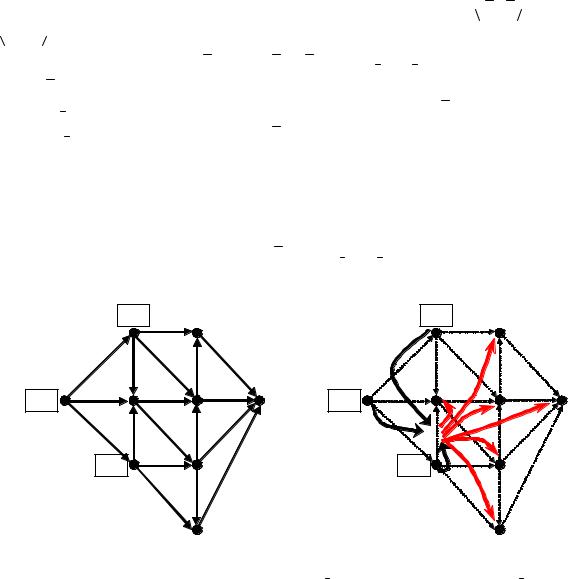
Теперь для каждой небазисной дуги (на рис.

выделены

пунктиром)

проверяем

выполнение неравенства

( ). Одна из дуг

u , для которой нарушается критерий оптимальности (штриховые линии на рис.)

201 вводится в базис. У нас имеется шесть таких дуг и шесть допустимых направлений улучшения решения (шесть основных циклов). Выберем какой-нибудь из них и зададим направление на нем в соответствии с ориентацией единственной небазисной дуги u основного цикла.

Выбирая λ по правилу

λ=min{x[u]u N'− -отрицательные дугицикла},

обеспечиваем ввод в базис дуги u , и выведение из него отрицательной дуги основного цикла (какой-либо), а дальше с перевозкой равной λ. Переход к новому решению заключается в изменении перевозок по циклу на величину λ: увеличение на положительных дугах и уменьшение на отрицательных дугах основного цикла.

v[0]=0

v[1]=v[0]+C[1]=0+1=1 v[2]=v[1]+C[2]=1+4 =5 v[3]=v[1]+C[3]=1+1= 2 v[4]=v[2]+C[4]=5+1=6 v[5]=v[1]−C[5]=1−1=0 v[6]=v[1]−C[6]=1−2 =−1 v[7]=v[2]+C[7]=5+1=6 v[8]=v[3]+C[8]= 2+1=3

	0	3	6
		3
1	1	1	2
1	1
-1	1		5
-1			6
1			1
1			1
		2	1
		2	2
	0	2	2
	0
		2
			3

1 4

− −	5
7

+ 5

u−

			λ = min{5,5,7}= 5
	-1		4
	1		4
	3	6	4	0
-3	3	6		0
-3	0		2	0
	0		2
	2
	-7	5	0

Это улучшенный базисный план f =5

На этом завершается одна итерация метода потенциалов. Закончим рассмотрение основного примера.

						202
		0		8				3
							0	3			6
											6	2-я итерация


						1		1				2
		1		1		1	1			1		2
		1		1			1			1
								1
7	2		4	1	6	2		4			1	6
7		1			6							6
		1		5
				5							5
						-1					5
						-1
		1					1	1	1
		1				1	1		1		1
						1					1
				4								2
												2
		2					0	2			1
							0				1
		2		1				2		1
				3				2
	(1)	u		(4)				(1)		(4)
	(3)			(0)		(3)					(0)
		(6)						(5)
	(2)						(2)
		(5)	(0)					(5)	(0)				= 4
												f	= 4
		0		8			0	3
								3			2
											2
												3-я итерация
			1			1		1				2
				1		1	1			1		2
				1			1	-3		1
								-3
7	2		4	1	6	2		4			1	2
7		2			6							2
		2		1
				1							1
						-5					1
						-5
		1					1	1	1
		1				1	1		1		1
						1					1
				5								2
												2
		3					-4	2			-3
							-4				-3
		2		1				2		1
				4				-2

u	(4)	(3)	(4)	(4)
(1)		(3)
(1)
(3)	(0)			(0)
(5)			(2)
(2)			(2)

(5)

(0)

(5)

(0)

f = 12

					203
	1		8			1	3
							3			3
										3
											4-я итерация
		1			1		1				2
1			1		1	1			1		2
1			1			1	-2		1
							-2
0		4	1	7	2		4			1	3
0	3			7							3
	3		2
			2							2
					0					2
					0
	1					1	1	1
	1				1	1		1		1
					1					1
			6								2
											2
	4					-3	2			-2
						-3				-2
	2		1				2		1
			5				-1
	(1)		(4)		(3)
					(3)		(4)		(4)
							(4)		(4)
(3)			(0)
	(5)									(0)
							(2)
(2)		u				(2)
						(2)			(0)
									(0)
	(5)	(0)
							(5)					= 0
											f	= 0
	1		8			1	3
							3			3
										3
											5-я итерация
		1			1		1				2
1			1		1	1			1		2
1			1			1	-2		1
							-2
0		4	1	7	2		4			1	3
0	3			7							3
	3		2
			2
					0					2
					0
	1		1			1	1	1
	1		1		1	1		1		1
					1					1
											2
	4		6			-3	2			1
			6			-3				1
	2						2		1
			5				-1
	(4)
(3)			(4)		(3)		(4)		(4)
			(4)				(4)		(4)
			(0)							(0)
	(2)
	u		(0)			(2)	(2)
(2)			(0)						(2)
(2)									(2)
	(5)						(5)				f	= 4
											f	= 4

					204
	1		8				1			3
										3			3
													3
														6-я итерация
		1					1			1				2
1			1				1		1			1		2
1			1						1	0		1
										0
0	4		1	7			2			4			1	3
0				7										3
			2
					0							2
					0
	1	1	1						1	1	1
	1		1				1		1		1		1
							1						1
														2
	5		3					-1		2		1
			3					-1				1
	2									2		1
			6							1
(3)	(4)		(4)				(3)			(4)		(4)
			(4)							(4)		(4)
			(0)
	(2)		u
	(2)	(2)	u						(2)	(2)		(2)		(0)
		(2)


	(5)									(5)
														f	= 0
	1		8				1			3
										3			3
													3
														7-я итерация
		1					1			1				2
1			1				1		1			1		2
1			1						1	0		1
										0
0	4			7			2			4			1	2
0				7										2
			2
					0							2
					0
	1	1	1	1					1	1	1
	1		1				1		1		1		1
							1						1
														2
	5		3					-1		2		1
			3					-1				1
	2									2		1
			6							1
					-1					4
										4
							1
				(3)		(4)		1	(4)
				1
Текущее решение			-3		0					2		0
оптимально							(2)			1
оптимально										(0)
					(2)	1		1
							1		(2)
							1		(2)
					-7
							2		0		Стоимость плана перевозок – 27 ед.
						(5)					(уменьшилась на 25 ед.)
										5

205

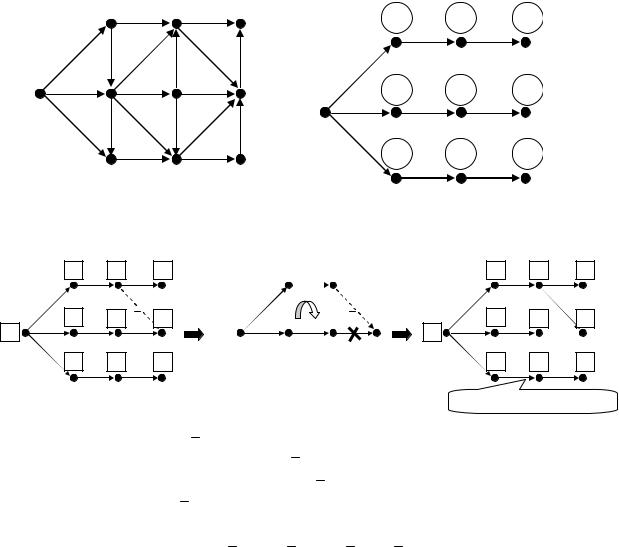
Опишем теперь построение начального допустимого базисного решения. Используем для этого метод искусственного базиса. Для этого построим расширение M, N графа

M, N :

M = M {i }, N = N Ni+ Ni−

Здесь: i - новая вершина

Ni+ - множество дуг, ведущих от пунктов производства к i

Ni− - множество дуг, идущих от i к остальным вершинам сети (потребления и промежуточным пунктам).

=0, C N

=0 N

−

= gz×1 N

−

(gz >C[N ] 1[N ]− достаточно большое число)

Вкачестве начального (искусственного) базиса можно принять

		N ' = N \ N = N+		N−
			i	i
-1					-1
	4						4
					0
						GZ
0	2	0			0 GZ		2	0
-3		0	-3					0
						GZ	GZ
				0		GZ
				0			GZ
							GZ
-7	0				-7		0
					0
						GZ
	5						5

"Искусственные" дуги образуют дерево типа "звезда". Дуговые потоки определяются очевидным образом: x[u]=−b i(u) , для u Ni+ , x[u]=b j(u) , для u Ni− . Ясно также, что данное базисное решение не является оптимальным (за счет цен, равных gz ).

206

7.14.5. Варианты СТЗ и родственные ей задачи

Следуя [9], перечислим несколько вариантов СТЗ и родственных ей экстремальных задач на графах, иллюстрирующих плодотворность идеи потенциалов.

а) СТЗ с ограничениями на пропускные способности дуг

c[N] x[N] → min

A[M, N] x[N] = b[M ]

0[N]≤ x[N]≤ d [M ]

d [N] – ограниченные пропускные способности дуг.

Двойственная задача с учетом d [N] выглядит следующим образом:

	v[M ] b[M ]− ρ [N] d [N] → max
	v[M ] A[M, N]− ρ [N] ≤ c[N]	,
	ρ [N]≥ 0[N]	,
	ρ [N]≥ 0[N]
	откуда критерий оптимальности запишется в виде
	v[ j(u)]− v[i(u)] ≤ c[u]+ ρ [u],
	где
	v[i(u)],v[ j(u)] – потенциалы начала и конца дуги u ,

ρ[u] – "рента на дуге " u .

1. Критерий оптимальности может быть записан и без участия рент.

2.Преобразованием сети, при котором каждая "ограниченная" дуга заменяется тремя "неограниченными" дугами (см. рис.)

			d[u]
			i+
	d[u]		c[u]
i	j	i	0	j
i	j	i	0	j
	c[u]
				0
				j-
				-d[u]

транспортная задача с ограничениями на пропускные способности дуг может быть сведена к СТЗ без ограничений пропускных способностей

б) Задача об оптимальном нормированном контурном потоке

c[N] x[N]→ min

A[M, N] x[N] = 0[M ] условие замкнутости потока

x[N]≥ 0[N]

l[N] x[N] =1 условие нормировки

207

Критерий оптимальности

v[ j(u)]− v[i(u)] ≤ c[u]− z l[u] v[M ] – потенциалы,

z – удельный убыток (убыток на единицу длины оптимального контура).

в) Двухкомпонентная задача

c[N] x[N] → min

A[M , N] x[N] = b[M ]

x[N]≥ 0[N]

В каждом столбце матрицы A[M, N] содержится по одному или по два ненулевых элемента.

Из задач, родственных транспортной рассмотрим следующие:

1.Дерево кратчайших путей

2.Задача о критическом пути

3.Максимальный поток по сети.

1.Дерево кратчайших путей

Зафиксируем вершину i0 в связном ориентированном графе M, N . Требуется найти кратчайшие пути из i0 во все остальные вершины (c[N] – длины дуг). Построим СТЗ с одним пунктом производства (вершина i0 ) имеющим отрицательную потребность

b[i0 ]=1− M

И потребителями (все остальные вершины графа) с единичным потреблением, т.е.

	1,				i ≠ i
b[i]					0
	=	−			i = i0	.
	=					.
	1		M	,


Ясно, что оптимальное решение этой задачи реализуется в виде дерева M, N ' , и это
будет дерево, в котором каждый путь из i0		в любую вершину j будет кратчайшим.

Иначе, предположив, что в оптимальном решении СТЗ путь от i0 до j не является кратчайшим и существует более короткий путь, удаляем примыкающую дугу к j из "старого" пути и получаем противоречие с оптимальностью решения СТЗ.

Вектор потенциалов при v[i0 ] = 0 в оптимальном решении СТЗ

[9, с. 161-163].

208

v[ j(u)] = v[i(u)]+ c[u], u N ' [ j(u)]≤ v[i(u)]+ c[u], u N \ N '

v[ j(u)] = min{v[i(u)]+ c[u], u N+j } (*) Является вектором кратчайших длин путей.

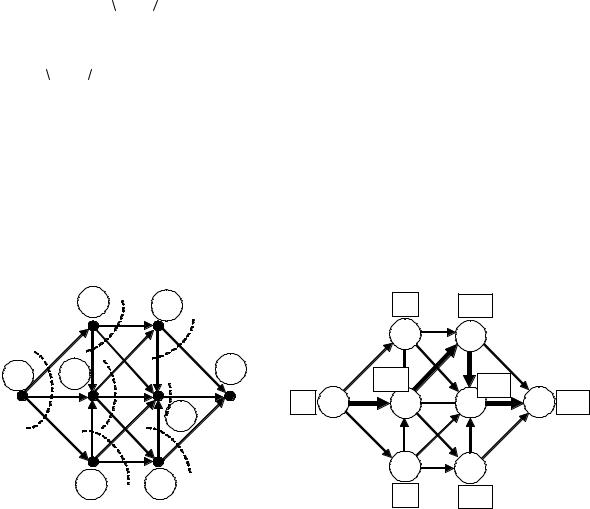
Метод потенциалов для задачи о кратчайших путях несколько видоизменяется. Вопервых, нет смысла считать потоки по базисному дереву. Их структура совершенно ясна. Поток убывает на единицу с каждой пройденной дугой по мере удаления от i0 и равен единице на последней дуге каждой ветви дерева (числа в кружках – номера вершин).

		2	4			1	4	7
						1	4	7
			2				(2)	(1)
1	1	3	2
1	1	3		2	(3)
		3		2
		3
i0	2	2	3			2	5	8
i0					(3)	2	5	8
					(3)		(2)	(1)
	1	2	1		i0
2	1	2	1	3
2		3		3
					(3)	3	6	9
		2	3				(2)	(1)

При вычислении потенциалов, здесь всегда потенциал конца дуги вычисляется по потенциалу начала дуги.

1	3		7		1	3	7
		2		2
2	4	u	7	u	2	4	5
0				i0	0
2	4		7		2	2	7

Это дерево кратчайших путей

Вводимая в базис дуга u порождает цикл, состоящий из двух путей различной ориентации, идущих из i0 в конец дуги u . Из базиса удаляется дуга " отрицательной " части цикла, примыкающая к концу дуги u . Потенциалы пересчитываются для всех вершин, следующих за j(u ): они уменьшаются на одну и ту же величину

ε [u] = v[ j(u)]− v[i(u)]− c[u].

Одним из самых эффективных алгоритмов реализации метода потенциалов в данной задаче при положительном векторе c[N] (что, вообще говоря, не требуется при постановке задачи) является алгоритм Дейкстры

209

2. Критический путь (задача о максимальном пути)

Дан связный граф M, N без контуров, t[N]≥ 0[N] – вектор длин дуг. В графе выделены

две вершины i− и i+ . Требуется найти путь из i− в i+ , имеющий наибольшую длину.

Если M, N – сетевой график выполнения некоторого проекта ( M – множество

событий, i− – начальное событие проекта, i+ – конечное событие проекта, N – множество работ проекта, t[N] – время их выполнения), то нахождение самого длинного пути из i−

в i+ (такой путь в сетевом планировании называется критическим) определяет минимально возможное время выполнения всего проекта

Изменением знаков у t[u] возможно свести нашу задачу к поиску кратчайшего пути, но

можно не пользоваться алгоритмом поиска кратчайших путей, а, вводя "правильную" нумерацию вершин (по алгоритму Форда) найти потенциалы за один проход по правилу

(*) , изменяя в нем min на max . Рассмотрим пример.

(1)

(2)
	5						2		18
		(5)					2	4	5
							2		5
								6	6	5
								4		5
	(7)	8						4
		8				10
(4)						10		8		24
(4)		i+				5		8		24
		i+	0	1		5	4		7	8	28
			0	1			4	9	7	8	28
	7							9		4
	7
					7	3			4
						3		7
								7		5
								10		5
								10
	6	(6)					3		6
(3)	6						7		17

В соответствие с алгоритмом Форда в сети отыскивается вершина, в которую не входит ни одна дуга ( Ni+ = . Первая такая вершина i− – начальное событие проекта). Она получает

очередной номер и удаляются все дуги из нее выходящие. Процесс продолжается до исчерпания множества вершин. Имеем граф с "правильной" нумерацией и заданными длинами дуг t[N].

Применяем правило вычисления потенциалов.

v[1]= 0,

{

(

)

[

]

j }

[

]

= max

+ t

, u N

v[2]= v[1]+ 2 = 0+ 2 = 2

v[3]= v[1]+ 7 = 0+ 7 = 7

[ ]

}

{

}

[

]

= max

{

[ ]

+ 5,v

[

]

+ 4,v

= max

0 +

[

{

[

]

+ 3

5,2+ 4,7 + 3

=10

]

= max

+ 4,v

[

]

}

= max

{

+ 4,10+

}

=18

[

]

{

[

+ 8

= max

]

+ 8,v

]

}

= max

{

+ 8,10 +

}

=17

[

]

{

[

]

+ 7

{

}

= max

+ 6,v

[ ]

+ 3,v

[

]

+ 3,v

[

]

+ 6,v

[

]

}

= max

= 24

+ 4

+ 6,7 + 3,10 + 3,18+ 6,17 + 4

[

]

= max

{

[

]

+ 9,v

[

]

+ 5,v

[

]

}

{

}

+ 4

= max 18+ 9,17 + 5,24+ 4 = 28

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2821 22 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016327.17 Кб77Думин И.В. Другая Русь.doc
#
29.03.2016114.03 Кб212Е.А. Шевченко УМКРУНТ фольклор русский.docx
#
28.03.2016159.74 Кб82Евгений Онегин статья Маймина.doc
#
28.03.2016748.03 Кб16Еколе русс.doc
#
26.09.2019454.66 Кб35Загайнов Рудольф Максимович Психологическое мас...doc
#
29.03.20167.61 Mб29Зад лин прогр и мет их решения 16 12 08.pdf
#
29.03.2016470.27 Кб20Задания для самостоятельной работы.pdf
#
28.03.201646.84 Кб26Задания о выпуске продукции при ограниченных ресурсах.docx
#
28.03.2016152.06 Кб16Задачи к экзамену.doc
#
29.03.20167.64 Mб155Задачи ЛП и методы их решения .pdf
#
23.11.2018455.17 Кб9ЗАДАЧИ СОКОЛОВ!!!.doc

		2	4			1	4	7
						1	4	7
			2				(2)	(1)
1	1	3	2
1	1	3		2	(3)
		3		2
		3
i0	2	2	3			2	5	8
i0					(3)	2	5	8
					(3)		(2)	(1)
	1	2	1		i0
2	1	2	1	3
2		3		3
					(3)	3	6	9
		2	3				(2)	(1)

(2)
	5						2		18
		(5)					2	4	5
							2		5
								6	6	5
								4		5
	(7)	8						4
		8				10
(4)						10		8		24
(4)		i+				5		8		24
		i+	0	1		5	4		7	8	28
			0	1			4	9	7	8	28
	7							9		4
	7
					7	3			4
						3		7
								7		5
								10		5
								10
	6	(6)					3		6
(3)	6						7		17

		2	4			1	4	7
						1	4	7
			2				(2)	(1)
1	1	3	2
1	1	3		2	(3)
		3		2
		3
i0	2	2	3			2	5	8
i0					(3)	2	5	8
					(3)		(2)	(1)
	1	2	1		i0
2	1	2	1	3
2		3		3
					(3)	3	6	9
		2	3				(2)	(1)

(2)
	5						2		18
		(5)					2	4	5
							2		5
								6	6	5
								4		5
	(7)	8						4
		8				10
(4)						10		8		24
(4)		i+				5		8		24
		i+	0	1		5	4		7	8	28
			0	1			4	9	7	8	28
	7							9		4
	7
					7	3			4
						3		7
								7		5
								10		5
								10
	6	(6)					3		6
(3)	6						7		17

		2	4			1	4	7
						1	4	7
			2				(2)	(1)
1	1	3	2
1	1	3		2	(3)
		3		2
		3
i0	2	2	3			2	5	8
i0					(3)	2	5	8
					(3)		(2)	(1)
	1	2	1		i0
2	1	2	1	3
2		3		3
					(3)	3	6	9
		2	3				(2)	(1)

(2)
	5						2		18
		(5)					2	4	5
							2		5
								6	6	5
								4		5
	(7)	8						4
		8				10
(4)						10		8		24
(4)		i+				5		8		24
		i+	0	1		5	4		7	8	28
			0	1			4	9	7	8	28
	7							9		4
	7
					7	3			4
						3		7
								7		5
								10		5
								10
	6	(6)					3		6
(3)	6						7		17