
Зад лин прогр и мет их решения 16 12 08
.pdf
190
Вывод: Полученное решение (с учетом брака шириной 6L ) "не хуже" оптимального решения без брака (т.к. 65+ 6 = 71, т.е. в отходы ушел только брак).
Раскрой при наличие случайного брака на тамбуре
Исходные данные: L |
– ширина тамбура |
|M| |
- число форматов |
|N| |
- число раскладок |
l[M] – вектор ширин форматов |
|
b0[M] – вектор требований на форматы
Исходная ситуация: Решена целочисленная задача форматного раскроя при заданном векторе требований b[M]. В результате получен набор оптимальных
|
раскладок A[M,N0] и целочисленный вектор интенсивностей их |
|||||
|
использования x[N0]. При разрезании очередного съёма на ПРС |
|||||
|
несколько рулонов оказываются бракованными. Необходимо |
|||||
|
поставить новую задачу целочисленного форматного раскроя, |
|||||
|
изменив вектор требований с учетом уже нарезанных рулонов и |
|||||
|
полученного брака. |
|
|
|
||
Пусть |
bˆ[M ] - вектор количества нарезанных рулонов (по форматам), а |
|
|
|
||
b[M ]- вектор |
||||||
|
Тогда bɶ[M ] = bˆ[M ]− |
|
[M ] - выполненная часть вектора |
|
||
брака. |
b |
требований, а |
||||
b [M ] = b [M ]− bɶ[M ] - текущий остаток вектора требований |
|
|
|
|||
1 |
0 |
|
|
|
|
|
(новый вектор требований).
Формулируем новую целочисленную задачу форматного раскроя при тех же исходных данных и новом векторе требований b1[M ]. Решаем её, и продолжаем разрезание по новому графику (вообще говоря, новый оптимальный набор раскладок и новый вектор
интенсивностей их использования). |
|
|
|
||
Алгоритм решения: |
|
|
|
||
(0) |
k:=0 |
|
|
|
A[M, N0 ] x[N0 ] = bk [M ] |
|
f (x) = 1[N] x[N] → min |
|
МСМ+ПЕРЕБОР |
||
(1) |
|
|
|
|
x[N \ N0 ] = 0[N \ N0 ] |
|
A[M, N] x[N] = bk [M ] |
|
|
||
|
|
x[N] ≥ 0, целочисл. |
|
|
N0 = { j1, j2 ,..., js} |
|
|
|
|
|
|
(2) Отрезаем очередной съём A[M, jp ]. ( p1: s). |
|
|
||
Если |
|
[M ] = 0[M ] (на съёме нет брака), то bɶ[M ] = A[M, j |
|
], и |
b |
p |
|||
|
|
|
|
|
s
∑ A[M, jk ] X[ jk ]+ A[M, jp ](X[ jp ]−1) = bk [M ]− A[M, jp ], иначе на шаг (4)
k=1
k≠ jp
(3)В этом случае график резания не меняем.
bk [M ]:= bk [M ]− A[M, jp ], X[N0 ]:= X[N0 ]− (0,...,0,1,0,...,0).
j p
Переходим на шаг (2).
(4) Если b[M ] ≠ 0[M ], то bk+1[M ]:= bk [M ]− A[M, jp ]+ b[M ], j0 := jp (Запоминаем раскладку, по которой вырезали последний съём) k := k +1. Переходим к шагу (1)
Выше описан алгоритм решения при наличии заказа в посъёмном режиме. Можно предложить модификацию этого алгоритма, заключающегося в другой последовательности решения целочисленных задач форматного раскроя. Сначала нарезаем вектор b0[M], а вектор брака b[M ] только учитываем суммированием

192
3. В 7-м съёме (19 от начала) брак 3го формата (одного рулона)
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|||
b = |
9 |
− |
8 |
+ 0 |
- это способ раскроя с остатком 6. |
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
25 |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Всего вырезано 20 съёмов. (остаток 7). |
|
||||||||||||
|
1 |
|
0 |
|
0 |
|
|
0 |
11 |
10 |
1 |
||
11 |
1 |
+ 7 |
1 |
+1 |
2 |
+1 |
1 |
= 21 |
= 20 |
+ 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
|
1 |
41 |
40 |
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
(6) |
|
|
|
|
Модификация даёт такой же результат.
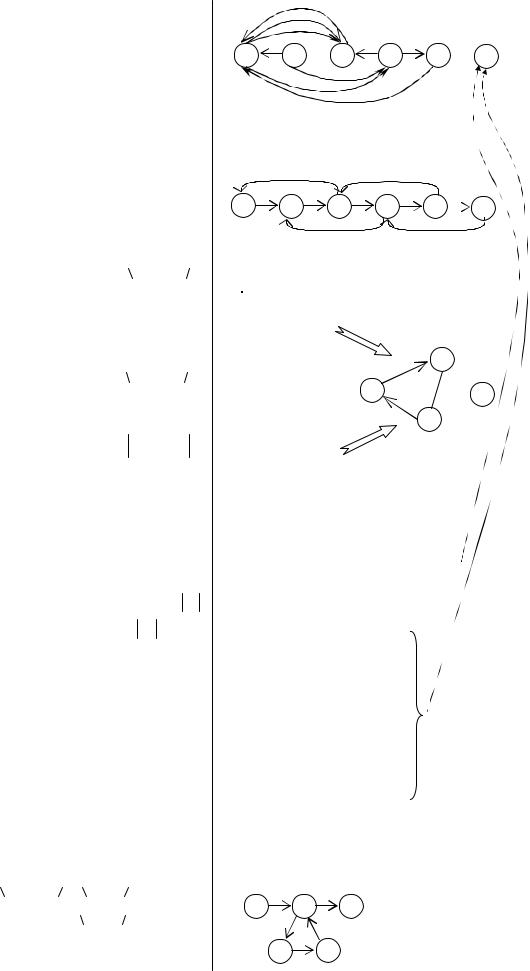
Рассмотренные выше особенности постановки и решения задач линейного целочисленного раскроя применительно к форматному раскрою бумажного полотна показывают тесные и многообразные взаимосвязи задач линейного и целочисленного программирования с самыми различными задачами исследования производственных операций.

197
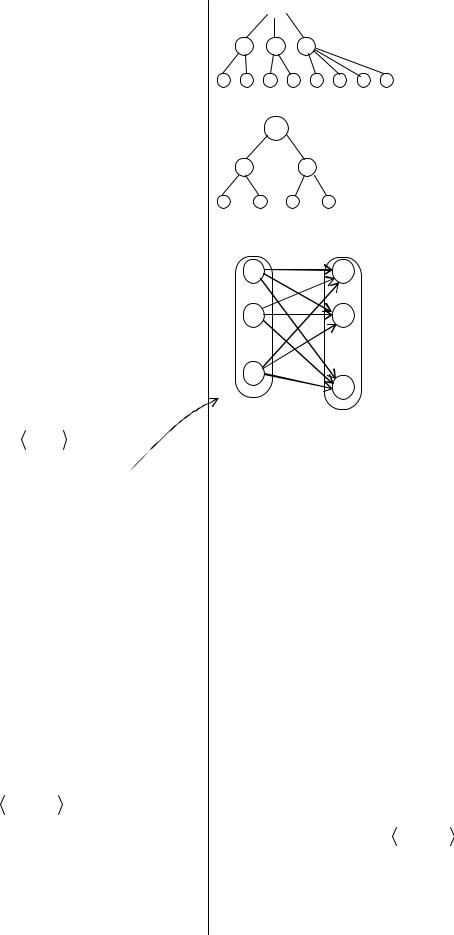
 корень
корень
иерархическое дерево
|
|
|
|
|
|
|
|
|
бинарное дерево |
|
|
|
|
|
|
|
|
|
|||
7.14.2. Постановка сетевой |
K |
C[1,1] |
L |
∑ |
C i, j |
x i, j |
→m |
||||||||||||||
транспортной задачи |
|
|
|||||||||||||||||||
|
|
1 |
1 |
[ |
|
] |
[ |
|
] |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
i K,j L |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x i, j |
=αi |
,i K |
||||||
а) Матричная транспортная задача (ТЗ) |
|
|
|
|
|||||||||||||||||
|
|
|
∑ |
[ |
] |
|
[ ] |
|
|
|
|||||||||||
К – множество пунктов производства |
2 |
|
2 |
j L |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
( i K, |
α[i]>0 - объем производства) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
∑x[i, j]=β[j], j L |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i K |
|
|
|
|
|
|
|
|||
L – множество пунктов потребления |
|
|
|
|
|
|
≥0 K,L |
|
|||||||||||||
m |
|
|
x K,L |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
[ |
] |
|
|
[ |
|
] |
|
||
( j L, |
β[j]>0 |
- объем потребления) |
|
C[m,n] |
n |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
C[i, j] - матрица цен перевозок |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
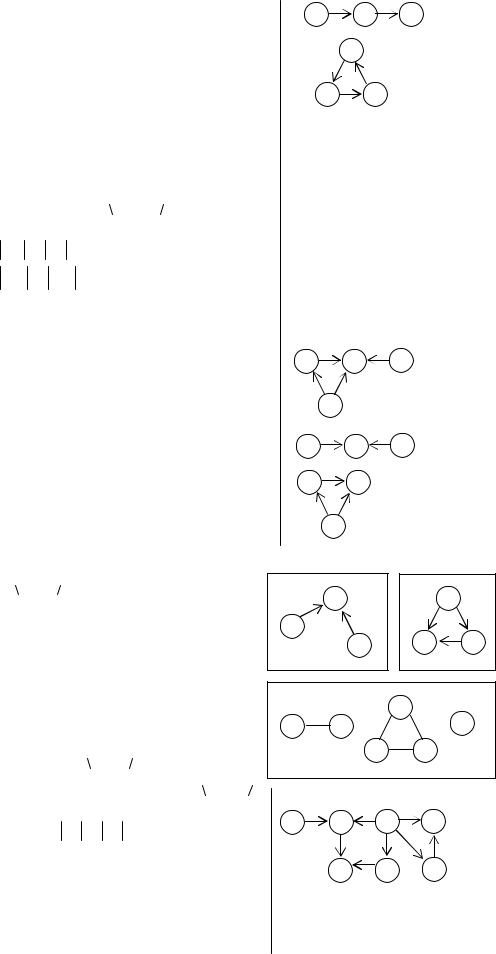
Рассмотрим граф |
M, N : |
|
|
|
C[N ] x[N ]→ min |
|
|
|
|
|
|
|
|
|
|||||||
1. M = K L, (K ∩L = ) |
|
|
|
|
|
|
|
− |
= ) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
(*) |
∑u Ni+ x[u]=b[i], i L. (Ni |
|
||||||||||
2. |
N = K×L, ( u N i(u) K, j(u) L) (**) −∑u Ni− x[u]=b[i], i K. (Ni+ = ) |
||||||||||||||||||||
|
(такой граф называется двудольным) |
|
x[N ]≥0[N ] |
|
|
|
|
|
|
|
|
|
|||||||||
Теперь вместо матриц C и X можно |
|
|
|
|
|
|
|
|
|
|
|||||||||||
рассмотреть векторы |
|
C[N ] |
и X [N] и для |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
удобства, считать, что |
|
|
|
|
Условия (*) и (**) теперь можно переписать |
||||||||||||||||
|
|
|
|
в виде |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
[ |
] |
>0, |
i |
L |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
b[i] |
|
β i |
|
(+) |
∑u Ni+ x[u]−∑u Ni− x[u]=b[i], i M |
||||||||||||||
|
|
= |
|
|
|
|
|
||||||||||||||
|
|
|
−α[i]<0, i K. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие (+) можно трактовать, как баланс |
|
C[N ] x[N ]→ min |
|
|
|
|
|
|
|
|
|
||||||||||
потока груза: для каждой вершины разность |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
втекающего и вытекающего потоков равна |
(*) |
∑u Ni+ x[u]=b[i], |
i L. (Ni− = ) |
|
|||||||||||||||||
потреблению. Теперь нам надо искать такой |
(**) −∑u Ni− x[u]=b[i], |
i K. (Ni+ = ) |
|||||||||||||||||||
сбалансированный для всех вершин поток с |
|||||||||||||||||||||
максимальной стоимостью. |
|
|
x[N ]≥0[N ] |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
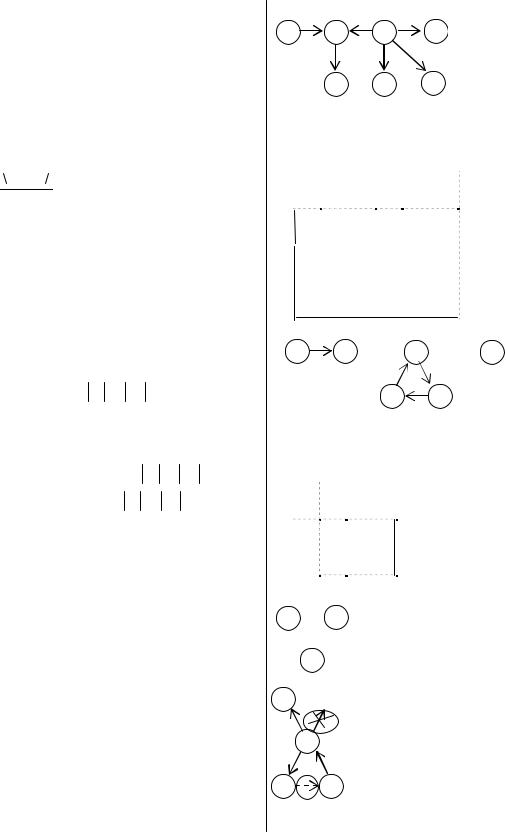
Сетевая транспортная задача (СТЗ) |
В такой постановке устранены особенности |
||||||||||||||||||||
конкретного графа и ТЗ может быть |
|||||||||||||||||||||
Задан |
граф |
M, N,T , |
представляющий |
||||||||||||||||||
собой транспортную сеть, узлами которой |
поставлена для |
произвольного |
связного |
||||||||||||||||||
ориентированного графа |
M, N,T . |
|
|
|
|
||||||||||||||||
являются вершины M , в которых задано |
Рассмотрим основной пример. |
|
|
|
|
|
|
|
|||||||||||||
потребление. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Пусть |
задана |
транспортная |
|
|
сеть |
|
с |
||||||||
|
>0−потребитель |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
исходными данными (числа у вершины – |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
b[i]= |
|
0−производитель |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
< |
|
объемы потребления, у каждой дуги – цены |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
0−промежуточный пункт |
перевозок). |
|
|
|
|
|
|
|
|
|
|
||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

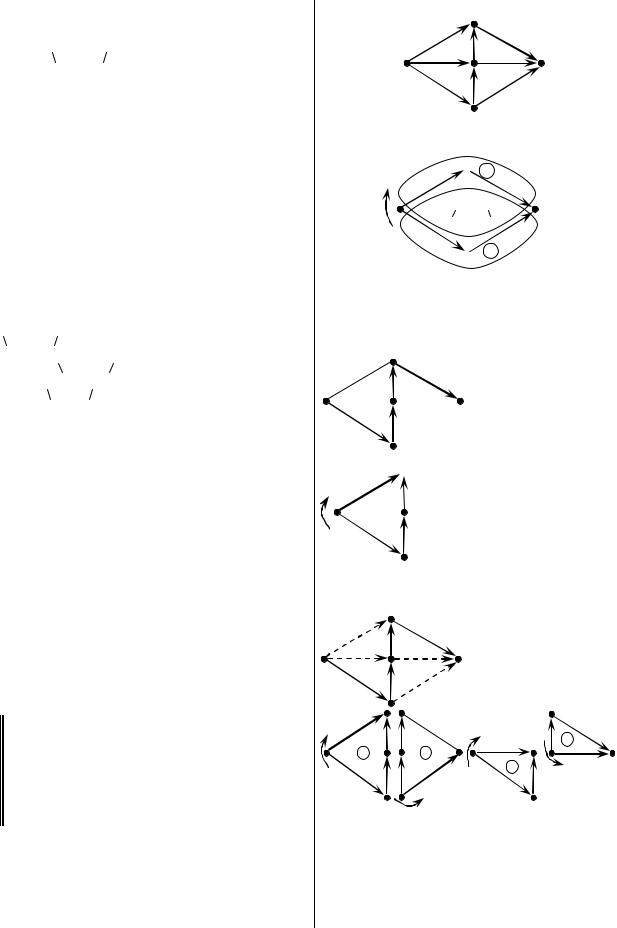



 M
M

 - это
- это i
i 









 - пара
- пара
 называется контуром если:
называется контуром если:
 называется
называется 
 можно выделить
можно выделить



 - цепь (дерево)
- цепь (дерево) нарушение связности
нарушение связности
 - цикл с заданной на нем
- цикл с заданной на нем M
M 

 связывающее дерево в графе
связывающее дерево в графе 
 . Цикл, в котором только одна
. Цикл, в котором только одна +
+ M
M 
 −
− 3
3