
Зад лин прогр и мет их решения 16 12 08
.pdf
30
В строке |
все оценки положительны или равны нулю. Следовательно, выполняются |
|
условия оптимальности |
|
|
|
j ≥ 0 |
( j 1: n) |
Таким образом, мы заключаем, что текущее решение является оптимальным |
решением |
ЗЛП (т.е. целевая функция достигла своего максимального значения fmax =108/ |
5). |
Выпишем оптимальное значение из симплекс-таблицы. В столбце NБ хранятся номера базисных переменных, а в столбце ХБ их значения.
Получаем
NБ XБ
2 |
12/5 |
1 |
12/5 |
5 |
16/5 |

 x2 = 12/5
x2 = 12/5


 x1 =12/5
x1 =12/5 


 x5 = 16/5
x5 = 16/5 

Остальные переменные (небазисные) равны нулю: x3 = 0, x4 = 0
Значение целевой функции выписываем из клетки f f = 108 / 5
Окончательно, данная ЗЛП имеет следующее оптимальное решение:
X* =( |
12 |
, |
12 |
, 0 , 0, |
|
16 |
), f (X*)=108/ 5 |
|
|
|
5 |
|
5 |
||||
5 |
|
|
|
|||||
Такой же результат получен графически (см. раздел 2 ) ЭКОНОМИЧЕСКИЙ СМЫСЛ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ.
1.Наиболее выгодным является выпуск табуреток и стульев в количестве по 12 шт. за 5 плановых периодов.
2.Прибыль за плановый период составит 108\5 ед.
3.Сырье 1-го и 2-го видов при этом будет израсходовано полностью ( x3 = 0, x4 = 0), а остаток сырья 3-го вида ( x5 ) составит 16\5 ед. к концу планового периода.
31
3.4. Метод искусственных переменных. Вспомогательная задача ЛП.
В рассмотренном выше примере столбцы матрицы ограничений при дополнительных переменных x3, x4, x5 образовывали единичную подматрицу
|
1 |
|
|
0 |
|
|
0 |
|
|
1 0 |
0 |
||||
A3 = |
|
|
|
A4 = |
|
|
|
A5 = |
|
|
|
AБ = |
|
|
|
0 |
, |
1 |
, |
0 |
, |
0 |
1 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
1 |
|
|
0 |
1 |
||||
Выбирая дополнительные переменные в качестве базисных легко получить начальное базисное решение
x3 = 24 , x4 =12, x5 = 8 - значения базисных переменных равны соответствующим элементам вектора правой части в системе ограничений;
x1 = 0, x2 = 0- значения небазисных переменных равны нулю;
и заполнить начальную симплекс-таблицу.
В общем случае (например для ЗЛП в стандартной форме)
f = x1 − 2x2 + 4x3 + 6x4 → max
|
x + x |
+ x |
+ x |
= 2 |
|
|
1 |
2 |
3 |
4 |
(+) |
2x1 − x2 − x3 + 2x4 = 4 |
|||||
|
xi |
≥ 0 |
(i 1: 4) |
||
для нахождения начального базисного решения и заполнения начальной симплекс-таблицы необходимо проделать следующее:
а) Выбрать столбцы матрицы ограничений, составляющую квадратную матрицу (их число должно быть равно числу ограничений).
Например
A1 = |
1 |
|
|
|
1 |
|
|
1 |
1 |
|
|
, |
|
A2 |
= |
|
, |
AБ |
= |
|
( * ) |
||
|
|
2 |
|
|
−1 |
|
|
2 |
−1 |
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
1 |
|
A2 |
= |
|
, |
A3 |
= |
|
, |
AБ |
= |
|
( ** ) |
|
−1 |
|
|
−1 |
|
|
−1 |
−1 |
|
||
б) Убедиться в том, что они (выбранные столбцы) образуют базис (путем нахождения обратной матрицы), либо установить их линейную зависимость.
Так, столбцы A2 и A3 не образуют базис в силу их линейной зависимости (в данном случае они просто равны между собой), а матрица в (**) не является базисной. С другой стороны, столбцы A1 и A2 линейно независимы (они не пропорциональны друг другу) и обратную матрицу к базисной в (*) можно найти путем приведения исходной базисной матрицы к единичной по методу полного исключения Гаусса-Жордана.
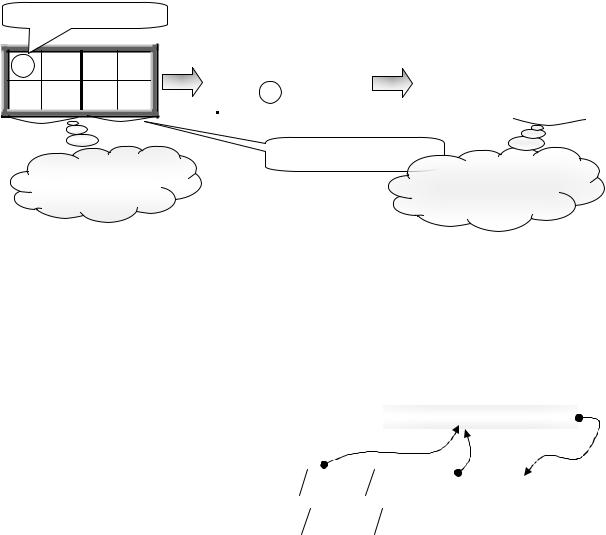
32
Это ведущий элемент
1 |
1 |
1 |
0 |
2 |
-1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
1 |
0 |
1/3 |
1/3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-3 |
-2 |
1 |
|
|
0 |
1 |
2/3 |
-1/3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это единичная матрица |
Это исходная |
Это матрица обратная |
базисная матрица |
к базисной |
в) Найти значения базисных компонент ( x1 , x2 ) начального базисного решения и убедиться в его допустимости, т.е. проверить выполнение ограничений неотрицательности). Для этого необходимо умножить найденную обратную матрицу
1 |
1 |
|
||||||
|
|
|
|
|
|
|
||
3 |
3 |
|||||||
B = |
|
|||||||
|
|
2 |
− |
1 |
|
|||
|
|
|
||||||
3 |
3 |
|
||||||
на вектор правой части b = [2 4] |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перемножаются скалярно |
|
|
|
|
|
|
|
|
|
|
x |
|
1 3 |
1 3 |
2 |
2 |
|
|
|
= |
|
|
= |
|
x |
|
|
2 3 |
−1 3 |
4 |
0 |
Начальное базисное решение X0 |
= (2, 0, |
0, 0) является допустимым, т.к. все его |
||||
компоненты неотрицательны. |
|
|
|
|
|
|
г) Перед заполнением начальной симплекс-таблицы (т.к. выбранный базис
{A1 , A2 }отличается от единичного) требуется вычислить матрицу разложения всех столбцов исходной системы ограничений по данному базису. Для этого необходимо умножить обратную матрицу В на матрицу исходной системы ограничений,
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1/3 |
1/3 |
Х |
1 |
1 |
1 |
1 |
= |
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
2/3 |
-1/3 |
|
2 |
-1 |
-1 |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее симплекс-таблица заполняется обычным образом (см. 3.3) и приобретает следующий вид
33
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
NБ CБ XБ |
|
|
|
|
|
|
|
||||
1 |
-2 |
4 |
6 |
|
C |
||||||
1 |
1 |
2 |
|
|
|
0 |
|
1 |
|
|
|
|
1 |
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
-2 |
0 |
|
0 |
1 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
0 |
-6 |
-5 |
f |
|
|
|
|
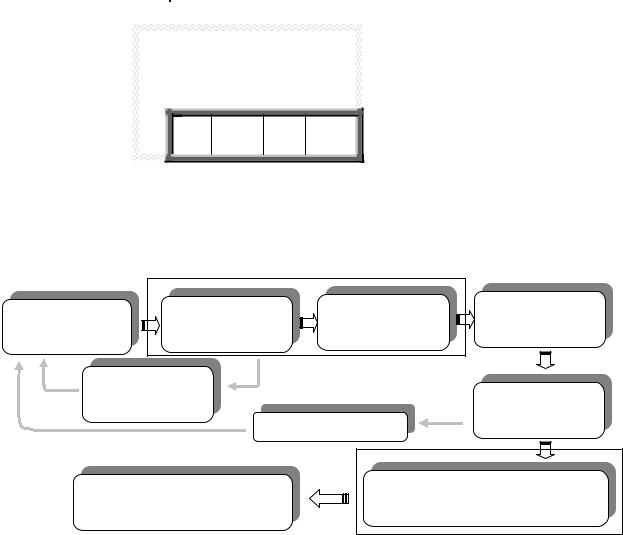
Теперь текущее базисное решение может быть улучшено посредством симплекс-алгоритма. Из приведенного примера видно, что при отсутствии единичного базиса в исходной
системе ограничений ЗЛП требуется значительная вычислительная работа для выполнения нулевого шага симплекс-метода.
Выбор |
Установление их |
Нахождение |
Определение |
|
линейной |
обратной |
базисных компонент |
||
столбцов |
||||
независимости |
матрицы |
решения |
||
|
Столбцы линейно зависимы
Окончательное заполнение начальной симплекс-таблицы
|
Проверка |
|
выполнения условий |
Решение недопустимо |
неотрицательности |
Вычисление матрицы разложения |
|
|
столбцов по базису |
Основные вычислительные действия заключены в выделенных элементах схемы. Кроме того процесс может оказаться итерационным, т.е. потребовать повторений при выборе линейно зависимых столбцов или при получении начального решения, не являющегося допустимым (среди базисных компонент которого есть отрицательные).
Этой громоздкой процедуры можно избежать, если предварительно рассмотреть следующую вспомогательную задачу ЛП:
f =
|
x + x + x + x + x |
= 2 |
||||
|
1 |
2 |
3 |
4 |
5 |
(i) |
2x1 − x2 − x3 + 2x4 |
+ x6 |
= 4 |
||||
|
xi ≥ 0 |
|
(i 1:6) |
|
|
|
Переменные x5 и x6 в задаче ЛП (i) носят название искусственных переменных. Задача (i)
имеет начальное базисное решение с единичным базисом, соответствующим искусственным переменным
X i |
= (0, 0, 0, 0, 2, 4) |
0 |
|

34
и ее целевая функция ограничена снизу нулем. А, следовательно, такая задача ЛП всегда разрешима.
Пусть X * = (x1* , x2* , x3* , x4* , x5* , x6* ) оптимальное решение задачи (i),
а g(X * ) - минимальное значение целевой функции. Если при этом g(X * ) = 0 и
искусственные переменные x5 , x6 , не входят в число базисных ( x5* = 0, x6* = 0 ), то
X0 = (x1* , x2* , x3* , x4* )
является начальным базисным решением исходной ЗЛП (+).
Построение начальной симплекс-таблицы для ЗЛП (i) трудностей не вызывает, т.к.
начальное решение имеет единичный базис. |
|
|
|
|
|||||||
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NБ |
CБ |
XБ |
0 |
0 |
0 |
0 |
1 |
1 |
C Улучшаем данное решение в |
|
5 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
0 |
|
соответствии с алгоритмом |
|
|
симплекс-метода для ЗЛП на |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min (заметим, что изменяется |
6 |
1 |
4 |
2 |
-1 |
-1 |
2 |
0 |
1 |
|
||
|
только критерий оптимальности |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
0 |
0 |
3 |
0 |
0 |
j ≤ 0, j 1:6 ) |
f
ШАГ 1. |
1 |
> 0. Текущее решение не является оптимальным. |
|||||||||||
|
|
|
Бi |
|
|
|
|
2 |
|
4 |
|
|
|
|
|
x |
|
|
|
|
|
||||||
ШАГ 2. |
j0 |
=1, θ = min |
|
|
|
Aj i |
> 0 |
= min |
|
, |
|
|
= 2 |
|
|
1 |
2 |
||||||||||
|
|
A |
|
|
0 |
|
|
|
|
|
|||
|
|
|
j0i |
|
|
|
|
|
|
|
|
|
|
ШАГ 3. Переходим к новому базисному решению с базисом {5, 1}.
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
NБ CБ XБ |
|
|
|
|
|
|
||
0 |
0 |
0 |
0 |
1 |
1 |
|||
|
|
|
|
|
|
|
|
|
5 |
1 |
0 |
0 |
3/2 |
3/2 |
0 |
1 |
-1/2 |
|
|
|
|
|
|
|
|
|
1 |
0 |
2 |
1 |
-1/2 |
-1/2 |
1 |
0 |
1/2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
3/2 |
3/2 |
0 |
0 |
-3/2 |
|
|
|
|
|
|
|
|
|
ШАГ 1. |
2 |
> 0 . Текущее решение не является оптимальным. |
|||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
ШАГ 2. |
j0 |
= 2 |
, θ = min |
|
|
= 0 |
|
3 |
|||||||
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
ШАГ 3. Переходим к новому базисному решению с базисом {2, 1}.
35
1 |
-2 |
4 |
6 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
NБ CБ XБ |
0 |
0 |
0 |
0 |
1 |
1 |
|
||
2 |
0 |
0 |
0 |
1 |
1 |
0 |
2/3 |
-1/3 |
|
1 |
0 |
2 |
1 |
0 |
0 |
1 |
1/3 |
1/3 |
|
|
|
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
Полученное решение |
|
|
ЗЛП (*) является |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оптимальным |
Если теперь отбросить часть С-Т, относящуюся к искусственным переменным, заменить коэффициенты в целевой функции из ЗЛП (+) и пересчитать последнюю строку (значение целевой функции и оценки), то получим С-Т для улучшения начального базисного решения
X0 = (2, 0, 0, 0)
исходной ЗЛП (+).
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
NБ CБ XБ |
|
|
|
|
|
|
|
|
|||
1 |
-2 |
4 |
6 |
|
|
C |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
-2 |
0 |
|
|
1 |
|
0 |
|
|
Действуем далее в соответствии с |
|
0 |
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
1 |
0 |
0 |
|
1 |
|
|
алгоритмом С-М для задачи на |
|
|
|
|
максимизацию. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0 0 -6 -5
f
ШАГ 1. 3 < 0 . Текущее решение не является оптимальным.
|
|
0 |
|
|
||
ШАГ 2. |
j0 |
= 3, θ = min |
|
|
= 0 |
|
1 |
||||||
|
|
|
|
|
||
ШАГ 3. Переходим к новому базисному решению с базисом {3, 1}.
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
NБ CБ XБ |
1 |
-2 |
4 |
6 |
C |
|
|
|
|
|
|
3 |
4 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
2 |
1 |
0 |
0 |
1 |
|
|
2 |
0 |
6 |
0 |
-5 |
f
36
ШАГ 1. |
4 |
< 0. Текущее решение не является оптимальным. |
||||
|
|
= 4 |
2 |
|
|
|
ШАГ 2. |
j0 |
, θ = min |
|
|
= 2 |
|
|
||||||
|
|
|
1 |
|
|
|
ШАГ 3. Переходим к новому базисному решению с базисом {3, 4}.
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
NБ CБ XБ |
|
|
|
|
|
|
||||
1 |
-2 |
4 |
6 |
|
||||||
3 |
4 |
0 |
|
|
|
1 |
|
0 |
|
|
|
0 |
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
2 |
|
1 |
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
5 |
6 |
0 |
0 |
f |
|
|
|
|
C
ШАГ 1. Текущее решение является оптимальным, т.к.
j ≥ 0, j 1: 4
Если в оптимальном решении задачи (i) g(X*i ) > 0 , то это соответствует
неразрешимости исходной ЗЛП (+), из-за отсутствия допустимых решений.
Действительно, если
X0 = (x10 , x20 , x30 , x40 )- допустимое решение ЗЛП (+), то
X0i = (x10 , x20 , x30 , x40 ,0,0) -допустимое решение ЗЛП (i). При этом
g(X0i ) = 0 < g(X*i ) = gmin - противоречие !!!.
Значит ЗЛП (+) не имеет ни одного допустимого решения.
В качестве примера рассмотрим ЗЛП
f = x1 + 2x2 + x3 → max
2x |
+ 3x |
|
+ 5x |
|
= 30 |
|
|
1 |
|
2 |
|
3 |
( + ) |
6x1 + 9x2 |
+15x3 = 91 |
|||||
|
|
xi ≥ 0 , |
|
(i 1: 3) |
||
Воспользуемся методом искусственных переменных и запишем вспомогательную задачу ЛП.
f = x4 + x5 → min
2x + 3x |
|
+ 5x |
|
+ x |
|
= 30 |
||
|
1 |
|
2 |
|
3 |
|
4 |
( i ) |
6x1 + 9x2 |
+15x3 |
|
+ x5 = 91 |
|||||
|
xi |
≥ 0 |
(i 1: 5) |
|||||
37
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
NБ CБ XБ |
0 |
0 |
0 |
1 |
1 |
C |
NБ CБ XБ |
0 |
0 |
0 |
1 |
1 |
||||
4 |
1 |
30 |
2 |
3 |
5 |
1 |
0 |
|
1 |
0 |
15 |
1 |
3/2 |
5/2 |
1/2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
1 |
0 |
0 |
0 |
-3 |
1 |
5 |
1 |
91 |
6 |
9 |
15 |
0 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
-4 |
0 |
|
|
121 |
8 |
12 |
20 |
0 |
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Текущее решение является оптимальным решением задачи (i) и gmin =1> 0. Следовательно, исходная ЗЛП(+) не имеет ни одного допустимого решения. Действительно, левая часть 2-го уравнения в системе ограничений ЗЛП (+) может быть получена, если 1-ое уравнение умножить на 3. Тогда имеем
6x1 + 9x2 +15x3 = 906x1 + 9x2 +15x3 = 91
Ясно, что данная система несовместна. h
38
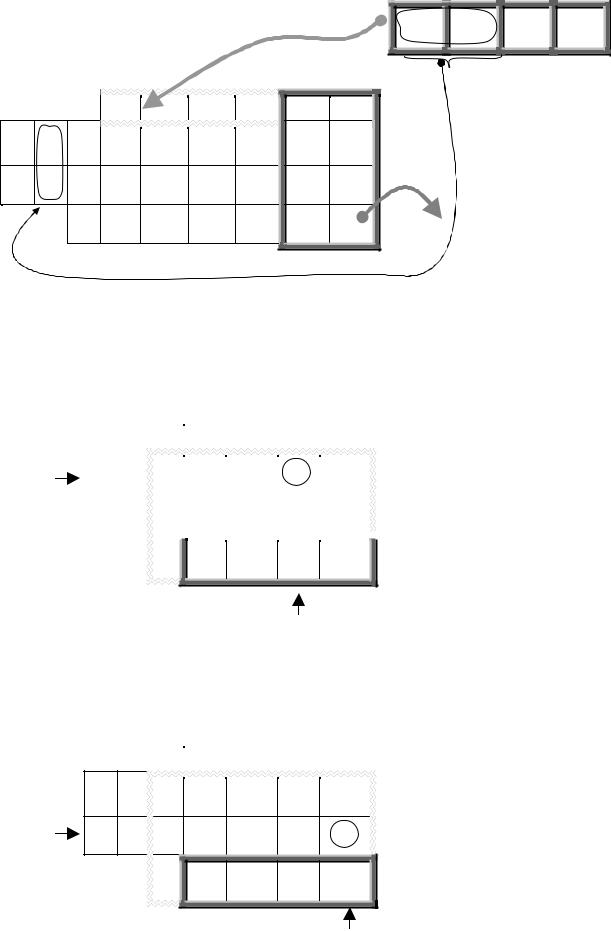
4. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
Рассмотрим частный случай задачи линейного программирования, которая получила название транспортной задачи (ТЗ). Модификация симплекс-метода для ее решения называется методом потенциалов.
|
4.1 Постановка транспортной задачи. |
|
|
|
|
|
|
||
|
|
Потребность |
Пусть |
имеется |
несколько |
||||
|
|
|
|
|
|
|
|
||
|
Цена |
в |
поставщиков |
однородной |
|||||
|
продукции |
продукции |
|
(каждый |
с |
||||
|
перевозки |
|
|||||||
|
|
|
|||||||
Запас |
|
60 |
определенным |
запасом) |
и |
||||
продукции |
|
несколько |
|
потребителей |
этой |
||||
|
5 |
|
|
||||||
|
|
продукции |
(с |
известными |
|||||
|
120 |
|
|||||||
|
|
|
|
|
|
|
|
||
|
10 |
|
потребностями |
у |
каждого). |
||||
|
12 |
|
|||||||
|
100 |
Задана |
|
также |
|
сеть |
|||
|
|
|
|
||||||
|
8 |
|
коммуникаций |
(дорог, |
рек, |
||||
|
6 |
|
воздушных |
линий |
и |
т.д.), |
|||
|
70 |
|
|||||||
|
80 |
связывающая |
|
каждого |
|||||
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
||
Это |
|
|
поставщика |
с |
каждым |
||||
Это |
|
|
|
|
|
|
|
||
поставщики |
|
потребителем. |
На |
каждой |
|||||
коммуникации |
Это |
||||||||
|
коммуникации |
задана |
цена |
||||||
|
|
потребители |
|||||||
|
|
|
перевозки |
|
- |
|
стоимость |
||
|
|
|
перевозки |
|
единицы |
продукции |
|||
(см. рис.). |
|
|
|
|
|
|
|
|
|
Если какая-либо коммуникация отсутствует, то считаем, что она есть, но цену перевозки на ней устанавливаем равной бесконечности (+ ∞ ). Это соглашение сделает невыгодным перевозку по ней и автоматически исключит данную коммуникацию из плана перевозок. 



Экономическая постановка ТЗ
Требуется составить план перевозок продукции от поставщиков к потребителям так, чтобы
потребности потребителей были бы удовлетворены за счет вывоза запаса от поставщиков.
Цель - минимизация суммарной стоимости всех перевозок.
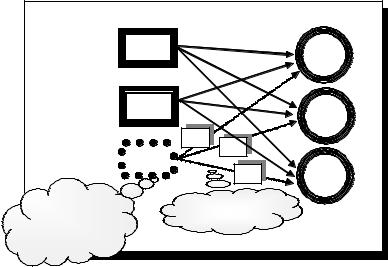
Итак, мы привели экономическую постановку транспортной задачи. Отметим один существенный момент. Если суммарный запас продукции, имеющейся у поставщиков,
совпадает с суммарной потребностью в продукции у потребителей, тогда транспортная задача считается закрытой (имеет место баланс запасов и потребностей). Если же баланс нарушается (не хватает запасов, или запасов излишек) задача называется открытой. Имея в виду тот факт, что метод потенциалов “работает” только для закрытых ТЗ, изложим способ сведения открытой ТЗ к закрытой. Суть этого способа очень проста. Так, например, при
нехватке запасов вводят в рассмотрение фиктивного поставщика с запасом, равным этой нехватке, и устанавливают цену перевозки от него к каждому потребителю (на фиктивных коммуникациях) равной нулю (самый выгодный поставщик!). Так ,в приведенном примере суммарный запас равен
120 + 70 = 190 ед. С другой стороны суммарная потребность составляет
60 + 100 + 80 = 240 ед.
|
|
39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача открытая. Имеет место нехватка |
|||||||
|
|
|
|
продукции в количестве 240 - 190 = 50 |
|||||||
120 |
|
60 |
|
ед. Вводим фиктивного поставщика с |
|||||||
|
|
|
таким запасом. Проводим от него |
||||||||
|
|
|
|
||||||||
|
|
|
|
фиктивные |
|
коммуникации |
|
ко |
всем |
||
70 |
|
100 |
|
потребителям и устанавливаем на них |
|||||||
|
|
нулевые цены. ТЗ становится закрытой. |
|||||||||
|
|
|
|||||||||
|
|
|
|
||||||||
|
0 |
|
|
Аналогично, |
при |
излишке |
запасов |
||||
|
0 |
|
|
||||||||
|
|
|
вводится |
фиктивный |
потребитель, |
||||||
50 |
|
80 |
|
||||||||
|
0 |
|
имеющий потребность, |
равную |
этому |
||||||
|
|
|
|
||||||||
Это |
Это его |
|
|
излишку. |
|
Цены |
на |
фиктивных |
|||
|
|
коммуникациях, идущих к нему от всех |
|||||||||
фиктивный |
коммуникации |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
поставщик |
|
|
|
поставщиков, |
устанавливаются |
||||||
|
|
|
|
равными нулю. |
|
|
|
|
|
||
|
|
|
|
Несколько слов об истолковании |
|||||||
решения открытой ТЗ. Пусть в оптимальном плане перевозок потребитель получает часть |
|||||||||||
продукции от “настоящих” поставщиков, а часть от фиктивного. Тогда последняя |
|||||||||||
представляет собой ту часть его потребностей, которая не удовлетворяется (недопоставка |
|||||||||||
продукции). В задаче же с излишком запасов та часть продукции, которая вывозится к |
|||||||||||
фиктивному потребителю, есть ни что иное, как продукция, остающаяся у поставщика |
|||||||||||
невывезенной |
|
|
|
|
|
|
|
|
|
|
|
В дальнейшем будем рассматривать только закрытые ТЗ. |
|
|
|
|
|
|
|
||||
Построим математическую модель ТЗ в виде задачи линейного программирования. |
|||||||||||
Исходя из того, что план перевозок определяется указанием количества перевозимого груза |
|||||||||||
по каждой коммуникации (нулевое количество, если продукция по коммуникации не |
|||||||||||
перевозится), обозначим через |
неизвестные |
xij |
количество |
перевозимой |
продукции от |
||||||
поставщика с номером i к потребителю с номером j (объем перевозки). В нашем примере |
|||||||||||
таких неизвестных будет 3х3=9 ( x11 , x12 , x13 , x21 , x22 , x23 , x31 , x32 , x33 ). В общем случае |
|||||||||||
количество неизвестных будет равно m x n, где m - количество поставщиков, n - количество |
|||||||||||
потребителей. |
|
|
|
|
|
|
|
|
|
|
|
Выразим через введенные неизвестные суммарную стоимость перевозок в виде |
|||||||||||
линейной функции. Для этого необходимо объем перевозки на каждой коммуникации |
|||||||||||
умножить на цену перевозки и просуммировать полученные величины по всем |
|||||||||||
коммуникациям. Для нашего примера имеем |
|
|
|
|
|
|
|
|
|
||
f = 5x11 |
+ 10x12 + 12x13 |
+ 8x21 + 6x22 + 4x23 |
+ 0x31 + 0x32 |
+ 0x33 → min |
|
|
|
|
|||
или, используя знаки суммирования, |
|
|
|
|
|
|
|
|
|
||
3 |
3 |
f = ∑∑cij xij → min |
|
i=1 |
j=1 |
(цель задачи - найти минимум суммарной стоимости перевозок). Здесь cij - элементы матрицы стоимостей С
|
5 |
10 |
12 |
|
C = |
8 |
6 |
4 |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
||
(При суммировании сначала изменяются индексы (номера) у внутренней суммы при фиксированном индексе у внешней суммы, затем изменяется на единицу индекс внешней суммы).
